15.3 Enthalpy of formation
The systems we have worked with until now have been of fixed
chemical composition. Because of this, we could use thermodynamic
properties relative to an arbitrary base, since all comparisons
could be made with respect to the chosen base. For example, the
specific energy
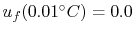 for steam. If there are no
changes in composition, and only changes in properties of given
substances, this is adequate. If there are changes in composition,
however, we need to have a reference state so there is consistency
for different substances.
for steam. If there are no
changes in composition, and only changes in properties of given
substances, this is adequate. If there are changes in composition,
however, we need to have a reference state so there is consistency
for different substances.
The convention used is that the reference state is a temperature of
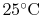 (
(
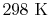 ) and a pressure of
) and a pressure of
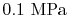 . (These are roughly room conditions.) At these
reference conditions, the enthalpy of the elements (oxygen,
hydrogen, nitrogen, carbon, etc.) is taken as zero.
. (These are roughly room conditions.) At these
reference conditions, the enthalpy of the elements (oxygen,
hydrogen, nitrogen, carbon, etc.) is taken as zero.
The results of a combustion process can be diagrammed as in
Figure 15.1. The reactants enter at standard
conditions; the combustion (reaction) takes place in the volume
indicated. Downstream of the reaction zone there is an appropriate
amount of heat transfer with the surroundings so that the products
leave at the standard conditions. For the reaction of carbon and
oxygen to produce 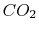 , the heat that has to be extracted is
, the heat that has to be extracted is
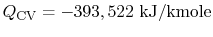 ; this is heat that
comes out of the control volume.
; this is heat that
comes out of the control volume.
Figure 15.1:
Constant pressure combustion
|
|
There is no shaft work done in the control volume and the first law
for the control volume (SFEE) reduces to:
We can write this statement in the form
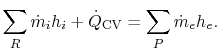 |
(15..1) |
In Eq. (15.1) the subscripts ``R'' and ``P'' on the
summations refer to the reactants (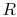 ) and products (
) and products (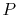 )
respectively. The subscripts on the mass flow rates and enthalpies
refer to all of the components at inlet and at exit.
)
respectively. The subscripts on the mass flow rates and enthalpies
refer to all of the components at inlet and at exit.
The relation in terms of mass flows can be written in molar form,
which is often more convenient for reacting flow problems, by using
the molecular weight, 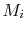 , to define the molar mass flow rate,
, to define the molar mass flow rate,
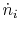 , and molar enthalpy,
, and molar enthalpy,
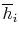 , for any
individual ith (or eth)
component as
, for any
individual ith (or eth)
component as
The SFEE is, in these terms,
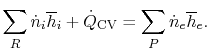 |
(15..2) |
The statements that have been made do not necessarily need to be
viewed in the context of flow processes. Suppose we have one unit of
 and one unit of
and one unit of  at the initial conditions and we carry out
a constant pressure reaction at ambient pressure,
at the initial conditions and we carry out
a constant pressure reaction at ambient pressure,
 .
If so,
.
If so,
since
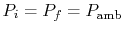 . Combining terms,
. Combining terms,
or
In terms of the numbers of moles and the specific enthalpy this is
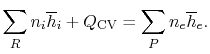 |
(15..3) |
The enthalpy of  , at
, at
 and
and
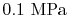 , with reference to a base where the enthalpy of the elements
is zero, is called the enthalpy of formation and denoted by
, with reference to a base where the enthalpy of the elements
is zero, is called the enthalpy of formation and denoted by
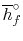 . Values of the heat of formation for a number
of substances are given in Table A.9 in SB&VW.
. Values of the heat of formation for a number
of substances are given in Table A.9 in SB&VW.
The enthalpies of the reactants and products for the formation of
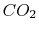 are:
are:
The enthalpy of 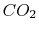 in any other state
in any other state 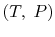 is
given by
is
given by
These descriptions can be applied to any compound. For elements or
compounds that exist in more than one state at the reference
conditions (for example, carbon exists as diamond and as graphite),
we also need to specify the state.
Note that there is a minus sign for the heat of formation. The heat
transfer is out of the control volume and is thus negative by
our convention. This means that
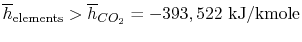 .
.
Muddy Points
Is the enthalpy of formation equal to the heat transfer out of the
combustion during the formation reaction?
(MP 15.4)
Are the enthalpies of 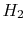 and
and 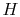 (monoatomic hydrogen) both zero
at
(monoatomic hydrogen) both zero
at
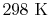 ? (MP 15.5)
? (MP 15.5)
UnifiedTP
|


![]() are:
are:
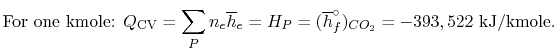
![]() .
.
![]() and
and ![]() (monoatomic hydrogen) both zero
at
(monoatomic hydrogen) both zero
at
![]() ? (MP 15.5)
? (MP 15.5)