

|
|
| Thermodynamics and Propulsion | |
An ideal thermal radiator is called a ``black body.'' It has several
properties:
|
|
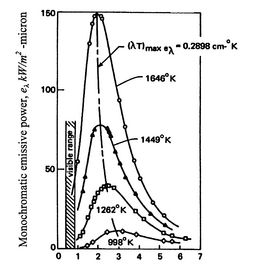
The distribution of ![]() varies with temperature. The
quantity
varies with temperature. The
quantity ![]() at the condition where
at the condition where ![]() is a maximum
is given by
is a maximum
is given by
![]() . As
. As ![]() increases, the wavelength for maximum energy emission
shifts to shorter values. The frequency of the radiation,
increases, the wavelength for maximum energy emission
shifts to shorter values. The frequency of the radiation, ![]() , is
given by
, is
given by
![]() so high energy means short wavelengths and
high frequency.
so high energy means short wavelengths and
high frequency.
A physical realization of a black body is a cavity with a small hole (Figure 19.3). There are many reflections and absorptions. Very few entering photons (light rays) will get out. The inside of the cavity has radiation which is homogeneous and isotropic (the same in any direction, uniform everywhere).
Suppose we put a small black body inside the cavity as seen in Figure 19.4. The cavity and the black body are both at the same temperature.
The radiant energy absorbed by the black body per second and per
m2 is
![]() , where
, where ![]() is the irradiance,
the radiant energy falling on any surface inside the cavity. The
radiant energy emitted by the black body is
is the irradiance,
the radiant energy falling on any surface inside the cavity. The
radiant energy emitted by the black body is ![]() . Since
. Since
![]() for a black body,
for a black body, ![]() . The irradiance within a cavity whose
walls are at temperature
. The irradiance within a cavity whose
walls are at temperature ![]() is therefore equal to the radiant
emittance of a black body at the same temperature and irradiance is
a function of temperature only.
is therefore equal to the radiant
emittance of a black body at the same temperature and irradiance is
a function of temperature only.
UnifiedTP