8.6 Enhancements of, and Effect of Design Parameters on, Rankine
Cycles
The basic Rankine cycle can be enhanced through processes such as
superheating and reheat. Diagrams for a Rankine cycle with
superheating are given in Figure 8.13. The
heat addition is continued past the point of vapor saturation, in
other words the vapor is heated so that its temperature is higher
than the saturation temperature associated with
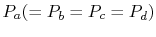 . This does several things. First, it increases the mean
temperature at which heat is added,
. This does several things. First, it increases the mean
temperature at which heat is added, 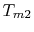 , thus increasing the
efficiency of the cycle. Second is that the quality of the two-phase
mixture during the expansion is higher with superheating, so that
there is less moisture content in the mixture as it flows through
the turbine. (The moisture content at
, thus increasing the
efficiency of the cycle. Second is that the quality of the two-phase
mixture during the expansion is higher with superheating, so that
there is less moisture content in the mixture as it flows through
the turbine. (The moisture content at 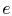 is less than that at
is less than that at
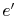 .) This is an advantage in terms of decreasing the mechanical
deterioration of the blading.
.) This is an advantage in terms of decreasing the mechanical
deterioration of the blading.
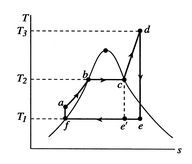
Figure 8.13:
Rankine cycle with superheating
[ 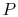
- 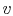
coordinates]
[ 
- 
coordinates]
[ 
- 
coordinates]
|
The heat exchanges in the superheated cycle are:
- Along
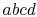 , which is a constant pressure (isobaric) process:
, which is a constant pressure (isobaric) process:
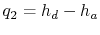 .
.
- Along
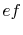 :
:
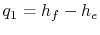 ,
, 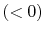 .
.
The thermal efficiency of the ideal Rankine cycle with superheating
is
This can be expressed explicitly in terms of turbine work and
compression (pump) work as
Compared to the basic cycle, superheating has increased the turbine
work, increased the mean temperature at which heat is received,
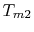 , and increased the cycle efficiency.
, and increased the cycle efficiency.
Figure 8.14:
Comparison of Rankine
cycle with superheating and Carnot cycle
|
|
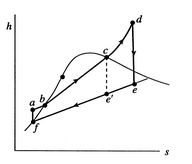
Figure 8.15:
Rankine cycle with superheating
and reheat for space power application
|
|
A comparison of the Carnot cycle and the Rankine cycle with
superheating is given in Figure 8.14.
The maximum and minimum temperatures are the same, but the average
temperature at which heat is absorbed is lower for the Rankine
cycle. To alleviate the problem of having moisture in the turbine,
one can heat again after an initial expansion in a turbine, as shown
in Figure 8.15, which gives a schematic of a
Rankine cycle for space power application. This process is known as
reheat. The main practical advantage of reheat (and of superheating)
is the decrease in moisture content in the turbine because most of
the heat addition in the cycle occurs in the vaporization part of
the heat addition process.
Figure 8.16:
Effect of exit pressure on
Rankine cycle efficiency
|
|
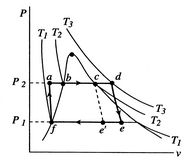
We can also examine the effect of variations in design parameters on
the Rankine cycle. Consider first the changes in cycle output due to
a decrease in exit pressure. In terms of the cycle shown in
Figure 8.16, the exit pressure would
be decreased from 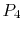 to
to 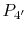 . The original cycle is
. The original cycle is
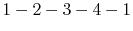 , and the modified cycle is
, and the modified cycle is
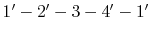 . The consequences
are that the cycle work, which is the integral of
. The consequences
are that the cycle work, which is the integral of 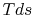 around the
cycle, is increased. In addition, as drawn, although the levels of
the mean temperature at which the heat is absorbed and rejected both
decrease, the largest change is the mean temperature of the heat
rejection, so that the thermal efficiency increases.
around the
cycle, is increased. In addition, as drawn, although the levels of
the mean temperature at which the heat is absorbed and rejected both
decrease, the largest change is the mean temperature of the heat
rejection, so that the thermal efficiency increases.
Figure 8.17:
Effect of maximum boiler
pressure on Rankine cycle efficiency
|
|
Another design parameter is the maximum cycle pressure.
Figure 8.17 shows a comparison of two
cycles with different maximum pressure but the same maximum
temperature, which is set by material properties. The average
temperature at which the heat is supplied for the cycle with a
higher maximum pressure is increased over the original cycle, so
that the efficiency increases.
Muddy Points
Why do we look at the ratio of pump (compression) work to turbine
work? We did not do that for the Brayton cycle.
(MP 8.10)
Shouldn't the efficiency of the super/re-heated Rankine cycle be
larger because its area is greater?
(MP 8.11)
Why can't we harness the energy in the warm water after condensing
the steam in a power plant?
(MP 8.12)
UnifiedTP
|

