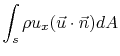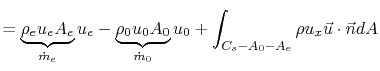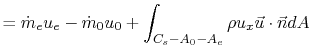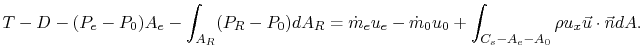10.3 Application of the Momentum Equation to an Aircraft Engine
Consider the jet engine shown in Figure 10.4.
Figure 10.4:
Control volume for application of momentum theorem to an
aircraft engine
|
|
So we have:
Everything that relates to flow through the
engine is conventionally called thrust. Everything that relates to
the flow on the outside of the engine is conventionally call drag.
Therefore, gathering only those terms that relate to the fluid that
passes through the engine, we have:
The thrust is largely composed of the net change in momentum of the
air entering and leaving the engine, with a typically small
adjustment for the differences in pressure between the inlet and the
exit. We could have arrived at the same equation by considering only
the streamtube that passes through the engine as shown in
Figure 10.5.
Note that the static pressure along the curved control surfaces is different from ambient pressure due to streamline curvature.
Figure 10.5:
Alternate control volume for
application of momentum theorem to an
aircraft engine
|
|
UnifiedTP
|


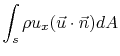
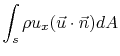
![$\displaystyle = T-D+\left[-P_e A_e + P_0 A_e - \int_{A_R} (P_R-P_0)dA_R\right]$](img1232.png)