13.2 Power Required
Now we can look at the
propulsion system requirements to maintain steady level flight since
and
Thus the power required (for steady level flight) takes the form of
Figure 13.3.
Figure 13.3:
Typical power required curve for an aircraft.
|
|
The velocity for minimum power is obtained by taking the derivative
of the equation for
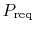 with respect to
with respect to 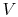 and
setting it equal to zero.
and
setting it equal to zero.
As we will see shortly, maximum endurance (time aloft) occurs
when the minimum power is used to maintain steady level flight.
Maximum range (distance traveled) is obtained when the
aircraft is flown at the most aerodynamically efficient condition
(maximum 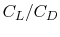 ).
).
UnifiedTP
| 

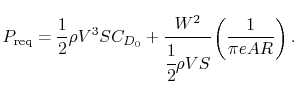
![]() with respect to
with respect to ![]() and
setting it equal to zero.
and
setting it equal to zero.
![$\displaystyle V_{\textrm{minimum power}} = \left[\frac{4}{3}\left(\frac{W}{S}\r...
...}{\rho^2}\frac{1}{C_{D_0}}\left(\frac{1}{\pi e AR}\right)\right]^{\frac{1}{4}}.$](img1599.png)