Assignment 1
MPI
Due: Tuesday, February 20, 1996
The purpose of this assignment is
to jump right in and learn how
to write message passing code with
the message passing interface
language
MPI .
My suggestion is install MPI, and run
the pi computation program before reading
the manuals. If you are determined to,
you can buy the MPI book
Using MPI which is available from
MIT press. I suspect it may be purchased at the
COOP and the MIT Press
bookstore, but call ahead and ask.
(If somebody does this, let me know, and I will post.)
It is not necessary to purchase the book,
a good first step would be to see if you can
understand or guess at what is probably
going on in the example
Fortran program or
C program
to compute pi by integrating
f(x)= 4/(1+x^2) from 0 to 1.
If you are willing to understand most, but
not all, of the code, you will probably make
very fast progress. The next step
is to execute the code (see below), and the third
step is to make sure you understand it
by playing with the code, and perhaps
reading some of the
tutorials.
The
tutorial
by Peter Pacheco looks like a particularly good one.
You can also lookup individual commands
in the index .
If you like, we can arrange to do all this together
in an electronic classroom some evening just
to see how it all goes and avoid time wasting
systems problems.
1) Obtaining an MPI for yourself:
If your department has a network of workstations
such as the unix workstations in the mathematics
department, it is fun to install MPI yourself.
One easy choice (I tried it myself) is the
easy eight step (actually just do steps
one through seven unless you have root password)
quick start to loading the free and well written
MPICH (MPI chameleon)
package from Argonne National Lab.
(The origin of the name
chameleon goes back to an old portable message
passing system from Argonne that predates
MPI.)
The benefits of using this program is that
it works. The only drawback is that
vendor supplied implementations for special
machines should be faster.
If you are using a Sun network, step 4 of the
eight steps is exactly correct.
On another network, you probably would
want to change the -arch
argument, but I think the -device=ch_p4
works just fine.
If you want
to use two machines with different filesystems
one way is to use the -p4pg pgfile
switch as described in
the fourth paragraph of the
section entitled
"Heterogeneous networks and closer control"
of the
MPICH Users Guide.
An example pgfile that worked
between the mathematics department and
the theory group over at the Lab for Computer
Science looks like this (processor0 in math),
(processor 1 at LCS)
weierstrass 0 /tmp_mnt/home/b2/edelman/mpi/mpich/examples/basic/cpi
woodpecker.lcs.mit.edu 1 /c/edelman/mpi/mpich/examples/basic/cpi
Keep me posted to other things that you try either out
of necessity or curiosity.
If you find that you have devoted more than one
hour to this project, stop, give up, and send
me email. It is not worth your time.
I am getting you all accounts on the IBM SP-2 (sp2.mit.edu)
and the SGIs.
There MPI is already installed.
I just ran the SP-2 code myself
thanks to help from Sivan Toledo.
sp2.mit.edu doubles as node9. Please consider randomly logging
onto sp2n10, sp2n11, and sp2n12 also.
2) Run the c or Fortran pi program.
First do it on one processor, then on
(P=)
two, three, or four processors. Edit the code
so that it takes smaller rectangles.
Get some timings for different deltas
on P processors and on one processor.
Compare the former with the latter
divided by P on a graph. What conclusion
can be reached?
3) Write a program to sum P numbers,
where P is an arbitrary power of 2.
For simplicity place the single
number i on processor i and form
the binary tree that would add these
numbers. (Of course nobody would
ever compute with one number per processor).
Use send and receives. (Is blocking or non-blocking better?)
(I think I like the
introductory tutorial on point to point communication
from Cornell.)
The program should have a loop with
exactly log2(P) steps.
There should be no unnecessary communication.
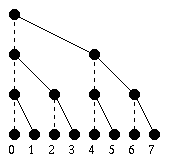
The diagram below illustrates the computation
on eight processors
with communication shown in heavy lines.
The inner loop consists of a
send, a receive, and a sum. This loop
is executed three times when there are
eight processors.
4) Continuing with problem 3, rather than broadcasting, the sum
to every processor, pass the sum back
down the leaves of the binary tree
using sends and receives.
Again there should be log2(P) steps and
no unnecessary communication.
The diagram above may be used again, but
this time the communication occurs
"down" the tree.
5) This is the most difficult problem.
It may seem artificial for now, but later
in the course, you will see why this
is exactly a simplification of
the multipole algorithm.
Assume the data structure from problem 3
is intact. In other words, assume the
binary tree consisting of all the partial
sums is still available. For example,
if there are eight processors, there
should be four partial sums on processor 0,
two on processor 2, and three on processor 4
in memory.
Here is your goal. Each
processor must compute the sum of all
of the numbers except for itself and its (at most) two neighbors.
Therefore processor 3 computes the sum of all the numbers
except those in processors 2, 3, and 4. Processor 0
computes the sum of the numbers in processors 2, 3, 4, ....
The catch is that I want you to compute this in a very
special way. You might find this way silly at first,
but there is an important pedagogical reason I want you to do it
this way. Rather than beginning by defining what I want,
let me show what will happen in processor 8 in a 32 processor
system:
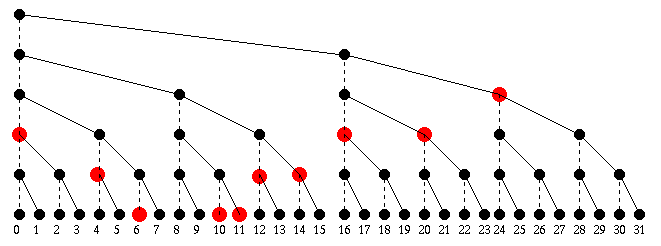
From the point of view of processor 8, the first
thing that happens is processor 24 sends over
the sum of the numbers from p24 to p31.
(Notice the communications lines do not respect
the tree stucture, i.e. in this example processor 24
is talking to processor 8 even though no line exists.)
On the next step, this is added to the values in p0,
p16 and p20. On the third step, the preceding
sum is added to the values from p4, p12 and p14.
Finally on the last step, p8 gets and adds in
the values in p6, p10, and p11. When the computation
is done, p8 has the sum of all the numbers except
for those from p7, p8, and p9.
How may this be described? What is happening is
that in this top to bottom calculation, p8 is
receiving as much as it can without loading
in information from itself nor from the nearest
neighbor at that level.
For example, consider the level containing p0, p4,
p8, p12, p16, p20, p24, and p28.
We do not wish to include information from p8, nor
the two nearest neighbors p4 and p12. Also we already
have the information from p24 and p28 from the previous
step of the calculation. Note: you are allowed to
inherit your parent's other sum information, for
example, at the first step, P0 gets information from
P24, at the second step, P4 can get *this* information
from P0.
Your job is to write code that is executed on
each processor that simultaneously does this
computation for each processor.
You may wish to use MPI_sendreceive
Programming style matters. The code should
be a loop with almost log2(p) iterations, and the
loop (except for the first iteration)
should consist of an inheritance of a partial
sum from a parent (that does not include itself)
and
three MPI_sendreceive
calls which are functions of the processor number.
The code should be general enough to work on
an arbirary power of 2 number of processors.
Neatness and style count.
If you don't have a large number of processors,
you may simulate having more processors by having
multiple processes per processor. If you are using
mpich this may be done by repeating
node names multiple times.
Back to the class home page.


