| |
|
|||||||
| |
||||||||
| |
|
|
|
|
|
|
||
| |
||||||||
|
|
|
|
|
||||||
|
|
Problem 5.02: Force on a fireman's hose | |
|
||||||
|
|
|
|
|
|
|
We are interested
in how the shape of the nozzle and the direction of the stream affects the
force required to hold a fireman's hose. The sketch shows a test rig where
a hose-nozzle combination is held firmly by a support. The bellows transmits
no force to the parts mounted on the support (the hose to the left of it
is supported separately). Water is supplied at a volume flow rate Q (m
3s-1)via
a horizontal hose of radius R1, the flow within being in the
x-direction, to a nozzle with a smaller exit radius R2
and an outward normal vector  . The
coordinates are indicated in the figure. The nozzle exit plane is at an
elevation h relative to the horizontal supply
hose, where y=0. The density of water is r, and the atmospheric
pressure is pa. The weight of material (water, hose, and nozzle)
between the bellows and the nozzle's exit plane is W. |
|
|
|
|
(a) Assuming
that the flow between stations 1 and 2 is incompressible and inviscid, derive
an expression for the force 
exerted on the fire-hose by the support. Write
the answer in terms the given quantities
|
|
|
|
|
 |
|
|
|
|
 |
|
|
|
|
 |
|
|
|
|
 |
|
|
|
|
(b)
Demonstrate that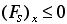 
always, that is, in order to hold the system
in place, one must always push on it toward the left, regardless of volume
flow rate or angle.
(c) For the simple case Q=0 (no flow, but system filled with static liquid to height h), our answer predicts that the external force required to hold it in place is
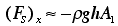
Consider a system mounted on a support with frictionless wheels. The result (1) suggests that if such a system is held in place and filled with water, and the external holding force removed, it will tend to move to the right. Does this make sense? Explain. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
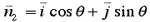(d) Now consider another special case: a straight
horizontal pipe, that is,
regardless of the shape of the system between 1 and 2. Explain on physical grounds why this makes sense. |
|
|
|
|
|
|
|
|
|
|
|
|
.
