|
Sluice gates are used to regulate water level
(or flow rate) in open channels. The figure shows a gate that is adjusted
so that the upstream depth is maintained at a depth h1.
The density of water is r, and the acceleration
of gravity is g. The water flow
under the gate may be considered incompressible and inviscid.
Suppose the downstream depth is measured as
h2, that is, the quantities
h1, h2,
r, and g are
known.
(a) Assuming uniform velocities at the far
upstream and downstream stations1 and 2 derive an expression for the
horizontal force F, per unit breadth, required to hold the gate
in place. Check your result by showing that it gives zero when h1=h2
and the hydrostatic result 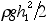 when h2=0. when h2=0.
|
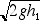 .
Explain.
.
Explain.