A 2D Incompressible Navier-Stokes Solver Using the Finite Volume Method Implemented in C++
by Maytee Chantharayukhonthorn
Developed a 2D Incompressible Navier-Stokes Solver Using the Finite Volume Method Implemented in C++ and benchmarked against common flows like the lid-driven cavity flow and flow around a cylinder.
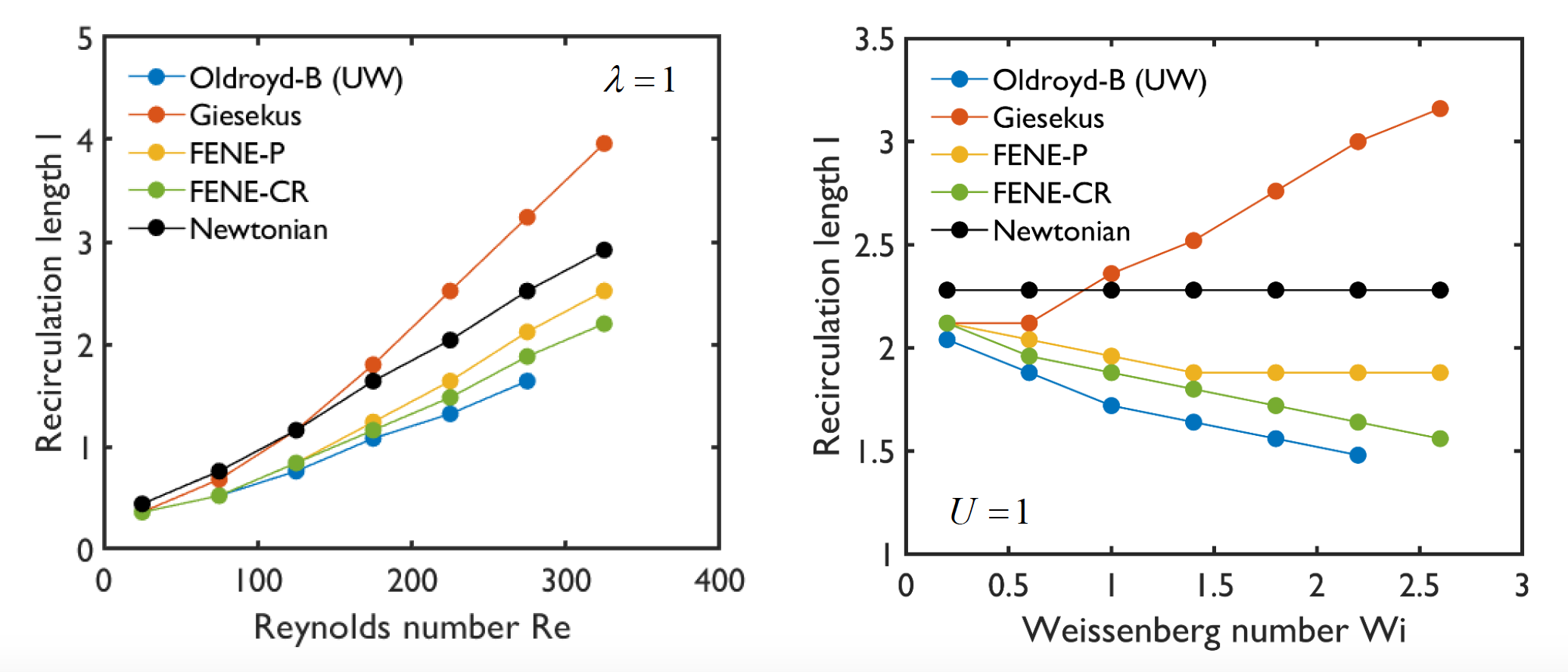
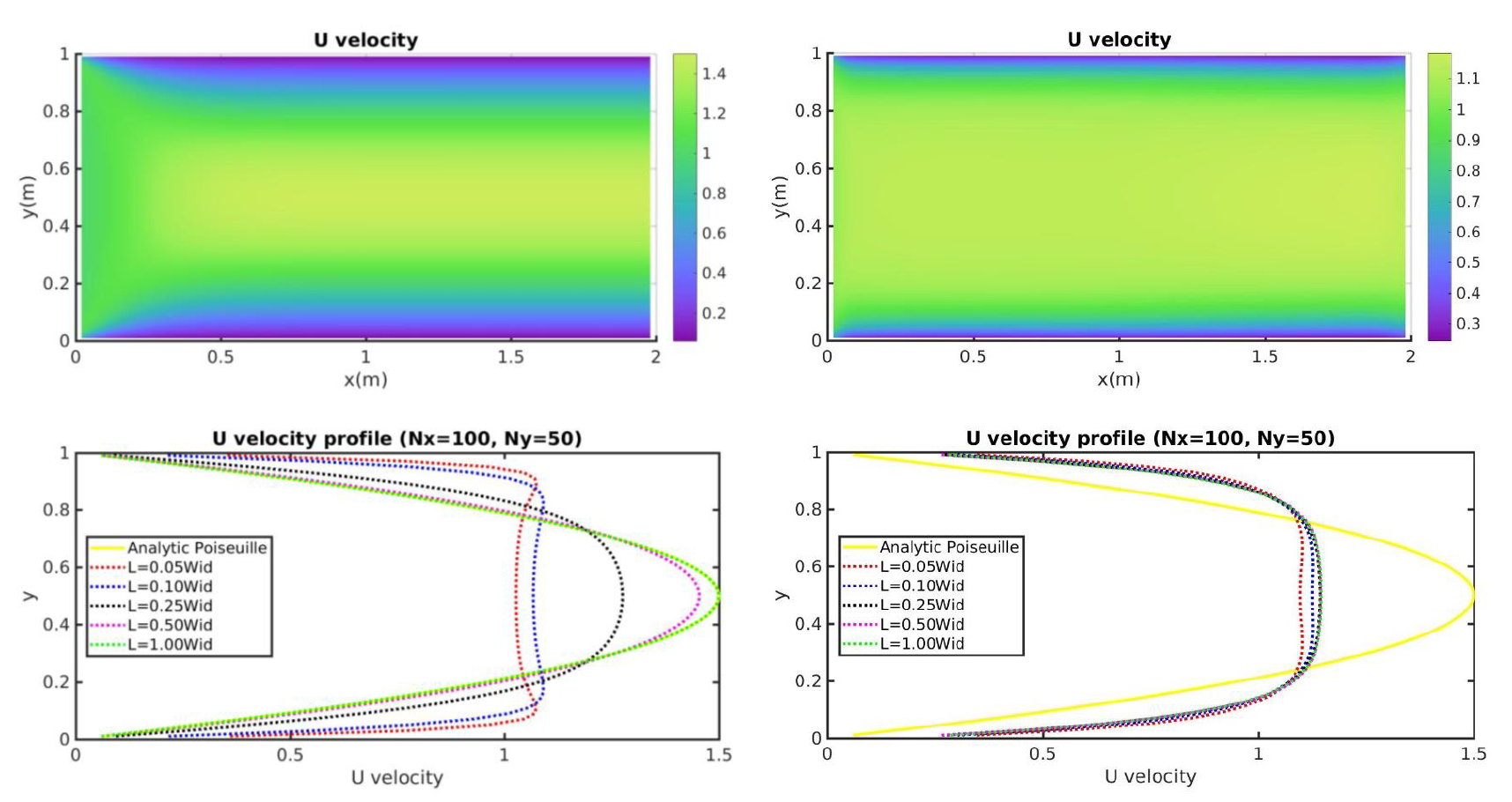
In this project, I attempt to modify the deterministic NS solver provided as part of the 2.29 finite volume framework to simulate simple, unsteady flows of non-Newtonian polymer solutions. Specifically, the Newtonian constitutive equation is replaced with the Oldroyd-B model, which is the simplest rheologically admissible (quasilinear) model available for polymer solutions and melts. I will also attempt to simulate flows in simple two-dimensional geometries, and compare the results to benchmark solutions in the literature. Issues with convergence at large Weissenberg numbers will also be studied.
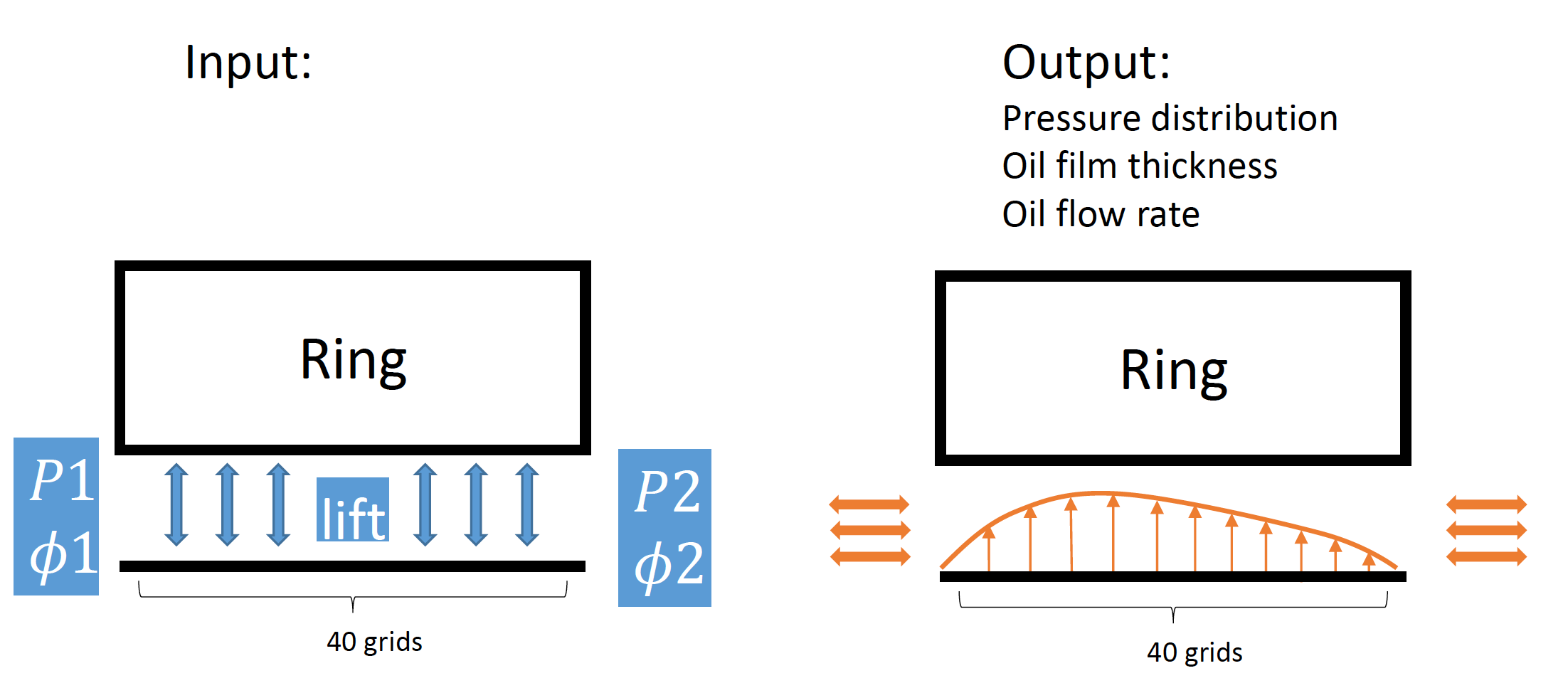
Developing a pumping model for piston ring-groove oil/air transportation in an IC engine
by Wang Zhang
My current research is about developing a 3D ring dynamics model describing piston ring and gas/oil flow behaviors in IC engine systems. It consists of a finite element model of the ring and several sub- models describing the ring interaction with engine systems (liner, groove, gas, oil). For ring-groove oil/gas flow, we are now using a pressure driven model which is simple and robust while unable to describe the suction effect within the area. To overcome this issue, we need to derive a new model for to describe the physical phenomenon and maintain calculation simplicity.

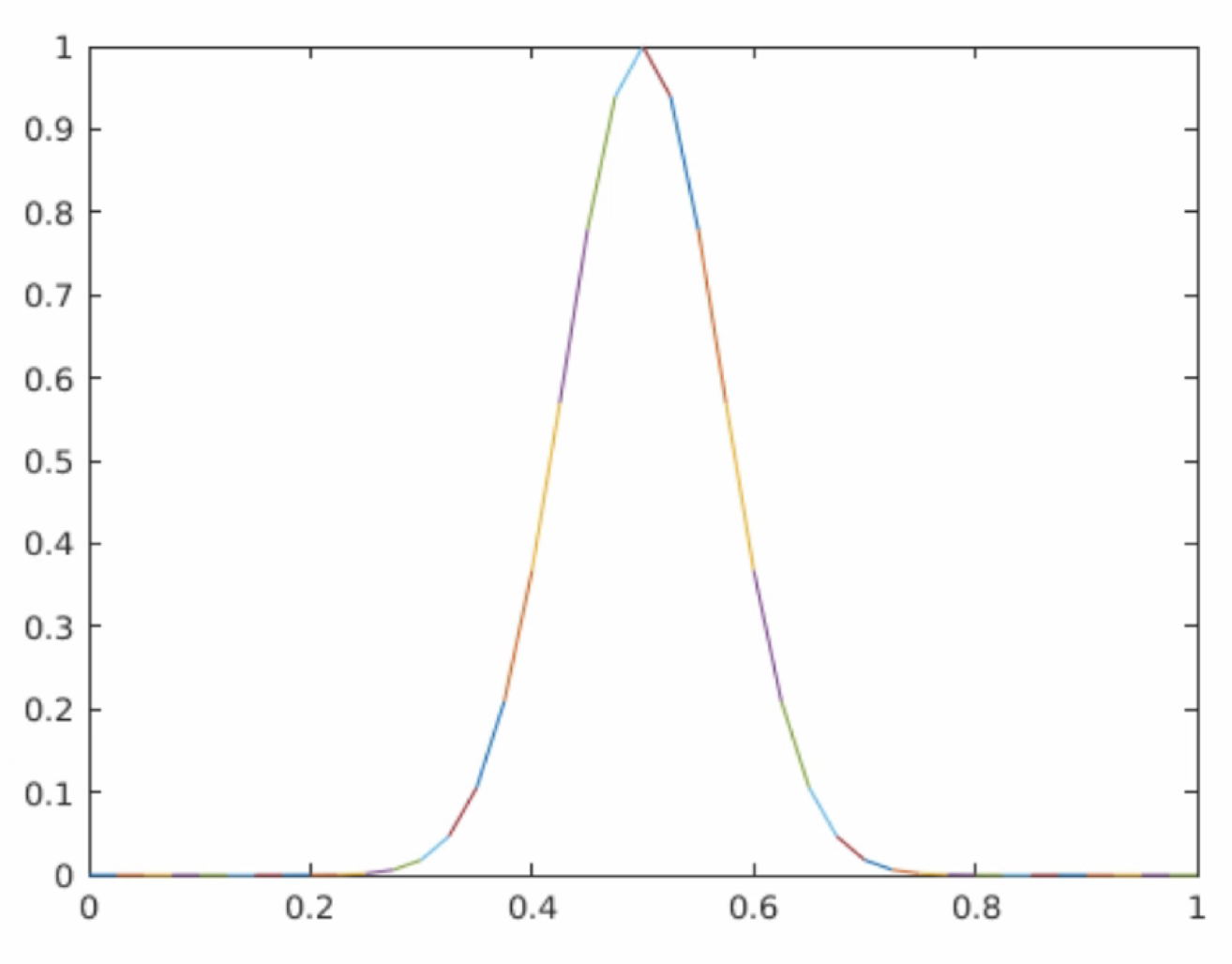
In my project, I will be studying soliton solutions (in 1D) and their behavior, subject to the KdV equation. I will be looking at interesting behaviors associated with the “stationary” behavior of single solitons, the interaction between two solitons, and perhaps even showing how more powerful non-solitary waves “decay” into a train of solitary solutions. Mostly, this project will involve implementing a few different finite difference/volume methods and confirming that their rates of convergence are as expected.
A 3D sharp interface method for modelling the mixing of two partially miscible fluid phases
by Aniket Sanjay Patankar
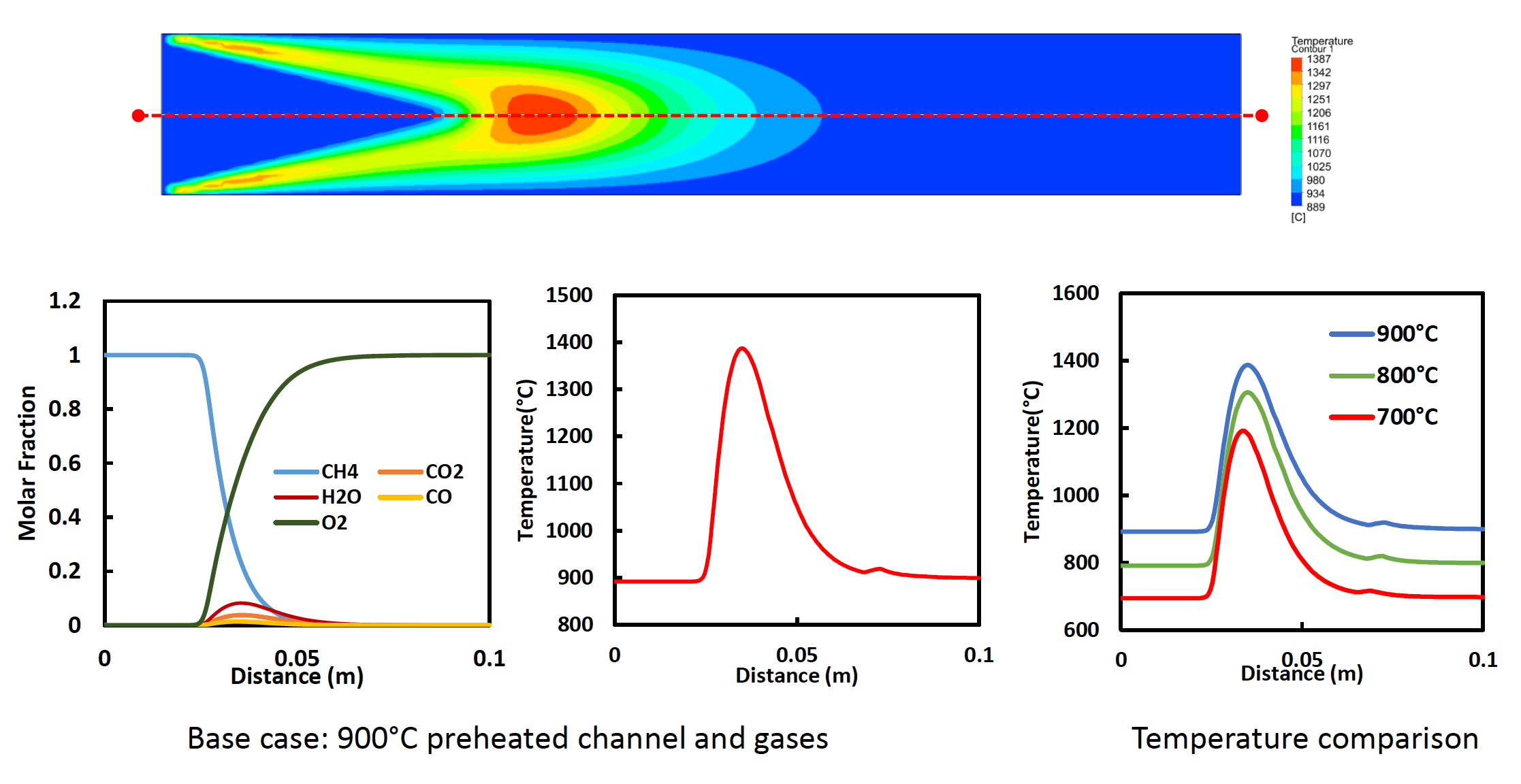
"I am reviewing a code developed in the RGD lab at MIT to model the mixing of heavy oil and supercritical water. The code has been developed by Ashwin Raghavan, Dr. Ping He and Prof. Ahmed Ghoniem. Key features of this code include: 1. The code uses a geometric advection algorithm to track the evolution of a sharp phase interface in time. The PLIC interface reconstruction method has been used. 2. Handling species diffusion between arbitrarily shaped cells (specifically involving cells containing the phase interface) 3. Strong coupling of interfacial mass transfer, species and heat diffusion, and thermodynamic equilibrium (the thermodynamics has been modelled with a cubic PPR78 equation of state). I will present the above methods in some detail, go over code validation and convergence studies, and show some sample results I obtain from running the code."
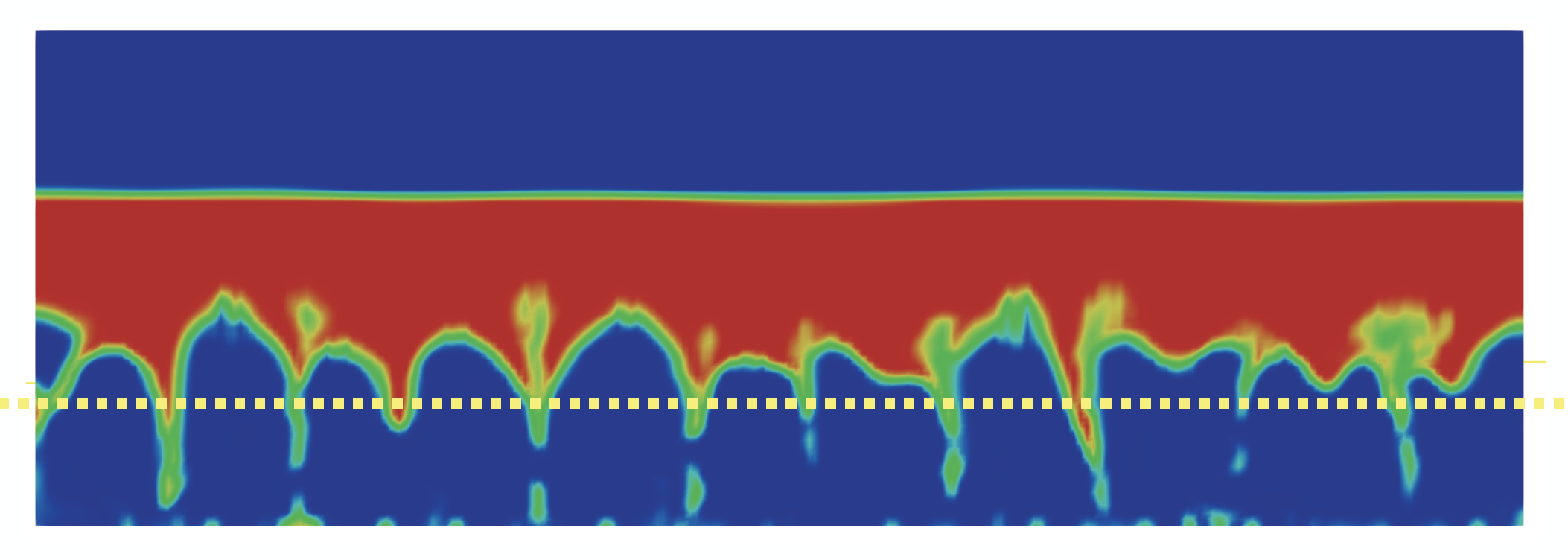
A density-driven Rayleigh-Taylor hydrodynamic instability can spontaneously develop between two miscible fluids in a Hele-Shaw geometry. Surprisingly, we find that the typically unstable interface between the inner and outer fluids is stabilized below a critical plate spacing. This plate spacing scales as a power law with the difference in density between the fluids. We find that our measured wavelength in this confined geometry deviates from theoretical predictions for unconfined systems by two orders of magnitude. I plan to simulate this system starting from the Navier-Stokes equations and Fick's law. I hope the simulation will aid in understanding this critical stabilizing spacing and its dependence (or lack thereof) on fluid parameters, the mechanism for instability growth, and compare its wavelength predictions to empirical findings.
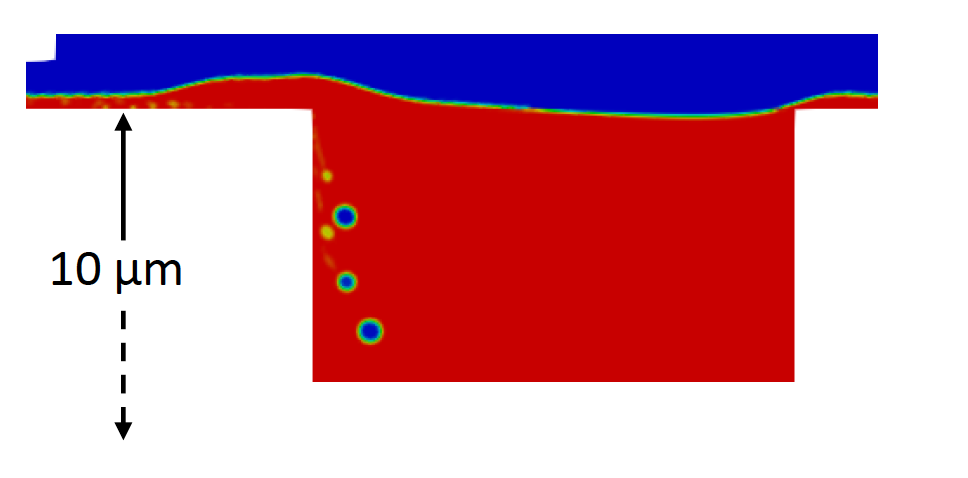
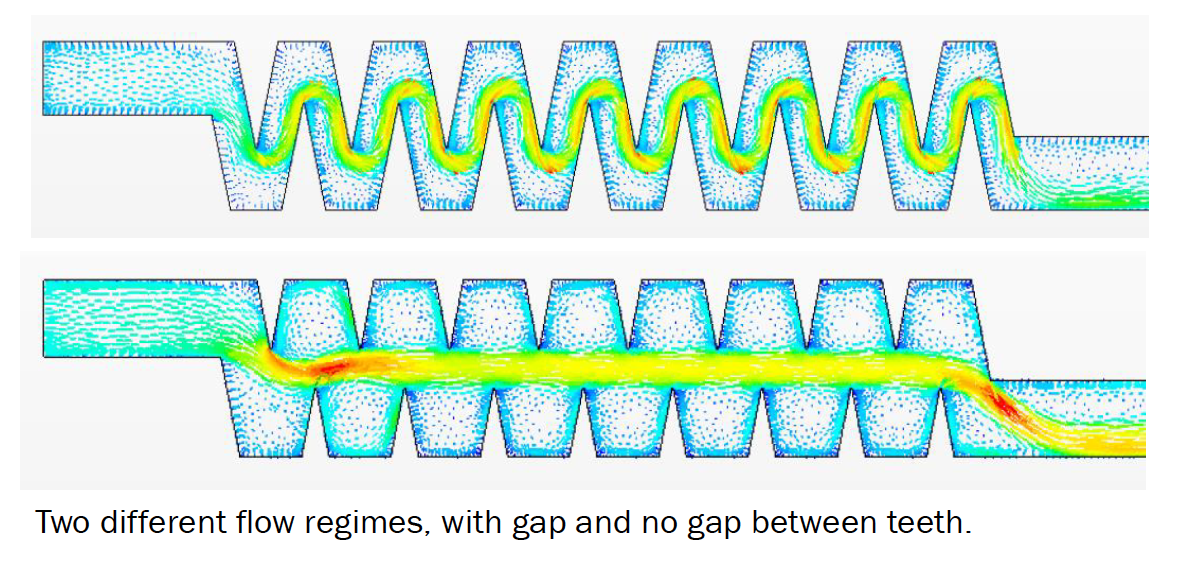
Parametric CFD-based surrogate model for pressure loss in tortuous paths of drip emitters
by Julia Sokol
The goal of this project is to obtain a quick method to calculate the pressure drop across the tortuous path of a drip irrigation emitter given a path geometry (see image of a typical emitter below), or the other way around – to determine the needed geometry of the path given a desired pressure drop. I will begin by simulating the flow in the tortuous path of an inline drip irrigation emitter in STAR-CCM+. I will compare the results of using several RANS turbulence models (standard k-epsilon, realizable k-epsilon, standard k-omega and SST (Menter) k-omega), select the most appropriate one for the application, and do a grid convergence analysis to estimate the discretization error. The base design will then be parametrized geometrically (with parameters such as tooth height, angle, spacing, etc.), and multiple simulations will be run, with parameter values set by a design of experiments algorithm. Finally, the results of the simulations (pressure drop across the tortuous path) will be compiled, and, if possible, a meta-model based on multivariate linear regression will be generated, with parameter values (or combinations of parameters) as inputs and pressure drop as the output. The accuracy and limits of applicability of the meta-model will be analyzed.
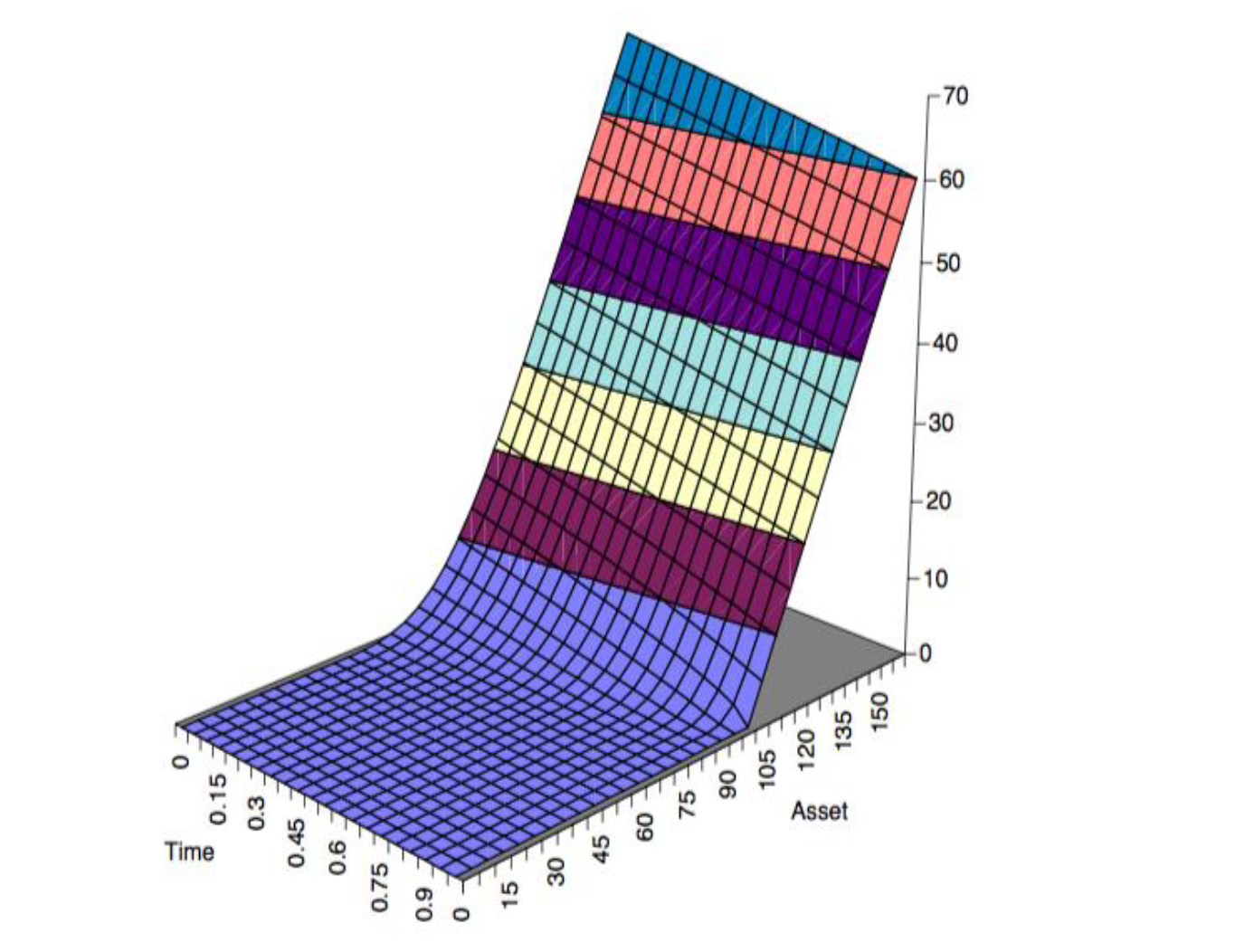
Numerical Recipes for Options Pricing: From Plain Vanilla to Complex Exotics
by Shenbo Xu