Horizontal Component Example Problem

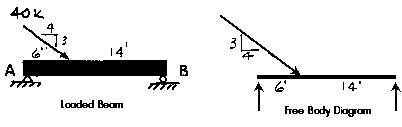
Lecture 14
Example Problem

Components of Reactions

Given:
the beam of the previous example problem with the loading modified to contain a horizontal component as seen in the figure below.
Determine:
the reactions at A and B.
Lecture 14

The horizontal component can be resisted only by the reaction at A since the support at B is a roller support. The pinned reaction at A will resist translation in any direction. The assumed reaction A is replaced by its rectangular components Ax and Ay (or AH and AV). The reaction at A is a single force; Ax and Ay represent the components of that one force.

If we do not know the direction of the force, we must assume a direction. If the assumption is correct, the answer will have a positive sign; if the assumption is incorrect, the answer will have a negative sign. Although in this case it is possible to g uess the sign of the reactions, it is not always so. Choosing "all posative"- up or to the right- minimizes possible confusion over the meaning of resulting signs.

Use the three equations of equilibrium to solve for the reactions.

Sum Fx = 0 = 4/5(40k) + Ax
Sum Fy = 0 = -3/5(40k) + Ay + B
Sum MA = 0 = 3/5(40k)(6ft) - B(20ft)

The first and third equations can be solved immediately.

Ax = -32k
B = 7.2k

Now use B = 7.2k in the second equation to solve for Ay.

Sum Fy = 0 = -24k + 7.2k + Ay
Ay = 16.8k

A can be found using the Pythagorean Theorem.

A = SQRT (-32k^2 + 16.8k^2)
A = 36k

The direction is up and to the right. The angle above the x axis equals

ø = arctan (-16.8 / 32) = 27.7 degrees

In summary, the reactions of the beam are as follows:
at A a force of 36 kips acting up and to the right at an angle of 27.7 degrees and
at B a force of 7.2k acting up.

Lecture 14 Example Problem

Lecture 14
Example Problem