Non-Concurrent, Non-Parallel Force Systems
Non-Concurrent, Non-Parallel Force Systems
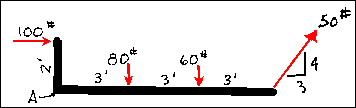The principles of equilibrium are also used to determine the resultant
of non-parallel, non-concurrent systems of forces. Simply put, all
of the lines of action of the forces in this system do not meet at one point.
The parallel force system was a special case of this type. Since all of
these forces are not entirely parallel, the position of the resultant can
be established using the graphical
or algebraic methods of resolving
co-planar forces discussed earlier or the link polygon.
There are a number of ways in which one could resolve the force system that is shown. One graphical method would be to resolve a pair of forces using the parallelogram or triangle method into a resultant. The resultant would then be combined with one of the remaining forces and a new resultant determined, and so on until all of the forces had been accounted for. This could prove to be very cumbersome if there is a great number of forces. The algebraic solution to this system would potentially be simpler if the forces that are applied to the system are easy to break into components. The algebraic resolution of this force system is illustrated in the example problem.
Algebraic Resolution of a Non-Concurrent System
The Link Polygon is a graphical method to determine the resultant of non-concurrent, non-parallel force systems. It depends on an accurate graphical representation of all of the forces acting on a system. Essentially, each of the given forces is successively replaced by two components that are arranged so that one component of the force is equal in value to a component of the succeeding force. When all of the components have been combined in this way, the remaining force is the resultant of the system. This is accomplished by having a common "polar point" within the force polygon from which the components of the forces are generated. This point can be located anywhere in space, but is often chosen so that the link polygon will fit on the free body diagram.
hmmm.....
TBA