| | The Divergence Operator |
|---|
| 2.1.1* | In Cartesian coordinates, A = (Ao /d2)(x2ix + y2 iy +
z2 iz), where Ao and d are constants. Show that div A
= 2Ao (x + y + z)/d2.
|
| 2.1.2* | In Cartesian coordinates, three vector functions are


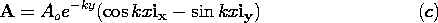 where Ao, k, and d are constants.
where Ao, k, and d are constants.
| (a) | Show that the divergence of each is zero.
|
| (b) | Devise three vector functions that have a finite
divergence and evaluate their divergences.
|
|
| 2.1.3 | In cylindrical coordinates, the divergence operator is given in
Table I at the end of the text. Evaluate the divergence of the
following vector functions.
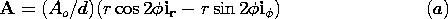
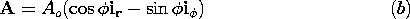

|
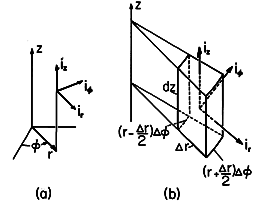
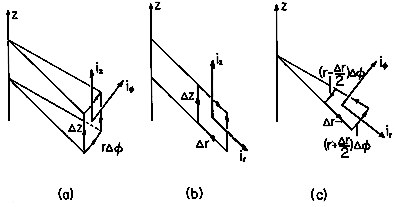
| 2.1.4* | In cylindrical coordinates, unit vectors are as defined in
Fig.~P2.1.4a. An incremental volume element having sides
( r, r r, r 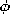 , ,  z)
is as shown in Fig.~P2.1.4b. Determine the divergence operator by
evaluating (2), using steps analogous to those leading from (3)
to (5). Show that the result is as given in Table I at the end of
the text. (Hint: In carrying out the integrations over the surface
elements in Fig.~P2.1.4b having normals z)
is as shown in Fig.~P2.1.4b. Determine the divergence operator by
evaluating (2), using steps analogous to those leading from (3)
to (5). Show that the result is as given in Table I at the end of
the text. (Hint: In carrying out the integrations over the surface
elements in Fig.~P2.1.4b having normals  ir, note that not
only is Ar evaluated at r = r ir, note that not
only is Ar evaluated at r = r  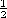  r, but so also is
r. For this
reason, it is most convenient to group Ar and r together in
manipulating the contributions from this surface.) r, but so also is
r. For this
reason, it is most convenient to group Ar and r together in
manipulating the contributions from this surface.)
|
| 2.1.5 | The divergence operator is given in spherical coordinates in Table I
at the end of the text. Use that operator to evaluate the divergence
of the following vector functions.


|
| 2.1.6* | In spherical coordinates, an incremental volume element has sides
 r, r\Delta r, r\Delta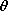 , r sin , r sin 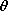 \Delta \Delta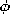 . Using
steps analogous to those
leading from (3) to (5), determine the divergence operator by evaluating
(2.1.2). Show that the result is as given in Table I at the end of
the text. . Using
steps analogous to those
leading from (3) to (5), determine the divergence operator by evaluating
(2.1.2). Show that the result is as given in Table I at the end of
the text.
|
| | Gauss' Integral Theorem |
|---|
| 2.2.1* | Given a well-behaved vector function A, Gauss' theorem shows
that the same result will be obtained by integrating its divergence
over a volume V or by integrating its normal component over the
surface S that encloses that volume. The following steps exemplify
this fact. Consider the particular vector function A = (Ao/d)(x
ix + y iy) and a cubical volume having surfaces in the planes
x =  d, y = d, y =  d, and z = d, and z =  d. d.
|
| 2.2.2 | With A = (Ao/d3)(xy2 ix + x2 y iy), carry out the
steps in Prob. 2.2.1.
|
| | Continuity, and Charge Conservation
|
|---|
| 2.3.1* | For a line charge along the z axis of Prob. 1.3.1, E was
written in Cartesian coordinates as (a).
| (a) | Use Gauss' differential law in Cartesian coordinates to show that the charge density is indeed
zero everywhere except along the z axis.
|
| (b) | Obtain the same result by
evaluating Gauss' law using E as given by (1.3.13) and the
divergence operator from Table I in cylindrical coordinates.
|
|
| 2.3.2* | Show that at each point r < a, E and 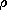 as given respectively
by (b) and (a) of Prob. 1.3.3 are consistent with Gauss'
differential law. as given respectively
by (b) and (a) of Prob. 1.3.3 are consistent with Gauss'
differential law.
|
| 2.3.3* | For the flux linkage 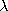 f to be independent of S, (2) must
hold. Return to Prob. 1.6.6 and check to see that this condition was
indeed satisfied by the magnetic flux density. f to be independent of S, (2) must
hold. Return to Prob. 1.6.6 and check to see that this condition was
indeed satisfied by the magnetic flux density.
|
| 2.3.4* | Using H expressed in cylindrical coordinates
by (1.4.10), show that the magnetic flux density of a line current
is indeed solenoidal (has no divergence) everywhere except at r = 0.
|
| 2.3.5 | Use the differential law of magnetic flux continuity, (2), to
answer Prob. 1.7.2.
|
| 2.3.6* | In Prob. 1.3.5, E and 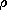 are found for a one-dimensional
configuration using the integral charge conservation law. Show that
the differential form of this law is satisfied at each position
- are found for a one-dimensional
configuration using the integral charge conservation law. Show that
the differential form of this law is satisfied at each position
- 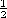 s < z < s < z < 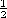 s. s.
|
| 2.3.7 | For J and 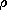 as found in Prob. 1.5.1, show that the
differential form of charge conservation, (3), is satisfied. as found in Prob. 1.5.1, show that the
differential form of charge conservation, (3), is satisfied.
|
| | The Curl Operator |
|---|
| 2.4.1* | Show that the curls of the three vector functions given in Prob.
2.1.2 are zero. Devise three such functions that have finite curls
(are rotational) and give their curls.
|
| 2.4.2 | Vector functions are given in cylindrical coordinates in Prob.
2.1.3. Using the curl operator as given in cylindrical coordinates by
Table I at the end of the text, show that all of these functions are
irrotational. Devise three functions that are rotational and give
their curls.
|
| 2.4.3* | In cylindrical coordinates, define incremental surface elements
having normals in the r,  and z directions, respectively, as
shown in Fig.~P2.4.3. Determine the r, and z directions, respectively, as
shown in Fig.~P2.4.3. Determine the r,  , and z components
of the curl operator. Show that the result is as given in Table I at
the end of the text. (Hint: In integrating in the , and z components
of the curl operator. Show that the result is as given in Table I at
the end of the text. (Hint: In integrating in the  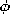 directions on the outer and inner incremental contours of
Fig.~P2.4.3c, note that not only is A
directions on the outer and inner incremental contours of
Fig.~P2.4.3c, note that not only is A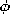 evaluated at r = r evaluated at r = r 
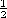  r, respectively, but so also is r. It is
therefore convenient to treat A r, respectively, but so also is r. It is
therefore convenient to treat A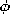 r as a single function.) r as a single function.)
|
| 2.4.4 | In spherical coordinates, incremental surface elements have normals
in the r, 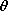 , and , and 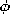 directions, respectively, as described in
Appendix 1. Determine the r, directions, respectively, as described in
Appendix 1. Determine the r, 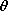 , and , and 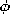 components of the
curl operator and compare to the result given in Table I at the end of
the text. components of the
curl operator and compare to the result given in Table I at the end of
the text.
|
| 2.4.5 | The following is an identity.
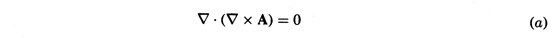 This can be shown in two ways.
This can be shown in two ways.
| (a) | Apply Stokes' theorem to an arbitrary but closed surface S (one having no edge, so C = 0) and
then Gauss' theorem to argue the identity.
|
| (b) | Write out the the divergence of the curl in Cartesian
coordinates and show that it is indeed identically zero.
|
|
| | Stokes' Integral Theorem |
|---|
| 2.5.1* | To exemplify Stokes' integral theorem, consider the evaluation of
(4) for the vector function A = (Ao /d2) x2 iy
and a rectangular contour consisting of the segments at x = g +
 , y = h, x = g, and y = 0. The direction of the
contour is such that da = iz dxdy. , y = h, x = g, and y = 0. The direction of the
contour is such that da = iz dxdy.
| (a) | Show that the left-hand side of (4) is h Ao [(g +  )2 - g2]d2. )2 - g2]d2.
|
| (b) | Verify (4) by obtaining the same
result integrating curl A over the area enclosed by C.
|
|
| 2.5.2 | For the vector function A = (Ao /d)(-ix y + iy x),
evaluate the contour and surface integrals of (4) on C and S as
prescribed in Prob. 2.5.1 and show that they are equal.
|
| | Differential Laws of Ampère and Faraday |
|---|
| 2.6.1* | In Prob. 1.4.2, H is given in Cartesian coordinates by (c).
With 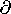  o E / o E /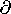 t = 0, show that Ampère's differential
law is satisfied at each point r < a. t = 0, show that Ampère's differential
law is satisfied at each point r < a.
|
| 2.6.2* | For the H and J given in Prob. 1.4.1, show that Ampère's
differential law, (2), is satisfied with 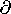  o E / o E /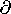 t = 0. t = 0.
|
| | Visualization of fields and the Divergence and Curl
|
|---|
| 2.7.1 | Using the conventions exemplified in Fig. 2.7.3,
| (a) | Sketch the distributions of charge density 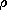 and
electric field intensity E for Prob. 1.3.5 and with Eo = 0 and and
electric field intensity E for Prob. 1.3.5 and with Eo = 0 and
 o = 0. o = 0.
|
| (b) | Verify that E is irrotational.
|
| (c) | From observation of the field sketch, why would you
suspect that E is indeed irrotational?
|
|
| 2.7.2 | Using Fig. 2.7.4 as a model, sketch J and H
| (a) | For Prob. 1.4.1.
|
| (b) | For Prob. 1.4.4.
|
| (c) | Verify that in each case, H is solenoidal.
|
| (d) | From observation of these field sketches, why would
you suspect that H is indeed solenoidal?
|
|
| 2.7.3 | Three two-dimensional vector fields are shown in Fig.~P2.7.3.
| (a) | Which of these is irrotational?
|
| (b) | Which are solenoidal?
|
|
| 2.7.4 | For the fields of Prob. 1.6.7, sketch E just above and just
below the plane y = 0 and  s in the surface y = 0.
Assume that E1 = E2 = s in the surface y = 0.
Assume that E1 = E2 =  o / o / o > 0 and adhere to the
convention that the field intensity is represented by the spacing of
the field lines. o > 0 and adhere to the
convention that the field intensity is represented by the spacing of
the field lines.
|
| 2.7.5 | For the fields of Prob. 1.7.3, sketch H just above and just
below the plane y = 0 and K in the surface y = 0. Assume that
H1 = H2 = Ko > 0 and represent the intensity of H by the
spacing of the field lines.
|
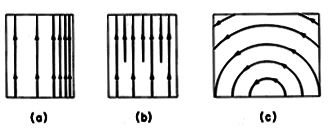
| 2.7.6 | Field lines in the vicinity of the surface y = 0 are shown in
Fig.~P2.7.6.
charge density  s on the surface. Is s on the surface. Is  s positive or
negative? s positive or
negative?
| (a) | If the field lines represent E, there is a surface
|
| (b) | If the field lines represent H, there is a surface
current density K = Kz iz on the surface. Is Kz
positive or negative?
|
|


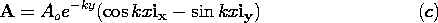
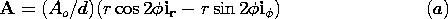
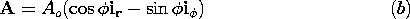

 r, r
r, r
 ,
,  z)
is as shown in Fig.~P2.1.4b. Determine the divergence operator by
evaluating (2), using steps analogous to those leading from (3)
to (5). Show that the result is as given in Table I at the end of
the text. (Hint: In carrying out the integrations over the surface
elements in Fig.~P2.1.4b having normals
z)
is as shown in Fig.~P2.1.4b. Determine the divergence operator by
evaluating (2), using steps analogous to those leading from (3)
to (5). Show that the result is as given in Table I at the end of
the text. (Hint: In carrying out the integrations over the surface
elements in Fig.~P2.1.4b having normals  ir, note that not
only is Ar evaluated at r = r
ir, note that not
only is Ar evaluated at r = r 
 r, but so also is
r. For this
reason, it is most convenient to group Ar and r together in
manipulating the contributions from this surface.)
r, but so also is
r. For this
reason, it is most convenient to group Ar and r together in
manipulating the contributions from this surface.)



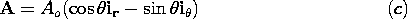
 r, r\Delta
r, r\Delta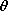 , r sin
, r sin 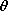 \Delta
\Delta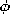 . Using
steps analogous to those
leading from (3) to (5), determine the divergence operator by evaluating
(2.1.2). Show that the result is as given in Table I at the end of
the text.
. Using
steps analogous to those
leading from (3) to (5), determine the divergence operator by evaluating
(2.1.2). Show that the result is as given in Table I at the end of
the text.
 d, y =
d, y =  d, and z =
d, and z =  d.
d.
 ix dydz,
ix dydz,  iy dxdz, and
iy dxdz, and  iz dydx.
iz dydx.
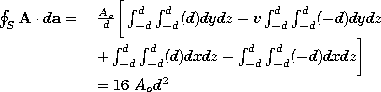
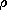 as given respectively
by (b) and (a) of Prob. 1.3.3 are consistent with Gauss'
differential law.
as given respectively
by (b) and (a) of Prob. 1.3.3 are consistent with Gauss'
differential law.
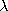 f to be independent of S, (2) must
hold. Return to Prob. 1.6.6 and check to see that this condition was
indeed satisfied by the magnetic flux density.
f to be independent of S, (2) must
hold. Return to Prob. 1.6.6 and check to see that this condition was
indeed satisfied by the magnetic flux density.
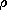 are found for a one-dimensional
configuration using the integral charge conservation law. Show that
the differential form of this law is satisfied at each position
-
are found for a one-dimensional
configuration using the integral charge conservation law. Show that
the differential form of this law is satisfied at each position
- 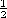 s < z <
s < z < 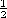 s.
s.
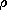 as found in Prob. 1.5.1, show that the
differential form of charge conservation, (3), is satisfied.
as found in Prob. 1.5.1, show that the
differential form of charge conservation, (3), is satisfied.

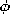 and z directions, respectively, as
shown in Fig.~P2.4.3. Determine the r,
and z directions, respectively, as
shown in Fig.~P2.4.3. Determine the r, 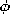 , and z components
of the curl operator. Show that the result is as given in Table I at
the end of the text. (Hint: In integrating in the
, and z components
of the curl operator. Show that the result is as given in Table I at
the end of the text. (Hint: In integrating in the 
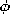 directions on the outer and inner incremental contours of
Fig.~P2.4.3c, note that not only is A
directions on the outer and inner incremental contours of
Fig.~P2.4.3c, note that not only is A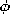 evaluated at r = r
evaluated at r = r 
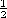
 r, respectively, but so also is r. It is
therefore convenient to treat A
r, respectively, but so also is r. It is
therefore convenient to treat A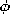 r as a single function.)
r as a single function.)
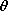 , and
, and 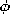 directions, respectively, as described in
Appendix 1. Determine the r,
directions, respectively, as described in
Appendix 1. Determine the r, 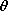 , and
, and 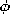 components of the
curl operator and compare to the result given in Table I at the end of
the text.
components of the
curl operator and compare to the result given in Table I at the end of
the text.
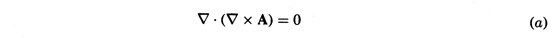
 , y = h, x = g, and y = 0. The direction of the
contour is such that da = iz dxdy.
, y = h, x = g, and y = 0. The direction of the
contour is such that da = iz dxdy.
 )2 - g2]d2.
)2 - g2]d2.
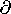
 o E /
o E /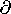 t = 0, show that Ampère's differential
law is satisfied at each point r < a.
t = 0, show that Ampère's differential
law is satisfied at each point r < a.
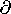
 o E /
o E /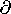 t = 0.
t = 0.
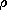 and
electric field intensity E for Prob. 1.3.5 and with Eo = 0 and
and
electric field intensity E for Prob. 1.3.5 and with Eo = 0 and
 o = 0.
o = 0.

 s in the surface y = 0.
Assume that E1 = E2 =
s in the surface y = 0.
Assume that E1 = E2 =  o /
o / o > 0 and adhere to the
convention that the field intensity is represented by the spacing of
the field lines.
o > 0 and adhere to the
convention that the field intensity is represented by the spacing of
the field lines.
 s on the surface. Is
s on the surface. Is  s positive or
negative?
s positive or
negative?


