In this chapter, the divergence and curl operators have been introduced. A third, the gradient, is naturally defined where it is put to use, in Chap. 4. A summary of these operators in the three standard coordinate systems is given in Table I at the end of the text. The problems for Secs. 2.1 and 2.4 outline the derivations of the gradient and curl operators in cylindrical and spherical coordinates.
The integral theorems of Gauss and Stokes are two of three theorems summarized in Table II at the end of the text. Gauss' theorem states how the volume integral of any scalar that can be represented as the divergence of a vector can be reduced to an integration of the normal component of that vector over the surface enclosing that volume. A volume integration is reduced to a surface integration. Similarly, Stokes' theorem reduces the surface integration of any vector that can be represented as the curl of another vector to a contour integration of that second vector. A surface integral is reduced to a contour integral.
These generally useful theorems are the basis for moving from the integral law point of view of Chap. 1 to a differential point of view. This transition from a global to a point-wise view of fields is summarized by the shift from the integral laws of Table 1.8.1 to the differential laws of Table 2.8.1.
The aspects of a vector field encapsulated in the divergence and curl can always be recalled by returning to the fundamental definitions, (2.1.2) and (2.4.2), respectively. The divergence is indeed defined to represent the net outward flux through a closed surface. But keep in mind that the surface is incremental, and that the divergence describes only the neighborhood of a given point. Similarly, the curl represents the circulation around an incremental contour, not around one that is of finite size.
What should be committed to memory from this chapter? The theorems of Gauss and Stokes are the key to relating the integral and differential forms of Maxwell's equations. Thus, with these theorems and the integral laws in mind, it is easy to remember the differential laws. Applied to differential volumes and surfaces, the theorems also provide the definitions (and hence the significances) of the divergence and curl operators independent of the coordinate system. Also, the evaluation in Cartesian coordinates of these operators should be remembered.
TABLE 2.8.1 MAXWELL'S DIFFERENTIAL LAWS IN FREE SPACE
Name Differential Law Eq. Number Gauss' Law 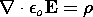2.3.1 Ampère's Law 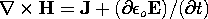2.6.2 Faraday's Law 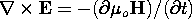2.6.4 Magnetic Flux Continuity 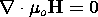2.3.2 Charge Conservation 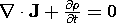2.3.3
