The laws represented by Maxwell's equations are remarkably general. Nevertheless, they are deceptively simple. In differential form they are
The sources of the electric and magnetic field intensities, E and H, are the charge and current densities,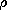
and J.
If, at an initial instant, electric and magnetic fields are specified throughout all of a source-free space, then Maxwell's equations in their differential form predict these fields as they subsequently evolve in space and time. Proof of this assertion is our starting point in Sec. 3.1. This makes it natural to attribute a physical significance to the fields in their own right. Fields can exist in regions far removed from their sources because they can propagate as electromagnetic waves. An introduction to such waves is given in Sec. 3.2. It is shown that the coupling between E and H produced by the magnetic induction in Faraday's law, the term on the right in (1) and the displacement current density in Ampère's law, the time derivative term on the right in (2), gives rise to electromagnetic waves.
Even though fields can propagate without sources, where they are initiated or detected they must be related to their sources or sinks. To do this, the Lorentz force law must be brought into play. In Sec. 3.1, this law is used to complete Newton's law and describe the evolution of a charge distribution. Generally, the Lorentz force law does not act so directly as it does in this example; nevertheless, it usually underlies a constitutive law for conduction that is added to Maxwell's equations to relate the fields to the sources. The most commonly used constitutive law is Ohm's law, which is not introduced until Chap. 7. However, in the intervening chapters we will often model electrodes and wires as being perfectly conducting in the sense that Lorentz's law is responsible for making the charges move in just such a way that there is effectively no electric field intensity in the material.
Maxwell's equations describe the most intricate electromagnetic wave phenomena. Of course, the analysis of such fields is difficult and not always necessary. Wave phenomena occur on short time scales or at high frequencies that are often of no practical concern. If this is the case, the fields may be described by truncated versions of Maxwell's equations applied to relatively long time scales and low frequencies (quasistatics). The objective in Sec. 3.3 is to identify the two quasistatic approximations and rank the laws in order of importance in these approximations.
In Sec. 3.4, we find what turns out to be one typical condition that must be satisfied if either of these quasistatic approximations is to be justified. Thus, we will find that a system composed of perfect conductors and free space is either electroquasistatic (EQS) or magnetoquasistatic (MQS) if an electromagnetic wave can propagate through a typical dimension of the system in a time that is shorter than times of interest.
If fulfillment of the same condition justifies either the EQS or MQS approximation, how do we know which to use? We begin to form insights in this regard in Sec. 3.4.
A formal justification of the quasistatic approximations would be based on what might be termed a time-rate expansion. As time rates of change are increased, more terms are required in a series having its first term predicted by the appropriate quasistatic laws. In Sec. 3.4, a specific example is used to illustrate this expansion and the error committed by omission of the higher-order terms.
Whether they be electromagnetic, or perhaps thermal or mechanical, dynamical systems that proceed from one state to another as though they are static are commonly said to be quasistatic in their behavior. In this text, the quasistatic fields are indeed related to their sources as if they were truly static. That is, given the charge or current distribution, E or H are determined without regard for the dynamics of electromagnetism. However, other dynamical processes can play a role in determining the source distributions.
In the systems we are prepared to consider in this chapter, composed of free space and perfect conductors, the quasistatic source distributions within a given quasistatic subregion do not depend on time rates of change. Thus, for now, we will find that geometry and spatial and temporal scales alone determine whether a subregion is magnetoquasistatic or electroquasistatic. Illustrated in Sec. 3.5 is the interconnection of such subsystems. In a way that is familiar from circuit theory, the resulting model for the total system has apportionments of sources in the subregions (charges in the EQS regions and currents in the MQS regions) that do depend on the time rates of change. After we have considered effects of finite conductivity in Chaps. 7 and 10, it will be clear that there are many other situations where quasistatic models represent dynamical processes.
Again, Sec. 3.6 provides an overview, this time not of the laws but rather of the parts of the physical world to which they pertain. The discussion is qualitative and the section is for "feet on the table" reading. Finally, Sec. 3.7 summarizes the electroquasistatic and magnetoquasistatic field laws that, respectively, are the themes of Chaps. 4-7 and 8-10.
We return to the subject of quasistatic approximations in Chap. 12, where electromagnetic waves are again considered. In Chap. 15 we will come to recognize that the concept of quasistatics promulgated in Chaps. 7 and 10 (where loss phenomena are considered) has made the classification into electroquasistatic and magnetoquasistatic regions depend not only on geometry and spatial and temporal scales, but on material properties as well.
