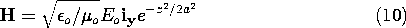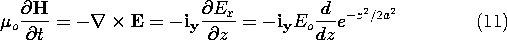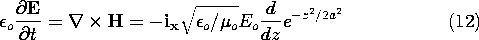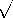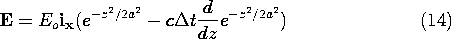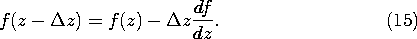If certain initial conditions are given, Maxwell's equations, along with the Lorentz law and Newton's law, describe the time evolution of E and H. This can be argued by expressing Maxwell's equations, (1)-(4), with the time derivatives and charge density on the left.




The region of interest is vacuum, where particles having a mass m and charge q are subject only to the Lorentz force. Thus, Newton's law (here used in its nonrelativistic form), also written with the time derivative (of the particle velocity) on the left, links the charge distribution to the fields.
The Lorentz force on the right is given by (1.1.1).
Suppose that at a particular instant, t = to, we are given the fields throughout the entire space of interest, E (r,to) and H(r,to). Suppose we are also given the velocity v(r, to) of all the charges when t = to. It follows from Gauss' law, (3), that at this same instant, the distribution of charge density is known.

Then the current density at the time t = to follows as

So that (4) is satisfied when t = to, we must require that the given distribution of H be solenoidal.
The curl operation involves only spatial derivatives, so the
right-hand sides of the remaining laws, (1), (2), and (5), can now be
evaluated. Thus, the time rates of change of the quantities,
E, H, and
v, given when t = to, are now known. This allows evaluation
of these quantities an instant later, when t = to + 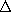 t. For
example, at this later time,
t. For
example, at this later time,

Thus, when t = to + 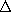 t we have the same
three vector functions throughout all space we started with. This
process can be repeated iteratively to determine the distributions at
an arbitrary later time. Note that if the initial distribution of
H is solenoidal, as required by (4), all subsequent
distributions will be solenoidal as well. This follows by taking the
divergence of Faraday's law, (1), and noting that the divergence of
the curl is zero.
t we have the same
three vector functions throughout all space we started with. This
process can be repeated iteratively to determine the distributions at
an arbitrary later time. Note that if the initial distribution of
H is solenoidal, as required by (4), all subsequent
distributions will be solenoidal as well. This follows by taking the
divergence of Faraday's law, (1), and noting that the divergence of
the curl is zero.
The left-hand side of (5) is written as a total derivative because it is required to represent the time derivative as measured by an observer moving with a given particle.
The preceding argument shows that in free space, for given initial E, H, and v, the Lorentz law (here used with Newton's law) and Maxwell's equations determine the charge distributions and the associated fields for all later time. In this sense, Maxwell's equations and the Lorentz law may be said to provide a complete description of electrodynamic interactions in free space. Commonly, more than one species of charge is involved and the charged particles respond to the field in a manner more complex than simply represented by the laws of Newton and Lorentz. In that case, the role played by (5) is taken by a conduction constitutive law which nevertheless reflects the Lorentz force law.
Another interesting property of Maxwell's equations emerges from the preceding discussion. The electric and magnetic fields are coupled. The temporal evolution of E is determined in part by the curl of H, (2), and, similarly, it is the curl of E that determines how fast H is changing in time, (1).
Example 3.1.1. Evolution of an Electromagnetic Wave
The interplay of the magnetic induction and the electric displacement current is illustrated by considering fields that evolve in Cartesian coordinates from the initial distributions
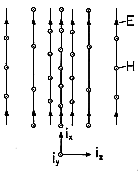
In this example, we let to = 0, so these are the fields when t = 0. Shown in Fig. 3.1.1, these fields are transverse, in that they have a direction perpendicular to the coordinate upon which they depend. Thus, they are both solenoidal, and Gauss' law makes it clear that the physical situation we consider does not involve a charge density. It follows from (7) that the current density is also zero.
Figure 3.1.1 A schematic representation of the E and H fields of Example 3.2.1. The distributions move to the right with the speed of light, c. With the initial fields given and J = 0, the right-hand sides of (1) and (2) can be evaluated to give the rates of change of H and E.
It follows from (11), Faraday's law, that when t =
t,
where c = 1/
o
o, and from (12), Ampère's law, that the electric field is
When t =
t, the E and H fields are equal to the original Gaussian distribution minus c
t times the spatial derivatives of these Gaussians. But these represent the original Gaussians shifted by c
t in the +z direction. Indeed, witness the relation applicable to any function f(z).
On the left, f(z -
z) is the function f(z) shifted by
z. The Taylor expansion on the right takes the same form as the fields when t =
t, (13) and (14). Thus, within
t, the E and H field distributions have shifted by c
t in the +z direction. Iteration of this process shows that the field distributions shown in Fig. 3.1.1 travel in the +z direction without change of shape at the speed c, the speed of light.
Note that the derivation would not have changed if we had substituted for the initial Gaussian functions any other continuous functions f(z).
In retrospect, it should be recognized that the initial conditions were premeditated so that they would result in a single wave propagating in the +z direction. Also, the method of solution was really not numerical. If we were interested in pursuing the numerical approach, care would have to be taken to avoid the accumulation of errors.
The above example illustrated that the electromagnetic wave is caused by the interplay of the magnetic induction and the displacement current, the terms on the left in (1) and (2). Through Faraday's law, (1), the curl of an initial E implies that an instant later, the initial H is altered. Similarly, Ampère's law requires that the curl of an initial H leads to a change in E. In turn, the curls of the altered E and H imply further changes in H and E, respectively.
There are two main points in this section. First, Maxwell's equations, augmented by laws describing the interaction of the fields with the sources, are sufficient to describe the evolution of electromagnetic fields.
Second, in regions well removed from materials, electromagnetic fields evolve as electromagnetic waves. Typically, the time required for fields to propagate from one region to another, say over a distance L, is

where c is the velocity of light. The origin of these waves is the coupling between the laws of Faraday and Ampère afforded by the magnetic induction and the displacement current. If either one or the other of these terms is neglected, so too is any electromagnetic wave effect.