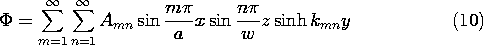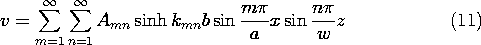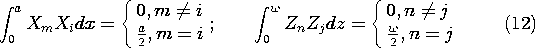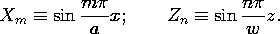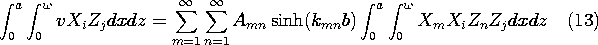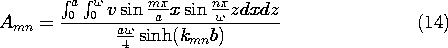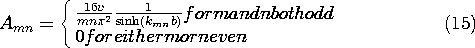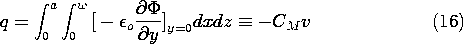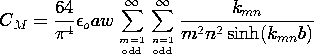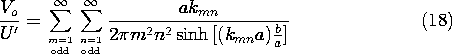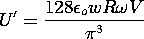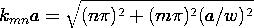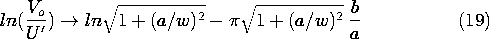Natural boundaries enclosing volumes in which Poisson's equation is to be satisfied are shown in Fig. 5.10.1 for the three standard coordinate systems. In general, the distribution of potential is desired within the volume with an arbitrary potential distribution on the bounding surfaces.
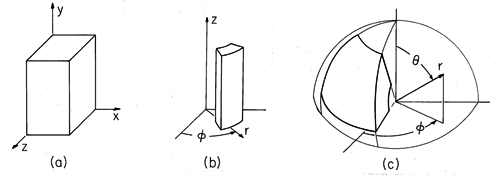
Considered first in this section is the extension of the Cartesian coordinate two-dimensional product solutions and modal expansions introduced in Secs. 5.4 and 5.5 to three dimensions. Given an arbitrary potential distribution over one of the six surfaces of the box shown in Fig. 5.10.1, and given that the other five surfaces are at zero potential, what is the solution to Laplace's equation within? If need be, a superposition of six such solutions can be used to satisfy arbitrary conditions on all six boundaries.
To use the same modal approach in configurations where the boundaries are natural to other than Cartesian coordinate systems, for example the cylindrical and spherical ones shown in Fig. 5.10.1, essentially the same extension of the basic ideas already illustrated is used. However, the product solutions involve less familiar functions. For those who understand the two-dimensional solutions, how they are used to meet arbitrary boundary conditions and how they are extended to three-dimensional Cartesian coordinate configurations, the literature cited in this section should provide ready access to what is needed to exploit solutions in new coordinate systems. In addition to the three standard coordinate systems, there are many others in which Laplace's equation admits product solutions. The latter part of this section is intended as an introduction to these coordinate systems and associated product solutions.
Cartesian Coordinate Product Solutions
In three-dimensions, Laplace's equation is
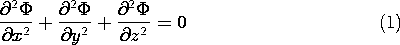
We look for solutions that are expressible as products of a function of x alone, X(x), a function of y alone, Y(y), and a function of z alone, Z(z).

Introducing (2) into (1) and dividing by  , we obtain
, we obtain
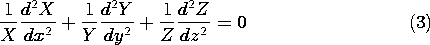
A function of x alone, added to one of y alone and one of of z alone, gives zero. Because x, y, and z are independent variables, the zero sum is possible only if each of these three "functions" is in fact equal to a constant. The sum of these constants must then be zero.
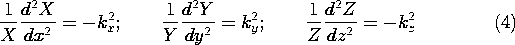

Note that if two of these three separation constants are positive, it is then necessary that the third be negative. We anticipated this by writing (4) accordingly. The solutions of (4) are
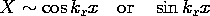
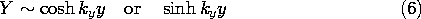

where
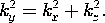
Of course, the roles of the coordinates can be interchanged, so either the x or z directions could be taken as having the exponential dependence. From these solutions it is evident that the potential cannot be periodic or be exponential in its dependencies on all three coordinates and still be a solution to Laplace's equation. In writing (6) we have anticipated satisfying potential constraints on planes of constant y by taking X and Z as periodic.
Modal Expansion in Cartesian Coordinates
It is possible to choose the constants and the solutions from (6) so that zero potential boundary conditions are met on five of the six boundaries. With coordinates as shown in Fig. 5.10.1a, the sine functions are used for X and Z to insure a zero potential in the planes x = 0 and z = 0. To make the potential zero in planes x = a and z = w, it is necessary that
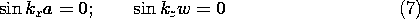
Solution of these eigenvalue equations gives kx = m /a, kz =
n
/a, kz =
n /w, and hence
/w, and hence
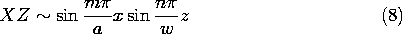
where m and n are integers.
To make the potential zero on the fifth boundary, say where y = 0, the hyperbolic sine function is used to represent the y dependence. Thus, a set of solutions, each meeting a zero potential condition on five boundaries, is
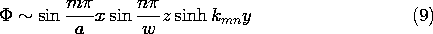
where in view of (5)
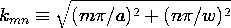
These can be used to satisfy an arbitrary potential constraint on the "last" boundary, where y = b. The following example, which extends Sec. 5.5, illustrates this concept.
Example 5.10.1. Capacitive Attenuator in Three Dimensions
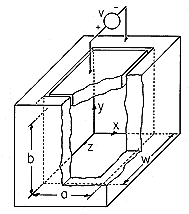
In the attenuator of Example 5.5.1, the two-dimensional field distribution is a good approximation because one cross-sectional dimension is small compared to the other. In Fig. 5.5.5, a \ll w. If the cross-sectional dimensions a and w are comparable, as shown in Fig. 5.10.2, the field can be represented by the modal superposition given by (9).
Figure 5.10.2 Region bounded by zero potentials at x = 0, x = a, z = 0, z = w, and y = 0. Electrode constrains plane y = b to have potential v. In the five planes x = 0, x = a, y = 0, z = 0, and z = w the potential is zero. In the plane y = b, it is constrained to be v by an electrode connected to a voltage source.
Evaluation of (10) at the electrode surface must give v.
The coefficients Amn are determined by exploiting the orthogonality of the eigenfunctions. That is,
where
The steps that now lead to an expression for any given coefficient Amn are a natural extension of those used in Sec. 5.5. Both sides of (11) are multiplied by the eigenfunction Xi Zj and then both sides are integrated over the surface at y = b.
Because of the product form of each term, the integrations can be carried out on x and z separately. In view of the orthogonality conditions, (12), the only none-zero term on the right comes in the summation with m = i and n = j. This makes it possible to solve the equation for the coefficient Aij. Then, by replacing i
m and j \rightarrow n, we obtain
The integral can be carried out for any given distribution of potential. In this particular situation, the potential of the surface at y = b is uniform. Thus, integration gives
The desired potential, satisfying the boundary conditions on all six surfaces, is given by (10) and (15). Note that the first term in the solution we have found is not the same as the first term in the two-dimensional field representation, (5.5.9). No matter what the ratio of a to w, the first term in the three-dimensional solution has a sinusoidal dependence on z, while the two-dimensional one has no dependence on z.
For the capacitive attenuator of Fig. 5.5.5, what output signal is predicted by this three dimensional representation? From (10) and (15), the charge on the output electrode is
where
With v = V sin
t, we find that vo = Vo cos
t where
Using (16), it follows that the amplitude of the output voltage is
where the voltage is normalized to
and
This expression can be used to replace the plot of Fig. 5.5.5. Here we compare the two-dimensional and three-dimensional predictions of output voltage by considering (18) in the limit where b
a. In this limit, the hyperbolic sine is dominated by one of its exponentials, and the first term in the series gives
In the limit a/w \ll 1, the dependence on spacing between input and output electrodes expressed by the right hand side becomes identical to that for the two-dimensional model, (5.5.15). However, U' = (8/
2 )U regardless of a/w.
This three-dimensional Cartesian coordinate example illustrates how the orthogonality property of the product solution is exploited to provide a potential that is zero on five of the boundaries while assuming any desired distribution on the sixth boundary. On this sixth surface, the potential takes the form

where
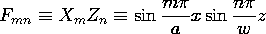
The two-dimensional functions Fmn have been used to represent the "last" boundary condition. This two-dimensional Fourier series replaces the one-dimensional Fourier series of Sec. 5.5 (5.5.17). In the example, it represents the two-dimensional square wave function shown in Fig. 5.10.3. Note that this function goes to zero along x = 0, x = a and z = 0, z = w, as it should. It changes sign as it passes through any one of these "nodal" lines, but the range outside the original rectangle is of no physical interest, and hence the behavior outside that range does not affect the validity of the solution applied to the example. Because the function represented is odd in both x and y, it can be represented by sine functions only.
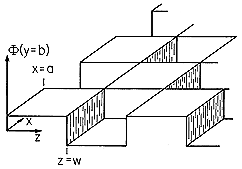
Our foray into three-dimensional modal expansions extends the notion of orthogonality of functions with respect to a one-dimensional interval to orthogonality of functions with respect to a two-dimensional section of a plane. We are able to determine the coefficients Vmn in (20) as it is made to fit the potential prescribed on the "sixth" surface because the terms in the series are orthogonal in the sense that
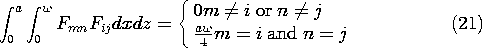
In other coordinate systems, a similar orthogonality relation will hold for the product solutions evaluated on one of the surfaces defined by a constant natural coordinate. In general, a weighting function multiplies the eigenfunctions in the integrand of the surface integral that is analogous to (21).
Except for some special cases, this is as far as we will go in considering three-dimensional product solutions to Laplace's equation. In the remainder of this section, references to the literature are given for solutions in cylindrical, spherical, and other coordinate systems.
Modal Expansion in Other Coordinates
A general volume having natural boundaries in cylindrical coordinates is shown in Fig. 5.10.1b. Product solutions to Laplace's equation take the form

The polar coordinates of Sec. 5.7 are a special case where Z(z) is a constant.
The ordinary differential equations, analogous to (4) and (5),
that determine F( ) and Z(z), have constant coefficients,
and hence the
solutions are sines and cosines of m
) and Z(z), have constant coefficients,
and hence the
solutions are sines and cosines of m and kz, respectively.
The radial
dependence is predicted by an ordinary differential equation that,
like (5.7.5), has space-varying coefficients. Unfortunately, with
the z dependence, solutions are not simply polynomials. Rather, they
are Bessel's functions of order m and argument kr. As applied to
product solutions to Laplace's equation, these functions
are described in standard fields texts[1-4]. Bessel's and
associated functions are developed in mathematics texts and
treatises[5-8].
and kz, respectively.
The radial
dependence is predicted by an ordinary differential equation that,
like (5.7.5), has space-varying coefficients. Unfortunately, with
the z dependence, solutions are not simply polynomials. Rather, they
are Bessel's functions of order m and argument kr. As applied to
product solutions to Laplace's equation, these functions
are described in standard fields texts[1-4]. Bessel's and
associated functions are developed in mathematics texts and
treatises[5-8].
As has been illustrated in two- and now three-dimensions, the
solution to an arbitrary potential distribution on the boundaries can
be written as the superposition of solutions each having the desired
potential on one boundary and zero potential on the others. Summarized
in Table 5.10.1 are the forms taken by the product solution, (22),
in representing the potential for an arbitrary distribution on the
specified surface. For example, if the potential is imposed on a
surface of constant r, the radial dependence is given by Bessel's
functions of real order and imaginary argument. What is needed to
represent  in the constant r surface are functions that are periodic
in
in the constant r surface are functions that are periodic
in  and z, so we expect that these Bessel's functions have an
exponential-like dependence on r.
and z, so we expect that these Bessel's functions have an
exponential-like dependence on r.
| Surface of Constant |
R(r) | F( ) ) |
Z(z) |
| r | Bessel's functions of real order and imaginary argument (modified Bessel's functions) | trigonometric functions of real argument | trigonometric functions of real argument |
 |
Bessel's functions of imaginary order and imaginary argument | trigonometric functions of imaginary argument | trigonometric functions of real argument |
| z | Bessel's functions of real order and real argument | trigonometric functions of real argument | trigonometric functions of imaginary argument |
In spherical coordinates, product solutions take the form

From the cylindrical coordinate solutions, it might be guessed that
new functions are required to describe R(r). In fact, these turn
out to be simple polynomials. The  dependence is predicted by a
constant coefficient equation, and hence represented by familiar
trigonometric functions. But the
dependence is predicted by a
constant coefficient equation, and hence represented by familiar
trigonometric functions. But the 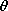 dependence is described by
Legendre functions. By contrast with the Bessel's functions, which
are described by infinite polynomial series, the Legendre functions
are finite polynomials in cos (
dependence is described by
Legendre functions. By contrast with the Bessel's functions, which
are described by infinite polynomial series, the Legendre functions
are finite polynomials in cos (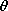 ). In connection with
Laplace's equation, the solutions are summarized in fields
texts[1-4]. As solutions to ordinary differential
equations, the Legendre polynomials are presented in mathematics
texts[5,7].
). In connection with
Laplace's equation, the solutions are summarized in fields
texts[1-4]. As solutions to ordinary differential
equations, the Legendre polynomials are presented in mathematics
texts[5,7].
The names of other coordinate systems suggest the surfaces generated by setting one of the variables equal to a constant: Elliptic-cylinder coordinates and prolate spheroidal coordinates are examples in which Laplace's equation is separable[2]. The first step in exploiting these new systems is to write the Laplacian and other differential operators in terms of those coordinates. This is also described in the given references.