The following development is applicable to polarization phenomena having diverse microscopic origins. Whether representative of atoms, molecules, groups of ordered atoms or molecules (domains), or even macroscopic particles, the dipoles are pictured as opposite charges
q separated by a vector distance d directed from the negative to the positive charge. Thus, the individual dipoles, represented as in Sec. 4.4, have moments p defined as
Because d is generally smaller in magnitude than the size of the atom, molecule, or other particle, it is small compared with any macroscopic dimension of interest.
Now consider a medium consisting of N such polarized particles per unit volume. What is the net charge q contained within an arbitrary volume V enclosed by a surface S? Clearly, if the particles of the medium within V were unpolarized, the net charge in V would be zero. However, now that they are polarized, some charge centers that were contained in V in their unpolarized state have moved out of the surface S and left behind unneutralized centers of charge. To determine the net unneutralized charge left behind in V, we will assume (without loss of generality) that the negative centers of charge are stationary and that only the positive centers of charge are mobile during the polarization process.
Consider the particles in the neighborhood of an element of area d a on the surface S, as shown in Fig. 6.1.1. All positive centers of charge now outside S within the volume dV = d
d a have left behind negative charge centers. These contribute a net negative charge to V. Because there are Nd
Figure 6.1.1 Volume element containing positive charges which have left negative charges on the other side of surface S.
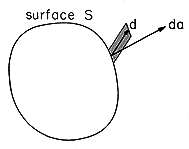
Note that the integrand can be either positive or negative depending on whether positive centers of charge are leaving or entering V through the surface element da. Which of these possibilities occurs is reflected by the relative orientation of d and da. If d has a component parallel (anti-parallel) to da, then positive centers of charge are leaving (entering) V through da.
The integrand of (1) has the dimensions of dipole moment per unit volume and will therefore be defined as the polarization density.
Also by definition, the net charge in V can be determined by integrating the polarization charge density over its volume.
Thus, we have two ways of calculating the net charge, the first by using the polarization density from (3) in the surface integral of (2).
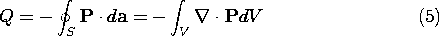
Here Gauss' theorem has been used to convert the surface integral to one over the enclosed volume. The charge found from this volume integral must be the same as given by the second way of calculating the net charge, by (4). Because the volume under consideration is arbitrary, the integrands of the volume integrals in (4) and (5) must be identical.
In this way, the polarization charge density
p has been related to the polarization density P.
It may seem that little has been accomplished in this development because, instead of the unknown
In Fig. 6.0.1, the polarized sphere could acquire no net charge. Our representation of the polarization charge density in terms of the polarization density guarantees that this is true. To see this, suppose V is interpreted as the volume containing the entire polarized body so that the surface S enclosing the volume V falls outside the body. Because P vanishes on S, the surface integral in (5) must vanish. Any distribution of charge density related to the polarization density by (6) cannot contribute a net charge to an isolated body.
We will often find it necessary to represent the polarization density by a discontinuous function. For example, in a material surrounded by free space, such as the sphere in Fig. 6.0.1, the polarization density can fall from a finite value to zero at the interface. In such regions, there can be a surface polarization charge density. With the objective of determining this density from P, (6) can be integrated over a pillbox enclosing an incremental area of an interface. With the substitution -P
o E and
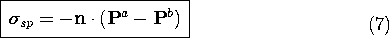
Just as (6) tells us how to determine the polarization charge density for a given distribution of P in the volume of a material, this expression serves to evaluate the singularity in polarization charge density (the surface polarization charge density) at an interface.
Note that according to (6), P originates on negative polarization charge and terminates on positive charge. This contrasts with the relationship between E and the charge density. For example, according to (6) and (7), the uniformly polarized cylinder of material shown in Fig. 6.1.2 with P pointing upward has positive
sp on the top and negative on the bottom.
Figure 6.1.2 Polarization surface charge due to uniform polarization of right cylinder.
