6.5
Fields in the Presence of Electrically LinearDielectrics

In Secs. 6.2 and 6.3, the polarization density was given independently of the electric field intensity. In this and the next two sections, the polarization is induced by the electric field. Not only does the electric field give rise to the polarization, but in return, the polarization modifies the field. The polarization feeds back on the electric field intensity.

This "feedback" is described by the constitutive law for a linear dielectric. Thus, (6.4.3) and Gauss' law, (6.2.15), combine to give

and the electroquasistatic form of Faraday's law requires that

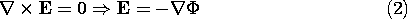
The continuity conditions implied by these two laws across an interface separating media having different permittivities are (6.2.16) expressed in terms of the constitutive law and either (5.3.1) or (5.3.4). These are

Figure 6.5.1 Field region filled by (a) uniform dielectric, (b) piece-wise uniform dielectric and (c) smoothly varying dielectric.

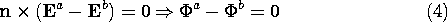
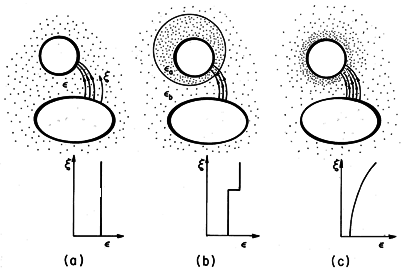
Figure 6.5.1 illustrates three classes of situations involving linear dielectrics. In the first, the entire region of interest is filled with a uniform dielectric. In the second, the region of interest can be broken into uniform subregions within which the permittivity is constant. The continuity conditions are needed to insure that the basic laws are satisfied through the interfaces between these regions. Systems of this type are said to be composed of piece-wise uniform dielectrics. Finally, the dielectric material may vary in its permittivity over dimensions that are on the same order as those of interest. Such a smoothly inhomogeneous dielectric is illustrated in Fig. 6.5.1c.

The remainder of this section makes some observations that are generally applicable provided that _u = 0 throughout the volume of the region of interest. Section 6.6 is devoted to systems having uniform and piece-wise uniform dielectrics, while Sec. 6.7 illustrates fields in smoothly inhomogeneous dielectrics.

Capacitance

How does the presence of a dielectric alter the capacitance? To answer this question, recognize that conservation of unpaired charge, as expressed by (6.2.13), still requires that the current i measured at terminals connected to a pair of electrodes is the time rate of change of the unpaired charge on the electrode. In view of Gauss' law, with the effects of polarization included, (6.2.15), the net unpaired charge on an electrode enclosed by a surface S is

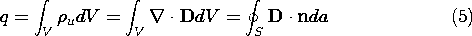
Here, Gauss' theorem has been used to convert the volume integral to a surface integral.

We conclude that the capacitance of an electrode (a) relative to a reference electrode (b) is

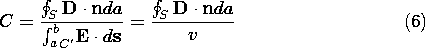
Note that this is the same as for electrodes in free space except that _o E D. Because there is no unpaired charge density in the region between the electrodes, S is any surface that encloses the electrode (a). As before, with no polarization, E is irrotational, and therefore C' is any contour connecting the electrode (a) to the reference (b).

In an electrically linear dielectric, where D = E, both the numerator and denominator of (6) are proportional to the voltage, and as a result, the capacitance C is independent of the voltage. However, with the introduction of an electrically nonlinear material, perhaps having the polarization constitutive law of Fig. 6.4.1, the numerator of (6) is not a linear function of the voltage. As defined by (6), the capacitance is then a function of the applied voltage.

Induced Polarization Charge

Stated as (1)-(4), the laws and continuity conditions for fields in a linear dielectric put the polarization charge out of view. Yet it is this charge that contains the effect of the dielectric on the field. Where does the polarization charge accumulate?

Again, assuming that _u is zero, a vector identity casts Gauss' law as given by (1) into the form

Multiplied by _o and divided by , this expression can be written as

Comparison of this expression to Gauss' law written in terms of _p, (6.2.1), shows that the polarization charge density is

This equation makes it clear that polarization charge will be induced only where there are gradients in . A special case is where there is an abrupt discontinuity in . Then the gradient in (9) is singular and represents a polarization surface charge density (the gradient represents the spatial derivative of a step function, which is an impulse). This surface charge density can best be determined by making use of the polarization charge density continuity condition, (6.1.7). Substitution of the constitutive law P = ( - _o)E then gives

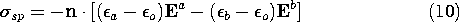
Because _su = 0, it follows from the jump condition for n D, (3), that

Remember that n is directed from region (b) to region (a).

Because D is solenoidal, we can construct tubes of D containing constant flux. Lines of D must therefore begin and terminate on the boundaries. The constitutive law, D = E, requires that D is proportional to E. Thus, although E can intensify or rarify as it passes through a flux tube, it can not reverse direction. Therefore, if we follow a bundle of electric field lines from the boundary point of high potential to the one of low potential, the polarization charge encountered [in accordance with (9) and (11)] is positive at points where is decreasing, negative where it is increasing.

Consider the examples in Fig. 6.5.1. In the case of the uniform dielectric, Fig. 6.5.1a, the typical flux tube shown passes through no variations in , and it follows from (8) that there is no volume polarization charge density. Thus, it will come as no surprise that the field distribution in this case is predicted by Laplace's equation.

In the piece-wise uniform dielectrics, there is no polarization charge density in a flux tube except where it passes through an interface. For the flux tube shown, (11) shows that if the upper region has the greater permittivity (_a > _b), then there is an accumulation of negative surface charge density at the interface. Thus, the field originating on positive charges at the lower electrode is in part terminated by negative polarization surface charge at the interface, and the field in the upper region tends to be weakened relative to that below.

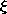In the smoothly inhomogeneous dielectric of Fig. 6.5.1c, the typical flux tube shown passes through a region where increases with . It follows from (8) that negative polarization charge density is induced in the volume of the material. Here again, the electric field associated with positive charge on the lower electrode is in part terminated on the polarization charge density induced in the volume. As a result, the dielectric tends to make the electric field weaken with increasing .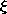

The next two sections give the opportunity to solve for the fields in simple configurations and then see that the results are consistent with the physical picture that has been found here.