Reading 4: Testing
Java Tutor exercises
Keep making progress on Java by completing the next three categories in the Java Tutor:
Software in 6.031
Objectives
After today’s class, you should:
- understand the value of testing, and know the process of test-first programming;
- be able to judge a test suite for correctness, thoroughness, and size;
- be able to design a test suite for a method by partitioning its input space and choosing good test cases;
- be able to judge a test suite by measuring its code coverage; and
- understand and know when to use black box vs. glass box testing, unit tests vs. integration tests, and automated regression testing.
Validation
Testing is an example of a more general process called validation. The purpose of validation is to uncover problems in a program and thereby increase your confidence in the program’s correctness. Validation includes:
- Formal reasoning about a program, usually called verification. Verification constructs a formal proof that a program is correct. Verification is tedious to do by hand, and automated tool support for verification is still an active area of research. Nevertheless, small, crucial pieces of a program may be formally verified, such as the scheduler in an operating system, or the bytecode interpreter in a virtual machine, or the filesystem in an operating system.
- Code review. Having somebody else carefully read your code, and reason informally about it, can be a good way to uncover bugs. It’s much like having somebody else proofread an essay you have written. We discuss code review in another reading.
- Testing. Running the program on carefully selected inputs and checking the results.
Even with the best validation, it’s very hard to achieve perfect quality in software. Here are some typical residual defect rates (bugs left over after the software has shipped) per kloc (one thousand lines of source code):
- 1 - 10 defects/kloc: Typical industry software.
- 0.1 - 1 defects/kloc: High-quality validation. The Java libraries might achieve this level of correctness.
- 0.01 - 0.1 defects/kloc: The very best, safety-critical validation. NASA and companies like Praxis can achieve this level.
This can be discouraging for large systems. For example, if you have shipped a million lines of typical industry source code (1 defect/kloc), it means you missed 1000 bugs!
Why software testing is hard
Here are some approaches that unfortunately don’t work well in the world of software.
Exhaustive testing is infeasible. The space of possible test cases is generally too big to cover exhaustively. Imagine exhaustively testing a 32-bit floating-point multiply operation, a*b. There are 264 test cases!
Haphazard testing (“just try it and see if it works”) is less likely to find bugs, unless the program is so buggy that an arbitrarily-chosen input is more likely to fail than to succeed. It also doesn’t increase our confidence in program correctness.
Random or statistical testing doesn’t work well for software. Other engineering disciplines can test small random samples (e.g. 1% of hard drives manufactured) and infer the defect rate for the whole production lot. Physical systems can use many tricks to speed up time, like opening a refrigerator 1000 times in 24 hours instead of 10 years. These tricks give known failure rates (e.g. mean lifetime of a hard drive), but they assume continuity or uniformity across the space of defects. This is true for physical artifacts.
But it’s not true for software. Software behavior varies discontinuously and discretely across the space of possible inputs. The system may seem to work fine across a broad range of inputs, and then abruptly fail at a single boundary point. The famous Pentium division bug affected approximately 1 in 9 billion divisions. Stack overflows, out of memory errors, and numeric overflow bugs tend to happen abruptly, and always in the same way, not with probabilistic variation. That’s different from physical systems, where there is often visible evidence that the system is approaching a failure point (cracks in a bridge) or failures are distributed probabilistically near the failure point (so that statistical testing will observe some failures even before the point is reached).
Instead, test cases must be chosen carefully and systematically. Techniques for systematic testing are the primary focus of this reading.
reading exercises
/**
* @param bits an array of 32 true/false values
* @return the Boolean AND of all values in the array
*/
boolean andAll(boolean[] bits) {
boolean result = bits[0];
for (int i = 1; i < 31; i++) {
result = result && bits[i];
}
return result;
}Louis Reasoner, who wrote this method and thinks it should work, tries it on a couple of haphazardly-chosen test cases shown below. What is the result of each test case?
andAll([true, true, true, ..., true, true]) // 32 true values
andAll([false, true, false, true, ..., false, true]) // 32 values alternating between false and true
Louis is satisfied. But unfortunately his code has an off-by-one error. Which expression has the bug?
(missing explanation)
Which is closest to the number of test cases required to test this function exhaustively?
(missing explanation)
Which is closest to the probability of finding the off-by-one bug with a random test (i.e. picking a single input to try, uniformly at random from the possible inputs)?
(missing explanation)
In the 1990s, the Ariane 5 launch vehicle, designed and built for the European Space Agency, self-destructed 37 seconds after its first launch.
The reason was a control software bug that went undetected. The Ariane 5’s guidance software was reused from the Ariane 4, which was a slower rocket. When the velocity calculation converted from a 64-bit floating point number (a double in Java terminology, though this software wasn’t written in Java) to a 16-bit signed integer (a short), it overflowed the small integer and caused an exception to be thrown. The exception handler had been disabled for efficiency reasons, so the guidance software crashed. Without guidance, the rocket crashed too. The cost of the failure was $1 billion.
What ideas does this story demonstrate?
(missing explanation)
Test-first programming
Before we dive in, we need to define some terms:
A module is a part of a software system that can be designed, implemented, tested, and reasoned about separately from the rest of the system. In this reading, we’ll focus on modules that are functions, represented by Java methods. In future readings we’ll broaden our view to think about larger modules, like a class with multiple interacting methods.
A specification (or spec) describes the behavior of a module. For a function, the specification gives the types of the parameters and any additional constraints on them (e.g.
sqrt’s parameter must be nonnegative). It also gives the type of the return value and how the return value relates to the inputs. In Java code, the specification consists of the method signature and the comment above it that describes what it does.A module has an implementation that provides its behavior, and clients that use the module. For a function, the implementation is the body of the method, and the clients are other code that calls the method. The specification of the module constrains both the client and the implementation. We’ll have much more to say about specifications, implementations, and clients a few classes from now.
A test case is a particular choice of inputs, along with the expected output behavior required by the specification.
You’ve already seen and used these concepts on problem set 0. You were given some specifications for Java methods and asked to write an implementation for each one. You were also given a test suite for each method that you could run to see if your implementation obeyed the spec.
It turns out that this is a good pattern to follow when designing a program from scratch. In test-first programming, you write the spec and the tests before you even write any code. The development of a single function proceeds in this order:
- Spec: Write a specification for the function.
- Test: Write tests that exercise the specification.
- Implement: Write the implementation.
Once your implementation passes the tests you wrote, you’re done.
The biggest benefit of test-first programming is safety from bugs. Don’t leave testing until the end of development, when you have a big pile of unvalidated code. Leaving testing until the end only makes debugging longer and more painful, because bugs may be anywhere in your code. It’s far more pleasant to test your code as you develop it.
reading exercises
Systematic testing
Rather than exhaustive, haphazard, or randomized testing, we want to test systematically. Systematic testing means that we are choosing test cases in a principled way, with the goal of designing a test suite with three desirable properties:
Correct. A correct test suite is a legal client of the specification, and it accepts all legal implementations of the spec without complaint. This gives us the freedom to change how the module is implemented internally without necessarily having to change the test suite.
Thorough. A thorough test suite finds actual bugs in the implementation, caused by mistakes that programmers are likely to make.
Small. A small test suite, with few test cases, is faster to write in the first place, and easier to update if the specification evolves. Small test suites are also faster to run. You will be able to run your tests more frequently if your test suites are small and fast.
By these criteria, exhaustive testing is thorough but infeasibly large. Haphazard testing tends to be small but not thorough. Randomized testing can achieve thoroughness only at the cost of large size.
Designing a test suite for both thoroughness and small size requires having the right attitude. Normally when you’re coding, your goal is to make the program work. But as a test suite designer, you want to make it fail. That’s a subtle but important difference. A good tester intentionally pokes at all the places the program might be vulnerable, so that those vulnerabilities can be eliminated.
The need to adopt a testing attitude is another argument for test-first programming. It is all too tempting to treat code you’ve already written as a precious thing, a fragile eggshell, and test it very lightly just to see it work. For thorough testing, though, you have to be brutal. Test-first programming allows you to put on your testing hat, and adopt that brutal perspective, before you’ve even written any code.
reading exercises
Choosing test cases by partitioning
Creating a good test suite is a challenging and interesting design problem. We want to pick a set of test cases that is small enough to be easy to write and maintain and quick to run, yet thorough enough to find bugs in the program.
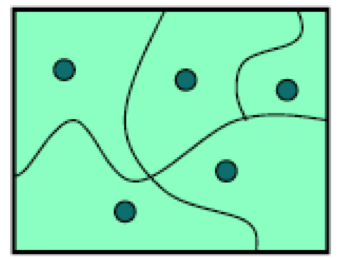
To do this, we divide the input space into subdomains, each consisting of a set of inputs. (The name subdomain comes from the fact that it is a subset of the domain, the input space of a mathematical function.) Taken together, the subdomains form a partition: a collection of disjoint sets that completely covers the input space, so that every input lies in exactly one subdomain. Then we choose one test case from each subdomain, and that’s our test suite.
The idea behind subdomains is to divide the input space into sets of similar inputs on which the program has similar behavior. Then we use one representative of each set. This approach makes the best use of limited testing resources by choosing dissimilar test cases, and forcing the testing to explore areas of the input space that random testing might not reach.
Example: abs()
Let’s start with a simple example from the Java library: the integer abs() function, found in the Math class:
/**
* ...
* @param a the argument whose absolute value is to be determined
* @return the absolute value of the argument.
*/
public static int abs(int a)(This is not the complete specification of abs, so we’ll come back to this later.
But it will do for a start.)
Mathematically, this method is a function of the following type:
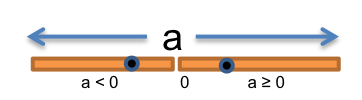
The function has a one-dimensional input space, consisting of all the possible values of a.
Thinking about how the absolute value function behaves, we might start by partitioning the input space into these two subdomains: { a | a ≥ 0 } and { a | a < 0 }.
On the first subdomain, abs should return a unchanged.
On the second subdomain, abs should negate it.
To write a partition compactly, we omit the { a | … } frame of each set description, and simply write a list of predicates like so:
// partition: a >= 0; a < 0To choose test cases for our test suite, we pick an arbitrary value a from each subdomain of the partition, for example:
Example: max()
Now let’s look at another example from the Java library: the integer max() function, also found in Math.
/**
* ...
* @param a an argument
* @param b another argument
* @return the larger of a and b.
*/
public static int max(int a, int b)Mathematically, this method is a function of two arguments:
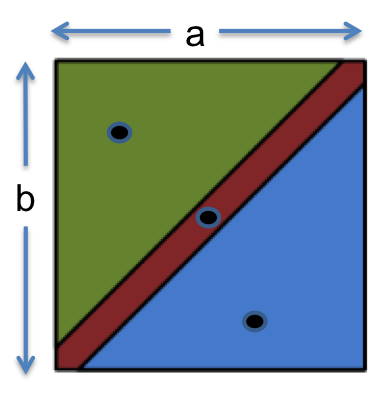
So we have a two-dimensional input space, consisting of all the pairs of integers (a,b). Now let’s partition it. From the specification, it makes sense to choose the subdomains { (a,b) | a < b } and { (a,b) | a > b }, because the spec calls for different behavior on each one. But we can’t stop there, because these subdomains are not yet a partition of the input space. A partition must completely cover the set of possible inputs. So we need to add { (a,b) | a = b }. Expressed compactly, the partition looks like this:
// partition: a < b; a > b; a = bOur test suite might then be:
reading exercises
Suppose you want to partition the input space of this integer square root function:
/**
* @param x must be nonnegative
* @returns nearest int to the square root of x
*/
public static int sqrt(int x)Assess the quality of each of the following candidate partitions. Are the proposed subdomains disjoint and complete, thus forming a partition? Are they correct, in the sense that each subdomain can be covered by a legal test case? A good partition should check all three boxes.
// partition: x < 0; x >= 0(missing explanation)
// partition: x is a perfect square; x is an integer > 0 but not a perfect square(missing explanation)
// partition: x=0, x=1, x=7, x=16(missing explanation)
Now consider this specification:
/**
* @param x an integer
* @param y an integer, where x and y are not both 0
* @return the greatest common divisor of x and y
*/
public static int gcd(int x, int y);Assess each of the following candidate partitions for gcd.
// partition: x and y are not both 0(missing explanation)
// partition: x is divisible by y; y is divisible by x; x and y are relatively prime(missing explanation)
Include boundaries in the partition
Bugs often occur at boundaries between subdomains. Some examples:
- 0 is a boundary between positive numbers and negative numbers
- the maximum and minimum values of numeric types, like
intordouble - emptiness for collection types, like the empty string, empty list, or empty set
- the first and last element of a sequence, like a string or list
Why do bugs often happen at boundaries?
One reason is that programmers often make off-by-one mistakes, like writing <= instead of <, or initializing a counter to 0 instead of 1.
Another is that some boundaries may need to be handled as special cases in the code.
Another is that boundaries may be places of discontinuity in the code’s behavior.
When an int variable grows beyond its maximum positive value, for example, it abruptly becomes a negative number.
It turns out that the abs function in Java behaves in a very unexpected way on one of these boundaries, which the spec describes as follows:
/**
* ...
* Note that if the argument is equal to the value of Integer.MIN_VALUE,
* the most negative representable int value, the result is that same value,
* which is negative.
* ...
*/So it’s possible for abs to return a negative integer!
This is a feature of two’s-complement binary representation.
A simple way to understand it is that Integer.MIN_VALUE is -231 but Integer.MAX_VALUE is 231-1, so the negation of Integer.MIN_VALUE is just outside the range of int.
We should certainly include these boundary values in our testing.
We incorporate boundaries as single-element subdomains in the partition, so that the test suite will necessarily include the boundary value as a test case.
For abs, we would add subdomains for each of the relevant boundaries:
- a = 0, because
absbehaves differently on positive and negative numbers - a =
Integer.MIN_VALUE, the most negative possibleintvalue, because the spec calls out some unusual behavior there - a =
Integer.MAX_VALUE, the largest positiveintvalue, for symmetry and completeness
Our original two subdomains would then shrink to exclude the boundary values: { a | 0 < a < Integer.MAX_VALUE } and { a | Integer.MIN_VALUE < a < 0 }.
This is a now a partition of the input space of abs: the five subdomains are disjoint and completely cover the space.
One way to write it compactly looks like this:
// partition:
// a = Integer.MIN_VALUE
// Integer.MIN_VALUE < a < 0
// a = 0
// 0 < a < Integer.MAX_VALUE
// a = Integer.MAX_VALUEOur test suite might then be:
- a = 0
- a =
Integer.MIN_VALUE - a =
Integer.MAX_VALUE - a = 17 to cover the subdomain 0 < a <
Integer.MAX_VALUE - a = -3 to cover the subdomain
Integer.MIN_VALUE< a < 0`
reading exercises
For this function:
/**
* @param winsAndLosses a string of length at most 5 consisting of 'W' or 'L' characters
* @return the fraction of characters in winsAndLosses that are 'W'
*/
double winLossRatio(String winsAndLosses);Which of the following are appropriate boundary values for testing this function?
(missing explanation)
Example: BigInteger.multiply()
Let’s look at a slightly more complicated example.
BigInteger is a class built into the Java library that can represent integers of any size, unlike the primitive types int and long that have only limited ranges.
BigInteger has a method multiply that multiplies two BigInteger values together:
/**
* @param val another BigInteger
* @return a BigInteger whose value is (this * val).
*/
public BigInteger multiply(BigInteger val)For example, here’s how it might be used:
BigInteger a = new BigInteger("9500000000"); // 9.5 billion
BigInteger b = new BigInteger("2");
BigInteger ab = a.multiply(b); // should be 19 billionThis example shows that even though only one parameter is explicitly shown in the method’s declaration, multiply is actually a function of two arguments: the object you’re calling the method on (a in the example above), and the parameter that you’re passing in the parentheses (b in this example).
In Python, the object receiving the method call would be explicitly named as a parameter called self in the method declaration.
In Java, you don’t mention the receiving object in the parameters, and it’s called this instead of self.
So we should think of multiply as a function taking two inputs, each of type BigInteger, and producing one output of type BigInteger:
multiply : BigInteger × BigInteger → BigInteger
We again have a two-dimensional input space, consisting of all the pairs of integers (a,b). Thinking about how sign rules work with multiplication, we might start with these subdomains:
- a and b are both positive
- a and b are both negative
- a is positive, b is negative
- a is negative, b is positive
There are also some boundary values for multiplication that we should check:
Finally, because the purpose of BigInteger is to represent arbitrarily-large integers, we should make sure to try integers that are very big, at least bigger than the biggest long, which is roughly 263, a 19-digit decimal integer.
- a or b is small or large in magnitude (i.e., small enough to represent in a
longvalue, or too large for along)
Let’s bring all these observations together into a single partition of the whole (a,b) space. We’ll choose a and b independently from:
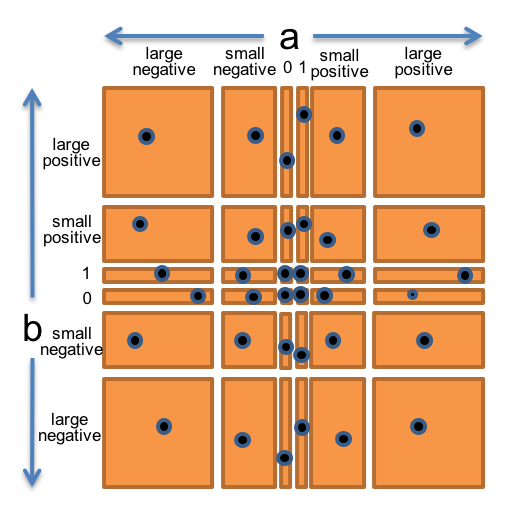
- 0
- 1
- small positive integer (≤
Long.MAX_VALUEand > 1) - small negative integer (≥
Long.MIN_VALUEand < 0) - large positive integer (>
Long.MAX_VALUE) - large negative integer (<
Long.MIN_VALUE)
So this would produce 6 × 6 = 36 subdomains that partition the space of pairs of integers.
To produce the test suite from this partition, we would pick an arbitrary pair (a,b) from each square of the grid, for example:
- (a,b) = (0, 0) to cover (0, 0)
- (a,b) = (0, 1) to cover (0, 1)
- (a,b) = (0, 8392) to cover (0, small positive integer)
- (a,b) = (0, -7) to cover (0, small negative integer)
- …
- (a,b) = (-1060, -10810) to cover (large negative, large negative)
The figure at the right shows how the two-dimensional (a,b) space is divided by this partition, and the points are test cases that we might choose to completely cover the partition.
Using multiple partitions
The examples so far used only one partition – one collection of disjoint subdomains – across the entire input space.
For functions with multiple parameters, this can become costly.
Each parameter may have interesting behavior variation and several boundary values, so forming a single partition of the input space from the Cartesian product of the behavior on each parameter leads to a combinatorial explosion in the size of the resulting test suite.
We saw this already with multiply, in which the Cartesian product partition already had 6 × 6 = 36 subdomains, requiring 36 test cases to cover.
For a function with n parameters, the Cartesian-product approach produces a test suite of size exponential in n, which quickly becomes infeasible for manual test authoring.
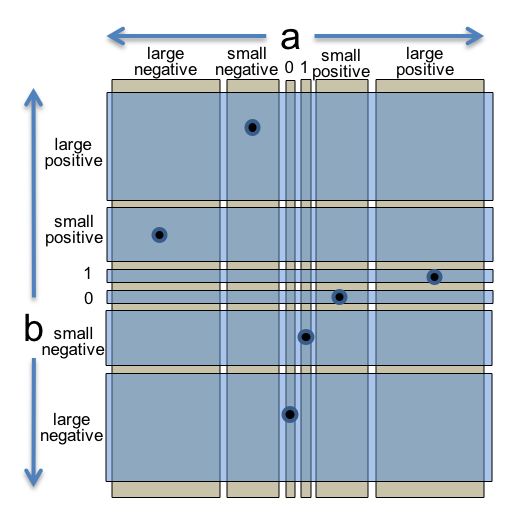
An alternative approach is to treat the features of each input a and b as two separate partitions of the input space. One partition only considers the value of a:
And the other partition only considers the value of b:
These two partitions are illustrated at the right. Every input pair (a,b) belongs to exactly one subdomain from each partition.
We might write the two partitions compactly as follows:
// partition on a:
// a = 0
// a = 1
// a is small integer > 1
// a is small integer < 0
// a is large positive integer
// a is large negative integer
// (where "small" fits in long, and "large" doesn't)
// partition on b:
// b = 0
// b = 1
// b is small integer > 1
// b is small integer < 0
// b is large positive integer
// b is large negative integerWe still want to cover every subdomain with a test case, but now a single test case can cover multiple subdomains from different partitions, making the test suite more efficient. We can cover both partitions completely with just 6 test cases, as shown on the right.
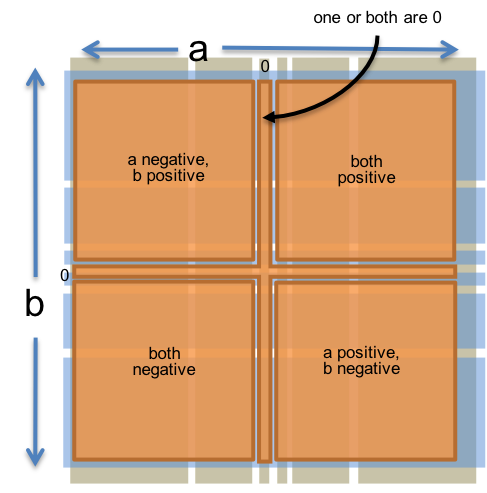
Partitioning a and b independently raises the risk that you’re no longer testing the interaction between them. For example, sign handling in multiplication is a possible source of bugs, and the sign of the result depends on the signs of both a and b. But we can add an additional partition that captures this interaction:
// partition on signs of a and b:
// a and b are both positive
// a and b are both negative
// a positive and b negative
// a negative and b positive
// one or both are 0Now we have three partitions, with 6, 6, and 5 subdomains each, but we don’t need the Cartesian product of 6 × 6 × 5 test cases to cover them. A test suite with 6 carefully-chosen test cases can cover the subdomains of all three partitions.
We can continue to add partitions this way, as we think more about the spec and observe other behavioral variations that might lead to bugs. With careful test case selection, additional partitions should require few (if any) additional test cases.
Sometimes we may want to use the Cartesian product approach on multiple partitions, to produce a more thorough test suite. But even in those cases, the Cartesian product may be smaller than we expect. When subdomains from different partitions turn out to be mutually exclusive, the Cartesian product won’t include a subdomain for that particular combination of subdomains. We’ll see an example of that in one of the exercises below.
As a starting point for test-first programming, however, a small test suite that covers each subdomain of several thoughtfully-chosen partitions strikes a good balance between size and thoroughness. The test suite may then grow further with glass box testing, code coverage measurement, and regression testing, which we’ll see later in this reading.
reading exercises
Consider this partition on a from above:
// partition on a:
// a = 0
// a = 1
// a is small integer > 1
// a is small integer < 0
// a is large positive integer
// a is large negative integer
// (where "small" fits in long, and "large" doesn't)This partition actually combines several distinct concerns: the sign of a, the magnitude of a (small or large), and the boundary values 0 and 1.
We can instead think about these concerns as independent partitions. From among the choices below, choose a subset that would be legal partitions and that together would capture the same concerns:
(missing explanation)
Consider again this partition on a from above:
// partition on a:
// a = 0
// a = 1
// a is small integer > 1
// a is small integer < 0
// a is large positive integer
// a is large negative integer
// (where "small" fits in long, and "large" doesn't)This partition has 6 subdomains, so 6 different values of a can cover it, one chosen for each subdomain.
Suppose we used these three partitions of a instead:
// partition on a: 0, positive, negative
// partition on a: 1, !=1
// partition on a: small (fits in long), large (doesn't fit in long)If we just want to cover every subdomain of the three partitions, how many different values of a would we need?
(missing explanation)
If we want to cover the Cartesian product of these three partitions, how many different values of a would we need?
(missing explanation)
It is sometimes convenient to think about and write an input space partition in terms of the output of the function, because variations in behavior may be more visible there. For example:
// partition on a.multiply(b): 0, positive, negativeis shorthand for the three-subdomain partition consisting of:
{ (a,b) | a.multiply(b) = 0 }
{ (a,b) | a.multiply(b) > 0 }
{ (a,b) | a.multiply(b) < 0 }
Using this approach, how many test cases are needed to cover the following three partitions?
// partition on a: 0, positive, negative
// partition on b: 0, positive, negative
// partition on a.multiply(b): 0, positive, negative(missing explanation)
How many are needed to cover the following two partitions?
// partition on value of abs(x): same as x, different from x
// partition on sign of abs(x): 0, positive, negativeNote that the second partition is correct, because as mentioned above, Math.abs(x) can indeed return a negative integer.
(missing explanation)
Consider the following specification:
/**
* Reverses the end of a string.
*
* 012345 012345
* For example: reverseEnd("Hello, world", 5) returns "Hellodlrow ,"
* <-----> <----->
*
* With start == 0, reverses the entire text.
* With start == text.length(), reverses nothing.
*
* @param text string that will have its end reversed
* @param start the index at which the remainder of the input is reversed,
* requires 0 <= start <= text.length()
* @return input text with the substring from start to the end of the string reversed
*/
public static String reverseEnd(String text, int start)Which of the following are reasonable partitions for the start parameter?
(missing explanation)
Which of the following are reasonable partitions for the text parameter?
(missing explanation)
Automated unit testing with JUnit
A well-tested program will have tests for every individual module that it contains. A test that tests an individual module, in isolation if possible, is called a unit test.
JUnit is a widely-adopted Java unit testing library, and we will use it heavily in 6.031.
A JUnit unit test is written as a method preceded by the annotation @Test.
A unit test method typically contains one or more calls to the module being tested, and then checks the results using assertion methods like assertEquals, assertTrue, and assertFalse.
For example, the tests we chose for max above might look like this when implemented for JUnit:
public class MaxTest {
...
@Test
public void testALessThanB() {
assertEquals(2, Math.max(1, 2));
}
@Test
public void testBothEqual() {
assertEquals(9, Math.max(9, 9));
}
@Test
public void testAGreaterThanB() {
assertEquals(10, Math.max(10, -9));
}
}Note that the order of the parameters to assertEquals is important.
The first parameter should be the expected result, usually a constant, that the test wants to see.
The second parameter is the actual result, what the code actually does.
If you switch them around, then JUnit will produce a confusing error message when the test fails.
All JUnit assertions that compare values follow this order consistently: expected first, actual second.
An assertion can also take an optional message string as the last argument, which you can use to make the test failure clearer.
If an assertion in a test method fails, then that test method returns immediately, and JUnit records a failure for that test.
A test class can contain any number of @Test methods, which are run independently when you run the test class with JUnit.
Even if one test method fails, the others will still be run.
reading exercises
Consider this JUnit test, which is intended to test a method pickRandomly() that picks a random number from its input set:
@Test
public void testDrawFromSet() {
Set<Integer> set = Set.of(293, 384, 10, 5, -3, 99);
int result = pickRandomly(set);
ASSERTION HERE
}Which assertion, put where the code says ASSERTION HERE, would be both correct and useful for debugging?
(missing explanation)
Documenting your testing strategy
It’s a good idea to write down the testing strategy you used to create a test suite: the partitions, their subdomains, and which subdomains each test case was chosen to cover. Writing down the strategy makes the thoroughness of your test suite much more visible to the reader.
Document the partitions and subdomains in a comment at the top of the JUnit test class.
For example, to document our strategy for testing max, we would write this in MaxTest.java:
public class MaxTest {
/*
* Testing strategy
*
* partition:
* a < b
* a > b
* a = b
*/Each test case should have a comment above it saying which subdomain(s) it covers, e.g.:
// covers a < b
@Test
public void testALessThanB() {
assertEquals(2, Math.max(1, 2));
}Most test suites will have more than one partition, and most test cases will cover multiple subdomains.
For example, here’s a strategy for multiply, using seven partitions:
public class Multiply {
/*
* Testing strategy
*
* cover the cartesian product of these partitions:
* partition on a: positive, negative, 0
* partition on b: positive, negative, 0
* partition on a: 1, !=1
* partition on b: 1, !=1
* partition on a: small (fits in a long value), or large (doesn't fit)
* partition on b: small, large
*
* cover the subdomains of these partitions:
* partition on signs of a and b:
* both positive
* both negative
* different signs
* one or both are 0
*/Then every test case has a comment identifying the subdomains that it was chosen to cover, e.g.:
// covers a is positive, b is negative,
// a fits in long value, b fits in long value,
// a and b have different signs
@Test
public void testDifferentSigns() {
assertEquals(BigInteger.valueOf(-146), BigInteger.valueOf(73).multiply(BigInteger.valueOf(-2)));
}
// covers a = 1, b != 1, a and b have same sign
@Test
public void testIdentity() {
assertEquals(BigInteger.valueOf(33), BigInteger.valueOf(1).multiply(BigInteger.valueOf(33)));
}reading exercises
Suppose you are writing a test suite for the max(int a, int b) method in Math.java.
By convention you put your JUnit tests in another file MathTest.java.
Where does each of these pieces of your testing documentation go?
(missing explanation)
(missing explanation)
(missing explanation)
(missing explanation)
Black box and glass box testing
Recall from above that the specification is the description of the function’s behavior — the types of parameters, type of return value, and constraints and relationships between them.
Black box testing means choosing test cases only from the specification, not the implementation of the function.
That’s what we’ve been doing in our examples so far.
We partitioned and looked for boundaries in abs, max, and multiply without looking at the actual code for these functions.
In fact, following the test-first programming approach, we hadn’t even written the code for these functions yet.
Glass box testing means choosing test cases with knowledge of how the function is actually implemented. For example, if the implementation selects different algorithms depending on the input, then you should partition around the points where different algorithms are chosen. If the implementation keeps an internal cache that remembers the answers to previous inputs, then you should test repeated inputs.
For the case of BigInteger.multiply, when we finally implemented it, we may have decided to represent small integers with int values and large integers with a list of decimal digits.
This decision introduces new boundary values, presumably at Integer.MAX_VALUE and Integer.MIN_VALUE, and a new partition around them.
When doing glass box testing, you must take care that your test cases don’t require specific implementation behavior that isn’t specifically called for by the spec. For example, if the spec says “throws an exception if the input is poorly formatted,” then your test shouldn’t check specifically for a NullPointerException just because that’s what the current implementation does. The specification in this case allows any exception to be thrown, so your test case should likewise be general in order to be correct, and preserve the implementor’s freedom. We’ll have much more to say about this in the class on specs.
reading exercises
Consider the following function:
/**
* Sort a list of integers in nondecreasing order. Modifies the list so that
* values.get(i) <= values.get(i+1) for all 0<=i<values.size()-1
*/
public static void sort(List<Integer> values) {
// choose a good algorithm for the size of the list
if (values.size() < 10) {
radixSort(values);
} else if (values.size() < 1000*1000*1000) {
quickSort(values);
} else {
mergeSort(values);
}
}Which of the following test cases are likely to be boundary values produced by glass box testing?
(missing explanation)
Coverage
One way to judge a test suite is to ask how thoroughly it exercises the program. This notion is called coverage. Here are three common kinds of coverage:
- Statement coverage: is every statement run by some test case?
- Branch coverage: for every
iforwhilestatement in the program, are both the true and the false direction taken by some test case? - Path coverage: is every possible combination of branches — every path through the program — taken by some test case?
Branch coverage is stronger (requires more tests to achieve) than statement coverage, and path coverage is stronger than branch coverage. In industry, 100% statement coverage is a common goal, but even that is rarely achieved due to unreachable defensive code (like “should never get here” assertions). 100% branch coverage is highly desirable, and safety critical industry code has even more arduous criteria (e.g., MC/DC, modified condition/decision coverage). Unfortunately 100% path coverage is infeasible, requiring exponential-size test suites to achieve.
A standard approach to testing is to add tests until the test suite achieves adequate statement coverage: i.e., so that every reachable statement in the program is executed by at least one test case. In practice, statement coverage is usually measured by a code coverage tool, which counts the number of times each statement is run by your test suite. With such a tool, glass box testing is easy; you just measure the coverage of your black box tests, and add more test cases until all important statements are logged as executed.
A good code coverage tool for Eclipse is EclEmma, shown on the right.
In EclEmma, a line that has been executed by the test suite is colored green, and a line not yet covered is red.
A line containing a branch that has been executed in only one direction – always true but never false, or vice versa – is colored yellow.
If you saw the result on the right from your coverage tool, your next step would be to come up with a test case that causes the if test to be true at least once, and add it to your test suite so that the yellow and red lines become green.
When EclEmma is installed (as it is in the 6.031 Eclipse installation), you can get code coverage highlighting using Run → Coverage As.
reading exercises
You should already have EclEmma installed in Eclipse on your laptop.
Then create a new Java class called Hailstone.java (you can make a new project for it, or just put it in the project from class 2 exercises) containing this code:
public class Hailstone {
public static void main(String[] args) {
int n = 3;
while (n != 1) {
if (n % 2 == 0) {
n = n / 2;
} else {
n = 3 * n + 1;
}
}
}
}Run this class with EclEmma code coverage highlighting turned on, by choosing Run → Coverage As → Java Application.
By changing the initial value of n, you can observe how EclEmma highlights different lines of code differently.
(missing explanation)
(missing explanation)
(missing explanation)
Unit and integration testing
We’ve so far been talking about unit tests that test a single module in isolation. Testing modules in isolation leads to much easier debugging. When a unit test for a module fails, you can be more confident that the bug is found in that module, rather than anywhere in the program.
In contrast to a unit test, an integration test tests a combination of modules, or even the entire program. If all you have are integration tests, then when a test fails, you have to hunt for the bug. It might be anywhere in the program. Integration tests are still important, because a program can fail at the connections between modules. For example, one module may be expecting different inputs than it’s actually getting from another module. But if you have a thorough set of unit tests that give you confidence in the correctness of individual modules, then you’ll have much less searching to do to find the bug.
Suppose you’re building a document search engine.
Two of your modules might be load(), which loads a file, and extract(), which splits a document into its component words:
/**
* @return the contents of the file
*/
public static String load(File file) { ... }
/**
* @return the words in string s, in the order they appear,
* where a word is a contiguous sequence of
* non-whitespace and non-punctuation characters
*/
public static List<String> extract(String s) { ... }These methods might be used by another module index() to make the search engine’s index:
/**
* @return an index mapping a word to the set of files
* containing that word, for all files in the input set
*/
public static Map<String, Set<File>> index(Set<File> files) {
...
for (File file : files) {
String doc = load(file);
List<String> words = extract(doc);
...
}
...
} In our test suite, we would want:
- unit tests just for
loadthat test it on various files - unit tests just for
extractthat test it on various strings - unit tests for
indexthat test it on various sets of files
One mistake that programmers sometimes make is writing test cases for extract in such a way that the test cases depend on load to be correct.
For example, a test case might use load to load a file, and then pass its result as input to extract.
But this is not a unit test of extract.
If the test case fails, then we don’t know if the failure is due to a bug in load or extract.
It’s better to think about and test extract in isolation.
Using test partitions that involve realistic file content might be reasonable, because that’s how extract is actually used in the program.
But don’t actually call load from the test case, because load may be buggy!
Instead, store file content as a literal string, and pass it directly to extract.
That way you’re writing an isolated unit test, and if it fails, you can be more confident that the bug is in the module it’s actually testing.
Note that the unit tests for index can’t easily be isolated in this way.
When a test case calls index, it is testing the correctness of not only the code inside index, but also all the methods called by index.
If the test fails, the bug might be in any of those methods.
That’s why we want separate tests for load and extract, to increase our confidence in those modules individually and localize the problem to the index code that connects them together.
Isolating a higher-level module like index is possible if we write stub versions of the modules that it calls.
For example, a stub for load wouldn’t access the filesystem at all, but instead would return mock file content no matter what File was passed to it.
A stub for a class is often called a mock object.
Stubs are an important technique when building large systems, but we will generally not use them in 6.031.
reading exercises
Suppose you are developing a new pizza recipe. Making pizza involves three “modules” (subrecipes) for:
You make the dough for the crust, bake it by itself, and see how crunchy and tasty it comes out. This is:
(missing explanation)
You decide to buy a premade spice mix from a specialty store. You make a sauce using the spices, then taste it. This is:
(missing explanation)
You put sauce and toppings on a crust and bake it, to see whether the crust still cooks well with the moist stuff on top of it. This is:
(missing explanation)
Automated regression testing
Nothing makes tests easier to run, and more likely to be run, than complete automation. Automated testing means running the tests and checking their results automatically.
The code that runs tests on a module is a test driver (also known as a test harness or test runner). A test driver should not be an interactive program that prompts you for inputs and prints out results for you to manually check. Instead, a test driver should invoke the module itself on fixed test cases and automatically check that the results are correct. The result of the test driver should be either “all tests OK” or “these tests failed: …” A good testing framework, like JUnit, allows you to build and run this kind of test driver, with a suite of automated tests.
Note that automated testing frameworks like JUnit make it easy to run the tests, but you still have to come up with good test cases yourself. Automatic test generation is a hard problem, still a subject of active computer science research.
Once you have test automation, it’s very important to rerun your tests when you modify your code. Software engineers know from painful experience that any change to a large or complex program is dangerous. Whether you’re fixing another bug, adding a new feature, or optimizing the code to make it faster, an automated test suite that preserves a baseline of correct behavior – even if it’s only a few tests – will save your bacon. Running the tests frequently while you’re changing the code prevents your program from regressing — introducing other bugs when you fix new bugs or add new features. Running all your tests after every change is called regression testing.
Whenever you find and fix a bug, take the input that elicited the bug and add it to your automated test suite as a test case. This kind of test case is called a regression test. This helps to populate your test suite with good test cases. Remember that a test is good if it elicits a bug — and every regression test did in one version of your code! Saving regression tests also protects against reversions that reintroduce the bug. The bug may be an easy error to make, since it happened once already.
This idea also leads to test-first debugging. When a bug arises, immediately write a test case for it that elicits it, and immediately add it to your test suite. Once you find and fix the bug, all your test cases will be passing, and you’ll be done with debugging and have a regression test for that bug.
In practice, these two ideas, automated testing and regression testing, are almost always used in combination. Regression testing is only practical if the tests can be run often, automatically. Conversely, if you already have automated testing in place for your project, then you might as well use it to prevent regressions. So automated regression testing is a best-practice of modern software engineering.
Iterative test-first programming
Let’s revisit the test-first programming idea that we introduced at the start of this reading, and refine it. Effective software engineering does not follow a linear process. Practice iterative test-first programming, in which you are prepared to go back and revise your work in previous steps:
- Write a specification for the function.
- Write tests that exercise the spec. As you find problems, iterate on the spec and the tests.
- Write an implementation. As you find problems, iterate on the spec, the tests, and the implementation.
Each step helps to validate the previous steps. Writing tests is a good way to understand the specification. The specification can be incorrect, incomplete, ambiguous, or missing corner cases. Trying to write tests can uncover these problems early, before you’ve wasted time working on an implementation of a buggy spec. Similarly, writing the implementation may help you discover missing or incorrect tests, or prompt you to revisit and revise the specification.
Since it may be necessary to iterate on previous steps, it doesn’t make sense to devote enormous amounts of time making one step perfect before moving on to the next step. Plan for iteration:
For a large specification, start by writing only one part of the spec, proceed to test and implement that part, then iterate with a more complete spec.
For a complex test suite, start by choosing a few important partitions, and create a small test suite for them. Proceed with a simple implementation that passes those tests, and then iterate on the test suite with more partitions.
For a tricky implementation, first write a simple brute-force implementation that tests your spec and validates your test suite. Then move on to the harder implementation with confidence that your spec is good and your tests are correct.
Iteration is a feature of every modern software engineering process (such as Agile and Scrum), with good empirical support for its effectiveness. Iteration requires a different mindset than you may be used to as a student solving homework and exam problems. Instead of trying to solve a problem perfectly from start to finish, iteration means reaching a rough solution as soon as possible, and then steadily refining and improving it, so that you have time to discard and rework if necessary. Iteration makes the best use of your time when a problem is difficult and the solution space is unknown.
reading exercises
Suppose you are writing a binary-search method, and you are expected to provide not only a working implementation but also a clear spec for clients and a useful test suite as well.
Although binary search is a straightfoward algorithm to understand, it is notoriously tricky to implement correctly, so you are looking for all the help you can get to make sure you get it right.
Which of these steps will help validate your specification, before you implement the binary-search algorithm?
(missing explanation)
Which of these steps will help validate your test suite, before you implement the binary-search algorithm?
(missing explanation)
Why is it good to find and remove bugs in your spec and test suite before starting the tricky implementation?
(missing explanation)
Summary
In this reading, we saw these ideas:
- Test-first programming. Write tests before you write code.
- Systematic testing with partitioning and boundary values, to design a test suite that is correct, thorough, and small.
- Glass box testing and statement coverage for filling out a test suite.
- Unit-testing each module, in isolation as much as possible.
- Automated regression testing to keep bugs from coming back.
- Iterative development. Plan to redo some work.
The topics of today’s reading connect to our three key properties of good software as follows:
Safe from bugs. Testing is about finding bugs in your code, and test-first programming is about finding them as early as possible, right after you introduce them.
Easy to understand. Systematic testing with a documented testing strategy makes it easier to understand how test cases were chosen and how thorough a test suite is.
Ready for change. Correct test suites only depend on behavior in the spec, which allows the implementation to change within the confines of the spec. We also talked about automated regression testing, which helps keep bugs from coming back when changes are made to code.
An exercise for the reader
At this point you should have completed all the reading exercises above.
Completing the reading exercises prepares you for the nanoquiz at the beginning of each class meeting, and submitting the exercises is required by 10:00pm MIT time the evening before class.
At this point you should have also completed these levels of the Java Tutor:

