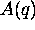, by computing the Fourier
transform of the wave packet in x-space. The Fourier transform is
defined in terms of continuous variables x and q. To implement
this in Matlab we need to approximate
We find the expansion coefficients, 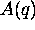, by computing the Fourier
transform of the wave packet in x-space. The Fourier transform is
defined in terms of continuous variables x and q. To implement
this in Matlab we need to approximate
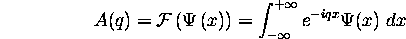
by use of the discrete equation
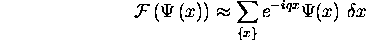
To do this, we create a vector with all of our x values, i.e.:
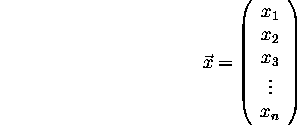
Similarly, we define a vector with all the values of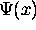 
:
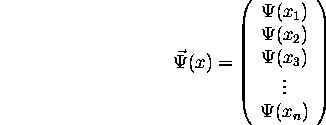
We then define a vector for our reciprocal space:
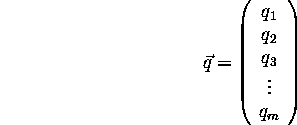
The values for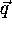 
are determined by the properties
of the discrete Fourier transform. Note,
in general,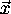 
and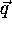 
do not contain the same number of
elements, i.e.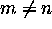 
.
Now, the outer product of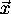 
and 
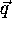is
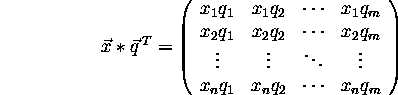
Taking the exponential of i times each element of the above matrix yields:
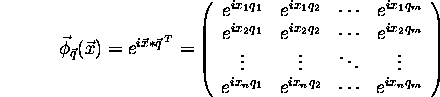
Note, the Matlab command `` exp'' takes the exponent of each element in a matrix. Then,
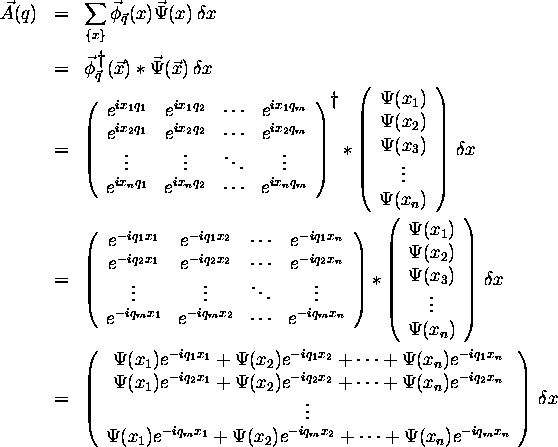
i.e. a vector indexed by q which contains the sum we defined to be an approximation to the Fourier transform, known as the Discrete Fourier Transform (DFT).