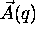 , how do we find the time dependence of
, how do we find the time dependence of
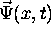 ? Since
? Since 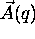 is the coefficient vector for
the eigenfunctions of
is the coefficient vector for
the eigenfunctions of 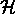 , we know the time dependence is
accounted for by multiplying each coefficient by
, we know the time dependence is
accounted for by multiplying each coefficient by 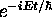 . So, we now create a
vector E, indexed by q.
. So, we now create a
vector E, indexed by q.
Now that we have 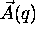 , how do we find the time dependence of
, how do we find the time dependence of
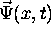 ? Since
? Since 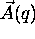 is the coefficient vector for
the eigenfunctions of
is the coefficient vector for
the eigenfunctions of 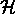 , we know the time dependence is
accounted for by multiplying each coefficient by
, we know the time dependence is
accounted for by multiplying each coefficient by 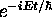 . So, we now create a
vector E, indexed by q.
. So, we now create a
vector E, indexed by q.
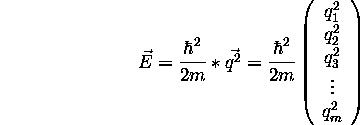
Now, if we take the exponential of 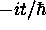 times each element, where t
is the time we wish to evaluate
times each element, where t
is the time we wish to evaluate 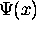 at, we get
at, we get
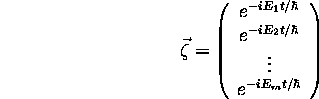
Now, if we perform element by element multiplication ( Matlab command is ``  '') on
'') on
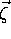 (q) and
(q) and 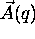 we get:
we get:
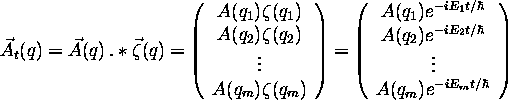
Now, we have taken account for the time dependence by modifying our
amplitude function (note the subscript t to denote that this is
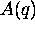 at a particular time t). The last chore is to now compute the
wave function in x-space from the modified amplitude function.
at a particular time t). The last chore is to now compute the
wave function in x-space from the modified amplitude function.