Diblock Copolymers
Finally, we will see how many of the ideas presented in the preceding sections can be applied in the analysis of diblock copolymers. It will become clear that universality makes it possible to think about phase transitions in an abstract manner and develop novel and experimentally verifiable conclusions based on a general understanding of the principles and mechanics underlying phase transitions.
A diblock copolymer is a polymer consisting of two types of monomers, A and B. The monomers are arranged such that there is a chain of each monomer, and those two chains are grafted together to form a single copolymer chain. A large collection of diblock copolymers is called a polymer melt, and below a certain temperature this melt will exhibit a phase transition. Above the transition temperature the amount of A and B is equally distributed throughout the material. This is the disordered state of the material and exhibits no spatial variance, and thus possesses the same type of translational symmetry found in liquids.
As with any thermodynamic system there is a competition between entropy and enthalpy which can be expressed as the minimization of a free energy. At high temperatures when entropy dominates the polymer melt is highly disordered and the distribution of A and B is even within fluctuation around mean zero. Below a certain transition temperature the polymer melt orders. The ordering results in the formation of a periodic distribution of A and B, and many exotic geometries have been observed in experiment. Below the transition temperature, however, the monomer segments will segregate and form regular, periodic structures. That is, the A and B segments of each copolymer chain will come together and display macroscopic order. Some of the common shapes that have been observed experimentally are lines (lamellar), hexagonal cylinders, and stacked balls (body centered cubic, BCC). Copolymers are important as a class of materials because they can be engineered to exhibit specific physical properties. Each geometry could potentially possess different physical characteristics, and thus the ability to readily switch between the phases could allow for materials with tunable properties. The various phases of a diblock copolymer melt can be succinctly described by a phase diagram. Unlike the previously shown phase diagrams, temperature is no longer an explicit parameter. Rather, the two parameters that define the phase diagram are the Flory parameter, which is a measure of the strength of interactions between monomers (alike and different) and the bulk fraction of monomer A. The Flory parameter is temperature dependent in a non-trivial manner, but since it is a monotonic function of temperature, the phase diagram qualitatively says all the same things that a diagram that had temperature explicitly would. The bulk fraction f is quite literally the fraction of A monomer to total monomer in the melt.
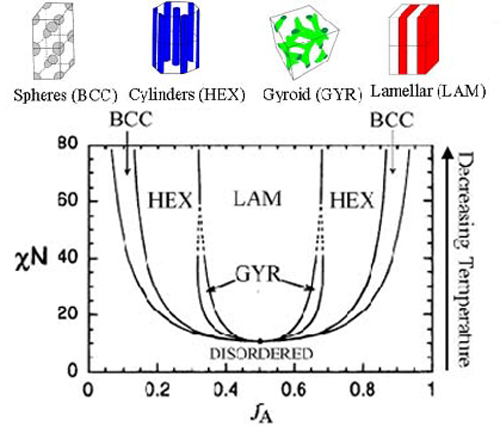
This is the phase diagram for a block copolymer melt including an additional gyroidal phase. The parameter on the y axis is the Flory parameter (chi) multiplied by N, the number of statistical segments in a copolymer chain. A statistical segment is like the number of monomers that when taken as a unit would make the polymer appear as though it were an idealized chain. It is related to the mass of a monomer and the stiffness of the chain. It is the product of chi and N which is relevant to mapping out the phase diagram.
Much like the solidification of a liquid, the phase transition is first order and loses translational symmetry in the appearance of regular periodic structure. The order parameter is the difference between the local fraction of A, and the bulk fraction. In the disordered state the order parameter is zero everywhere since the entire melt is homogenous, but in the ordered phase the order parameter is spatially varying with a periodicity.

This is another image of a diblock copolymer melt in the lamellar phase. While the spatial correlation is not infinite, as there still is some variability in the lengths and angles with which the layers form, there is high and obvious correlation.
One of the ways by which experimentalists map out the phase diagrams is by looking at the way that x-rays or neutrons are scattered off the copolymer melt as it passes through a phase transition. At the transition temperature the scattering will be particularly high and will be related to the divergence of the susceptibility, thermodynamic variable.
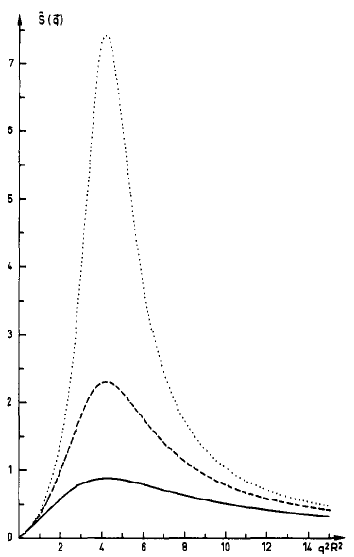
This shows the sharp rise in the susceptibility as a function of the scattering wavenumber q. As the system approaches a phase transition the peak grows relative to the rest of the curve until the transition temperature when it will go to infinity. In this case the parameter alpha is 1.
There are other varieties of copolymer melts as well. A simple extension is the triblock, or n-block copolymer, which consists of a copolymer chain consisting of n different monomer chains. There is also the example of the randomly grafted copolymer (RGC). The RGC consists of a 'backbone' of polymer A with chains of polymer B attached to it at locations randomly distributed on the backbone. Unlike the case of the diblock copolymer, which could be understood in terms of two parameters, there are three parameters necessary to describe the characteristics of an RGC melt. N is the length of the polymer backbone, m is the length of the branches it possesses, and p is the number of such branches. The locations of the branches, although they can be located anywhere along the polymer backbone, are in essence fixed from one polymer to the next. The placement of the branches are thus an example of quenched randomness. The degree of freedom for each polymer chain as described by the locations of the branch points is not free, but is fixed. Special care must be taken with such problems which are often lead to intractable calculations where particular approximations must be made.


