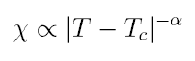Criticality
At the critical point, a number of important events occur, regardless of the nature of the material. Physicists gain enormous insight when studying a material undergoing a phase transition at its critical point. At the critical point the material exhibits an important property called universality. Universality means that the phase transition will have specific characteristics in common with other materials at the phase transition. In passing from a disordered to an ordered phase, a material will exhibit the following properties
Perhaps the most important property is the development of long range order. The previously disordered system, with no correlation between the interacting atoms, develops high correlation. In a disordered magnet the spins are pointing in every direction, and thus on average the material has no magnetization. Below the Curie temperature all the spins are aligned and the magnet has a finite magnetization. Similarly, the molecules in a liquid crystal are randomly oriented, but below the transition temperature align. Liquid crystals have a second phase transition where in addition to being aligned orientationally (pointing in the same direction) also align spatially (sit next to one another in a regular ordered fashion).
When a system transitions from one phase to another, it loses or gains symmetry. A symmetry of a system is a transformation imposed on the system that will leave it invariant, or, the same. This transformation can be a spatial or temporal translation, a rotation, or a mathematical symmetry like gauge invariance. The loss of a symmetry is known as symmetry breaking. A liquid displays spatial invariance, meaning that it appears identical everywhere. When water becomes ice and the material crystallizes, the atoms align and their dipole chooses a particular (random) direction, thus breaking the previously exhibited translational symmetry. This random choice of a direction is known as spontaneous symmetry breaking. Similarly, a disordered Ising magnet has rotational, or reflection symmetry which is lost upon the transition to an ordered state where one of two equivalent ground states is randomly chosen.
When the symmetry is lost, it can be said that it is replaced by a collective mode. This is a means by which many previously non-interacting atoms can act together. Sound waves are an example of collective modes in a solid. Oscillations are collective modes because they require many atoms which may be separated by great distances (on an atomic scale) to vibrate at the exact same frequency and phase. These are also called coherent excitations, and in the case of the breaking of a continuous symmetry, the collective modes are known as Goldstone bosons.

A spin wave is the slow variation of the magnetic dipoles in an ordered magnetic material. This is the low temperature excitation that emerges in the ordered phase.
A phase transition is also marked by the appearance of an order parameter. The order parameter is something physicists use to describe phase transitions, and quite simply is a quantity that exists in one phase (usually the low temperature phase) and disappears in the other (high temperature) phase. The magnetization in a magnet, the density in a solid/liquid/gas transition, and the orientation of the molecules in a liquid crystal are all examples of order parameters. The order parameter is related to whether the phase transition is first or second order. So-called second order, or 'continuous' phase transitions do not possess a latent heat like first order transitions. Whether the transition is first or second order is related to fundamental attributes of the system.
An important attribute of phase transitions is the divergence of certain thermodynamic properties at the critical point. Divergence means that the thermodynamic property suffers a discontinuity and changes drastically from its value in the disordered state. This is qualitatively related to the appearance of long range order, and by measuring the values of these thermodynamic variables during the phase transition, many important properties of the transition can be assessed.
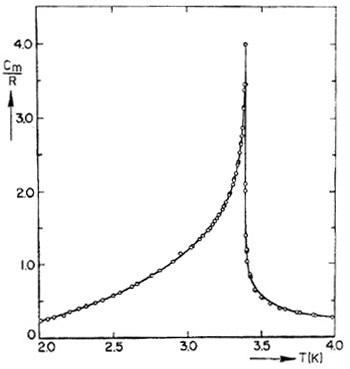
This is an example of the divergence of the heat capacity when a material undergoes a phase transition. The rate at which the heat capacity changes with temperature near the phase transition gives important insight into the nature of the phase transition and its relation to transitions in the same universality class.
The divergence of thermodynamic properties like the susceptibility and the correlation length are related to the scale invariance that defines a material at the critical point. Whereas the only length scale that defined the system before the critical point was the atomic spacing, at the critical point all length scales become important and the material takes on fractilinear character. Consider the aforementioned example of percolation. If paths of any length are possible, then zooming away from the material, the distribution of paths lengths relative to the observation scale would not change, and the material exhibits scale invariance.
The divergence of thermodynamic quantities is of particular importance as the divergence has a singular dependence on temperature of the form
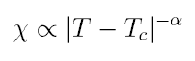
Where alpha is a positive constant. Many materials will have the same constant and diverge the same way with temperature. This is another example of universality.