The flavor text of the puzzle is:
In Patriots’ Day Town, everyone roots for New England and uses graphs to analyze their play.
Solvers need to resist any urge they might have to interpret graphs in the sense of an x–y plot of the polynomials—that’s not what they are meant to do.
First, solvers should find all the roots of the polynomials (via programming, or any number of symbolic algebra packages, or by hand if they are masochists). They will discover something interesting: each polynomial has three distinct integral roots, and every root is shared by exactly two polynomials. Most of the roots are positive integers, but there are also some negatives.
The negative roots are the integers from [-38, -1] with no gaps. The positive roots are also mostly consecutive, but there are some gaps of length one. Counting the lengths of the runs of consecutive roots (between gaps) in order yields the following sequence:
14, 1, 13, 5, 19, 6, 15, 18, 20, 8, 5, 7, 18, 1, 16, 8, 19
Interpreting these numbers as alphabetic indices spells the message:
NAMES FOR THE GRAPHS
which is an instruction telling solvers to find out what the graphs are named. But what graphs are they supposed to look at?
Solvers need to think about combinatorial graphs rather than x–y plots. Each polynomial corresponds to a vertex in a graph, with an edge between two vertices if they share a root. Since each graph has exactly three roots, the resulting graph will be a 3-regular, or cubic graph. If solvers look at the connectivity pattern among the vertices, they will observe that the full configuration separates by connected components into ten different cubic graphs.
All ten graphs are instances of well-known named graphs. Solvers may need to work out some simple graph isomorphism problems to figure out the which graph from the polynomials is which named graph. This can be accomplished by looking at the number of nodes/edges, visualizing the graphs laid out on the plane and staring at the output, writing code, etc.
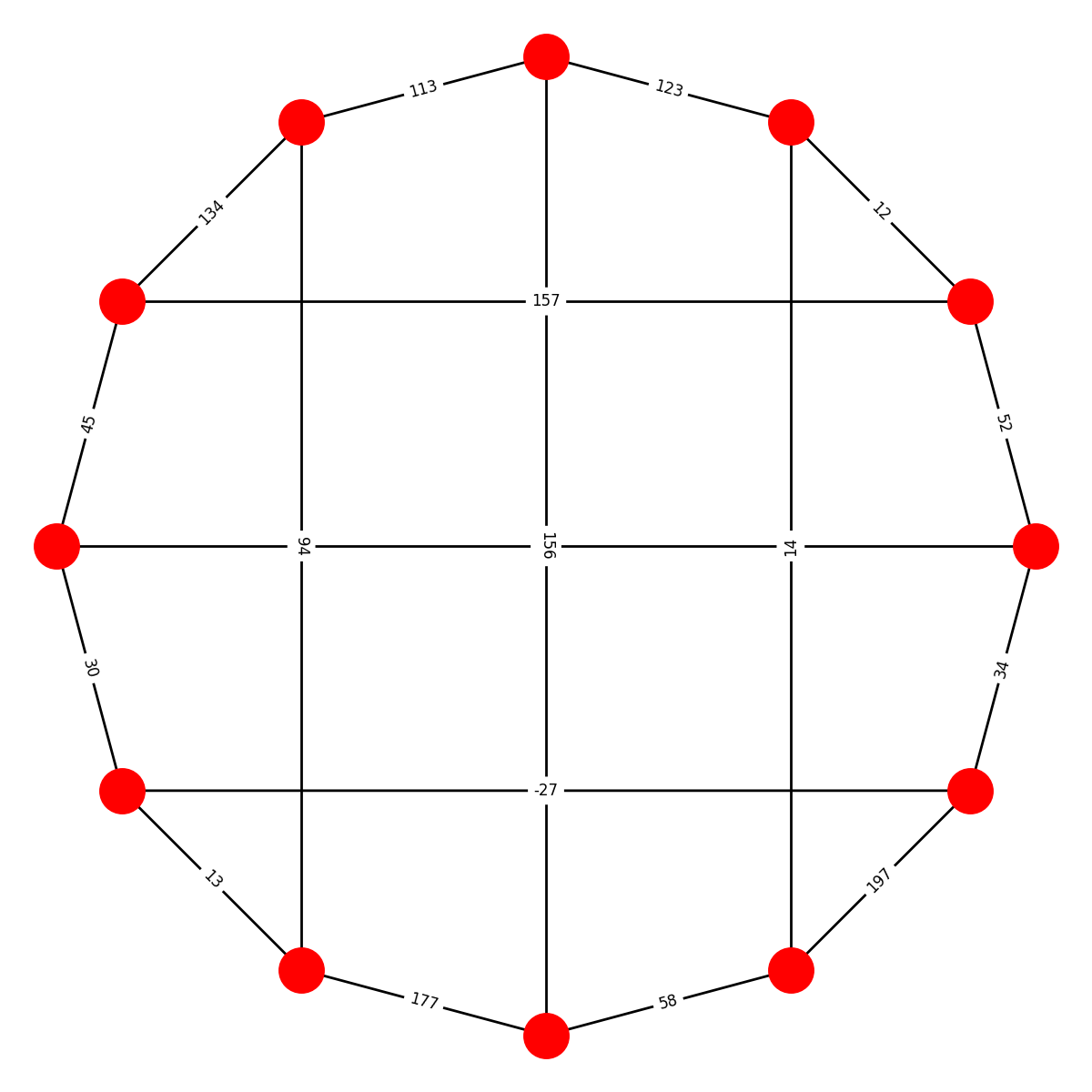
Here are the ten graphs and their names; edges are labeled with the values of the shared roots. (Apologies that some of the edge labels are obscured and that some layouts are a bit wonky):
BIDIAKIS CUBE
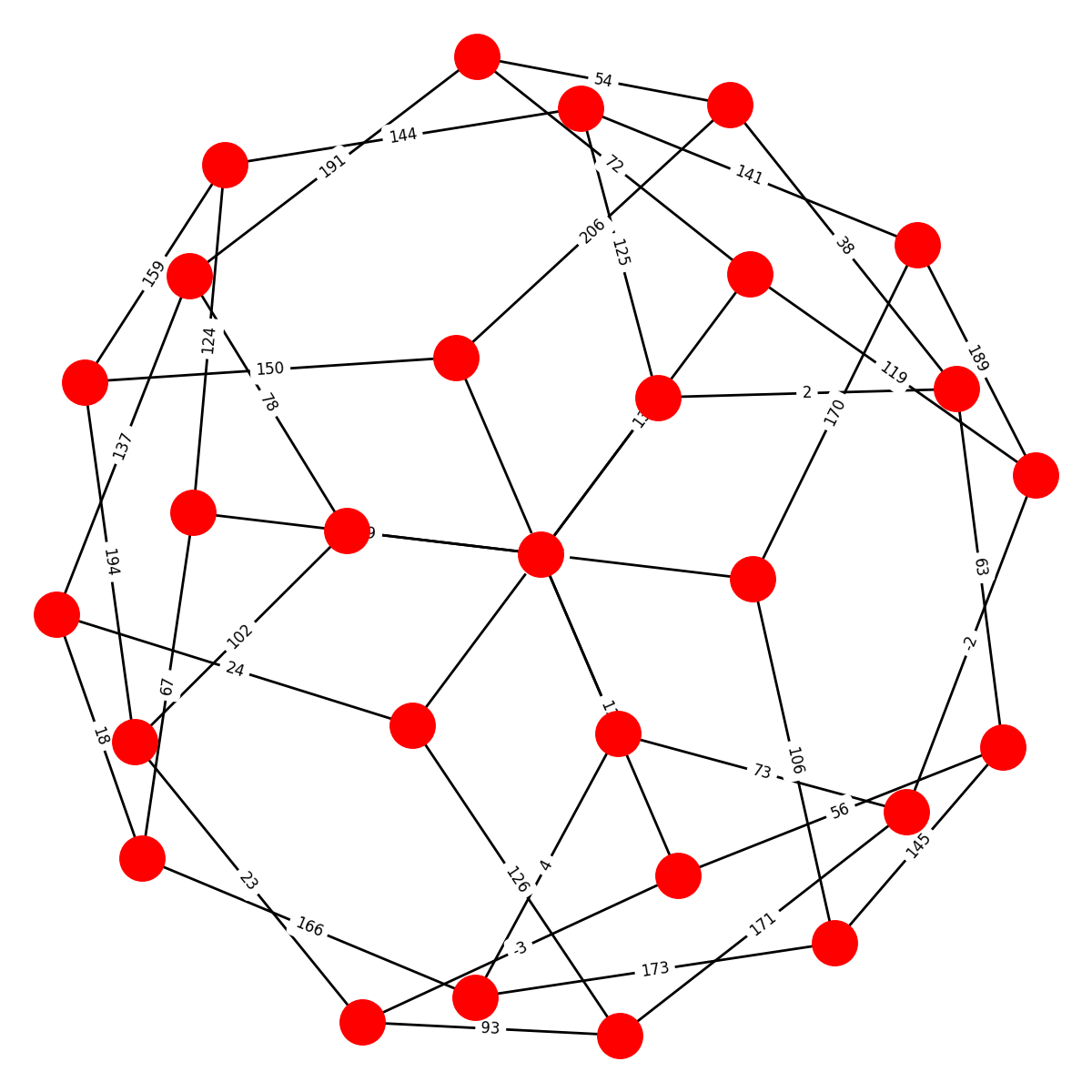
COXETER
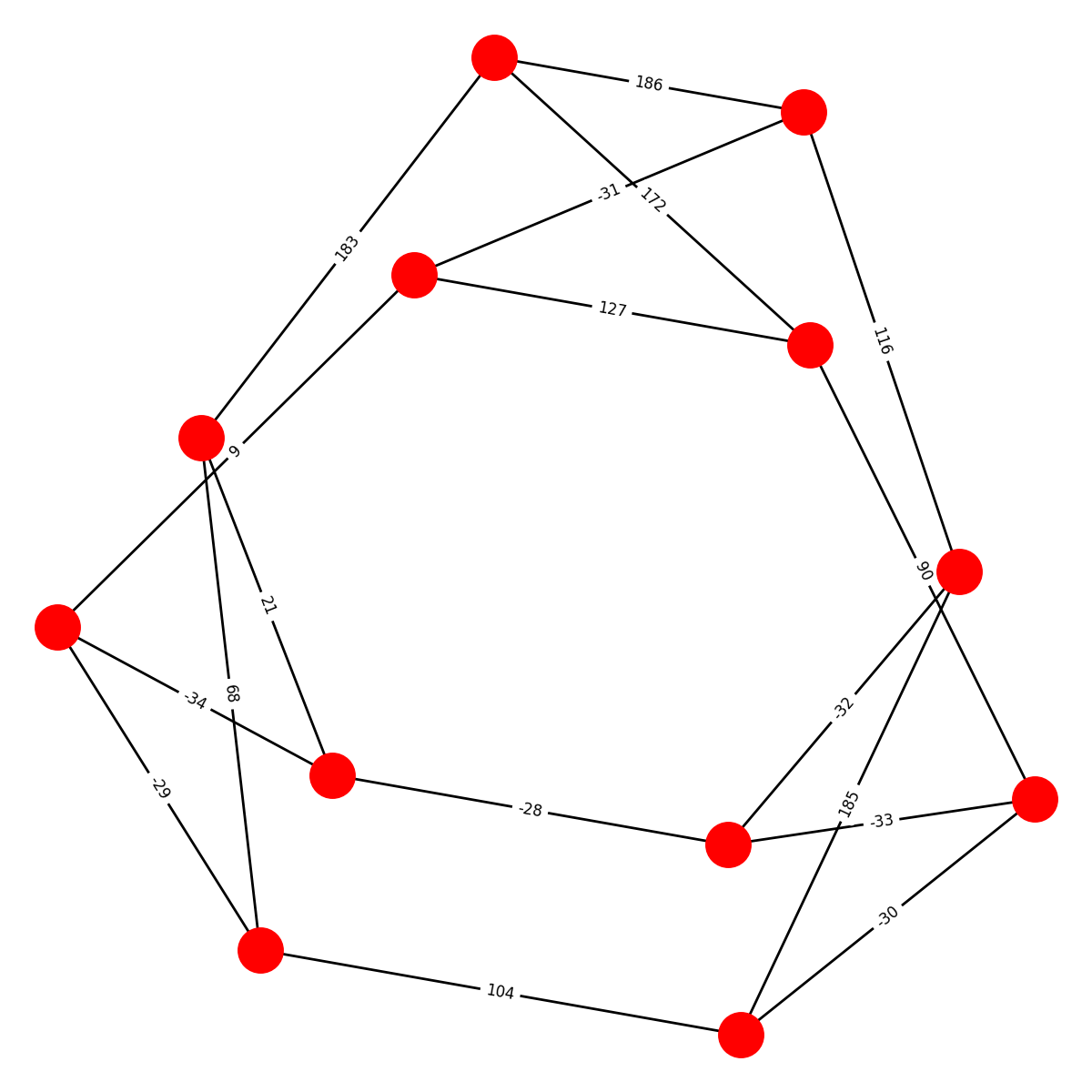
FRANKLIN
FRUCHT
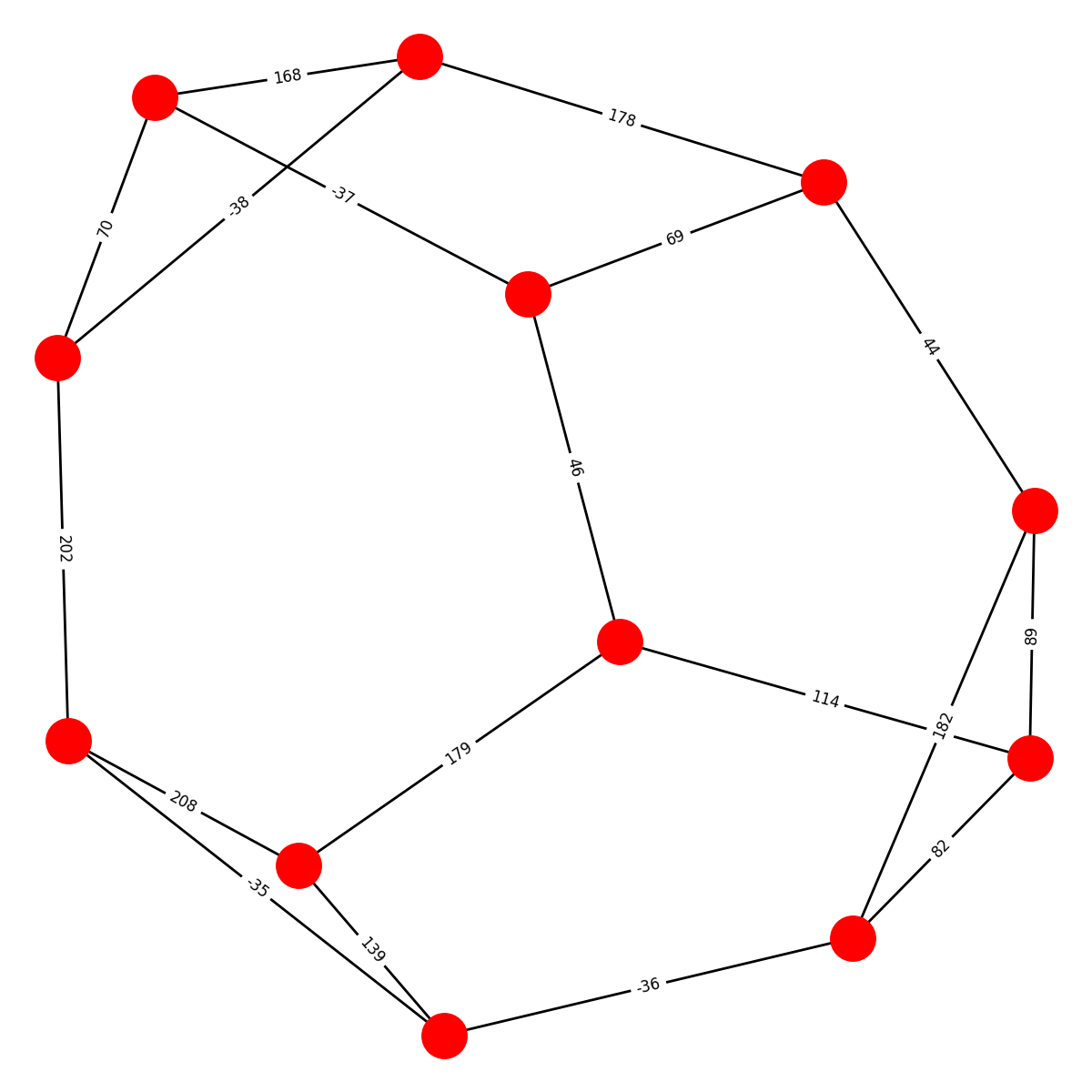
HEAWOOD
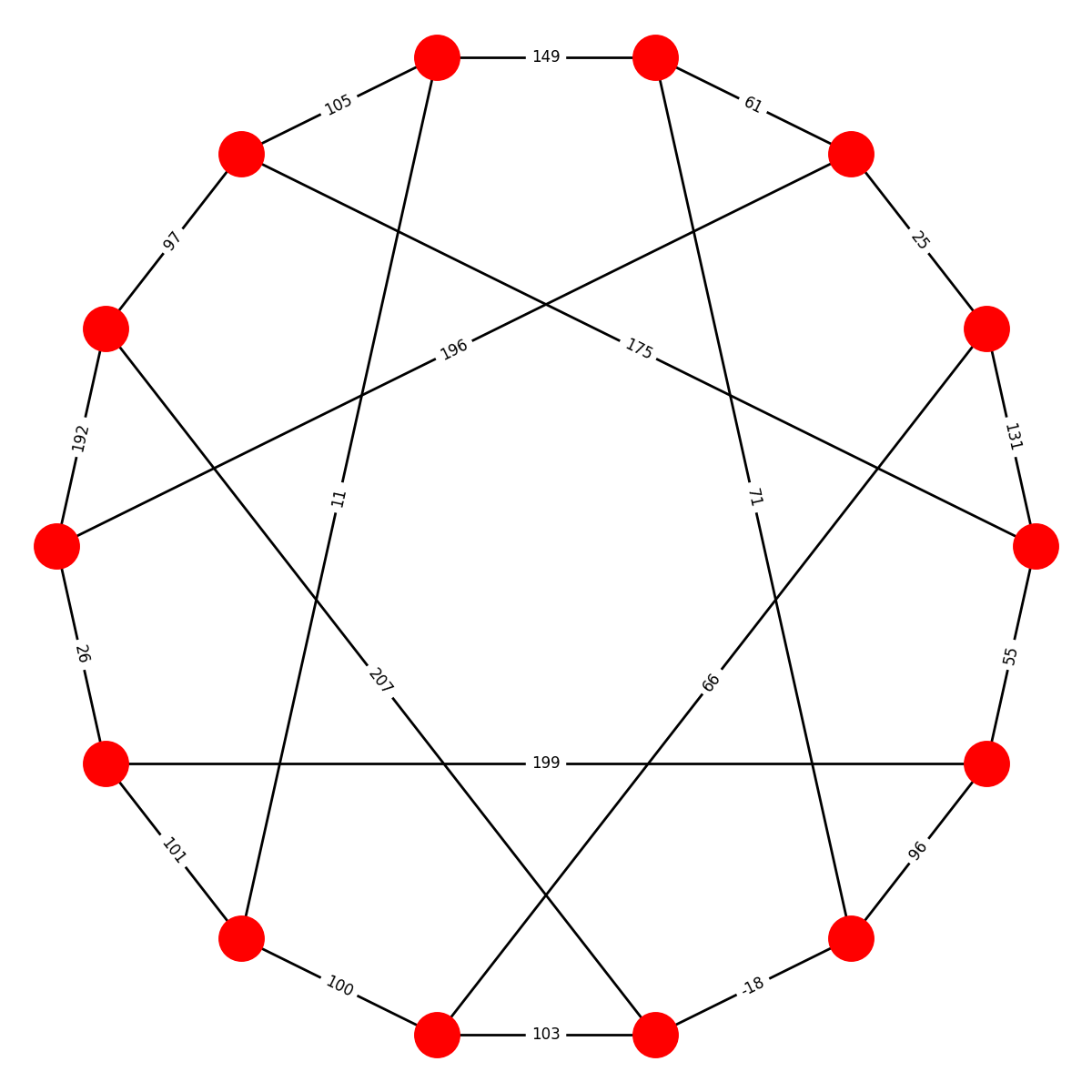
MARKSTROM
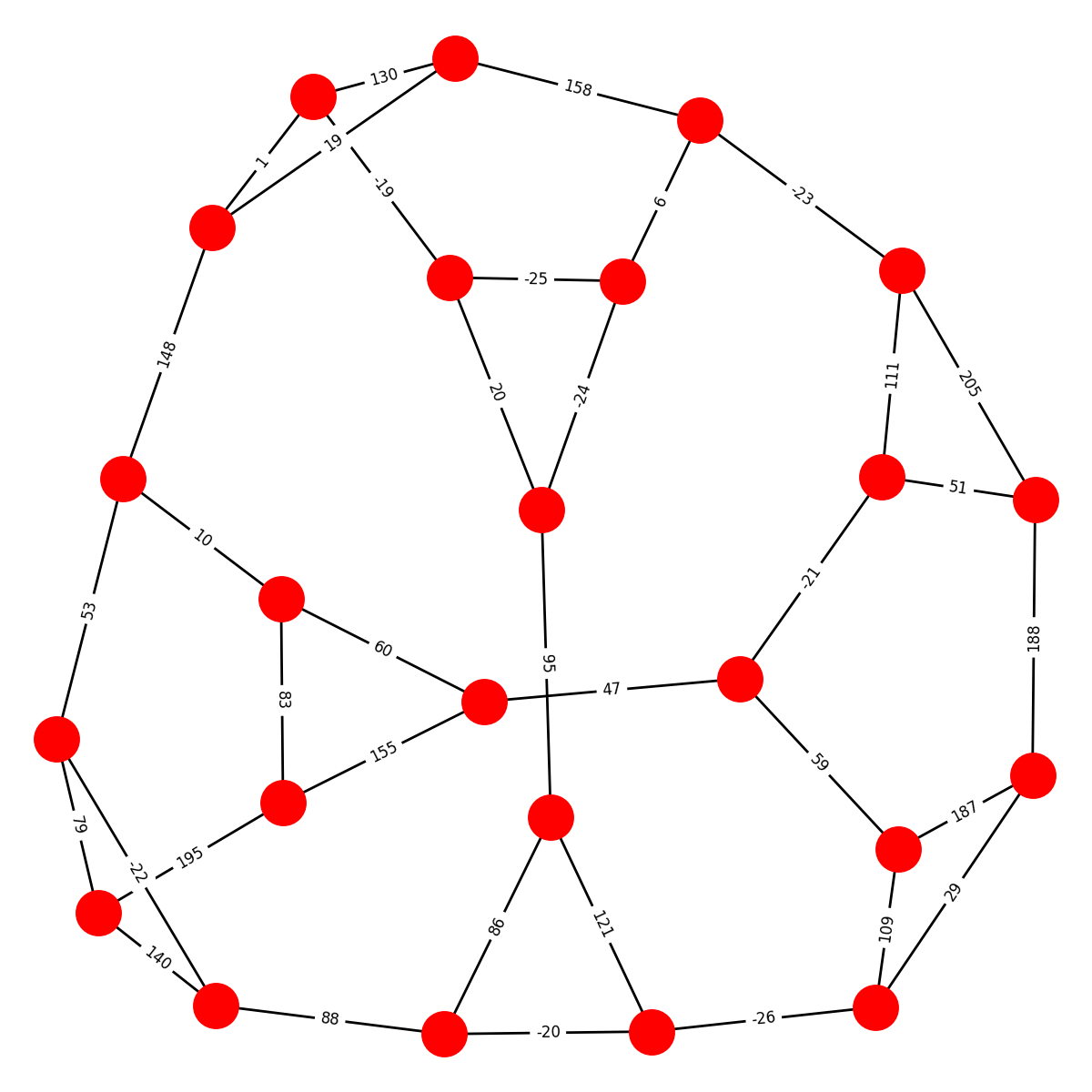
MOBIUS-KANTOR
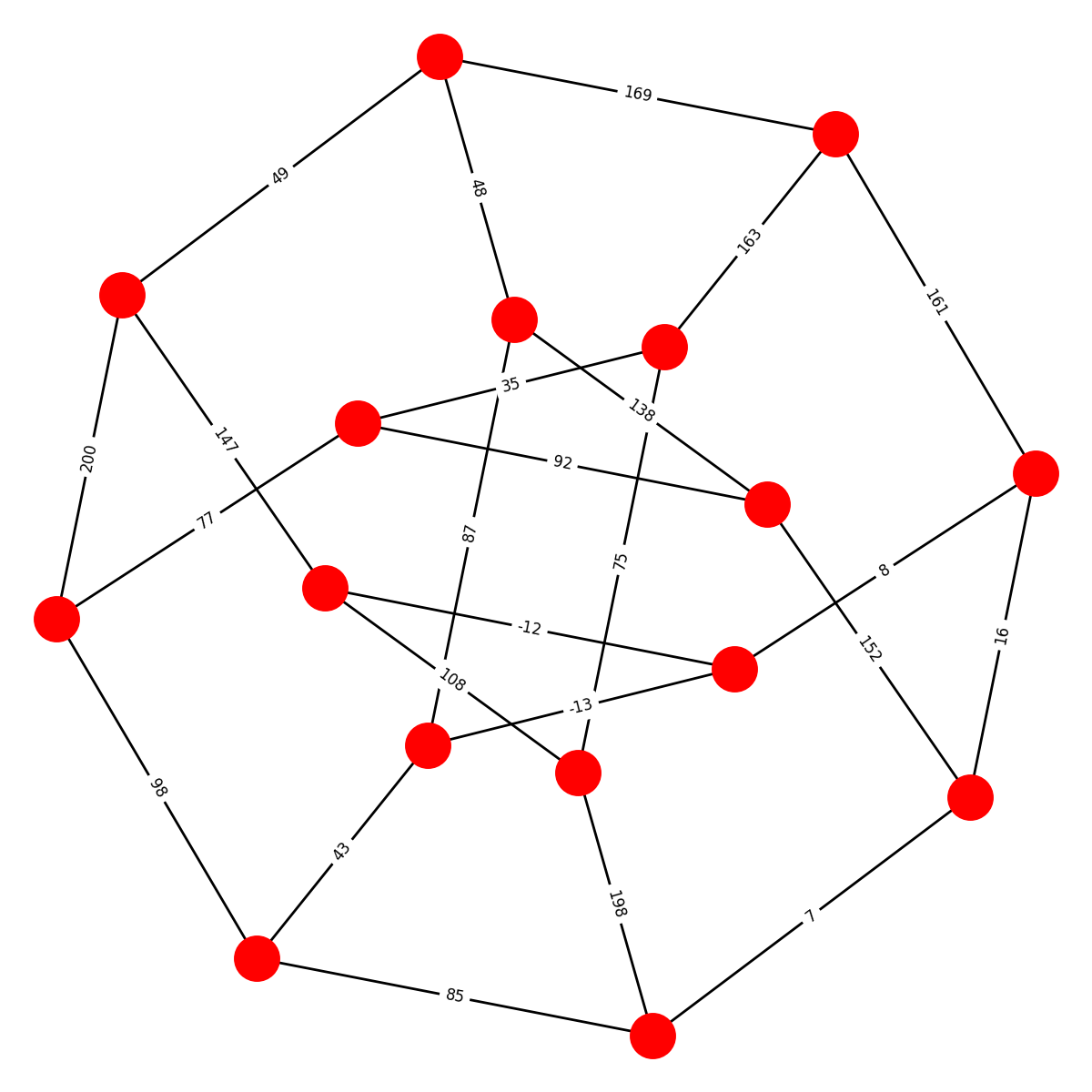
PAPPUS
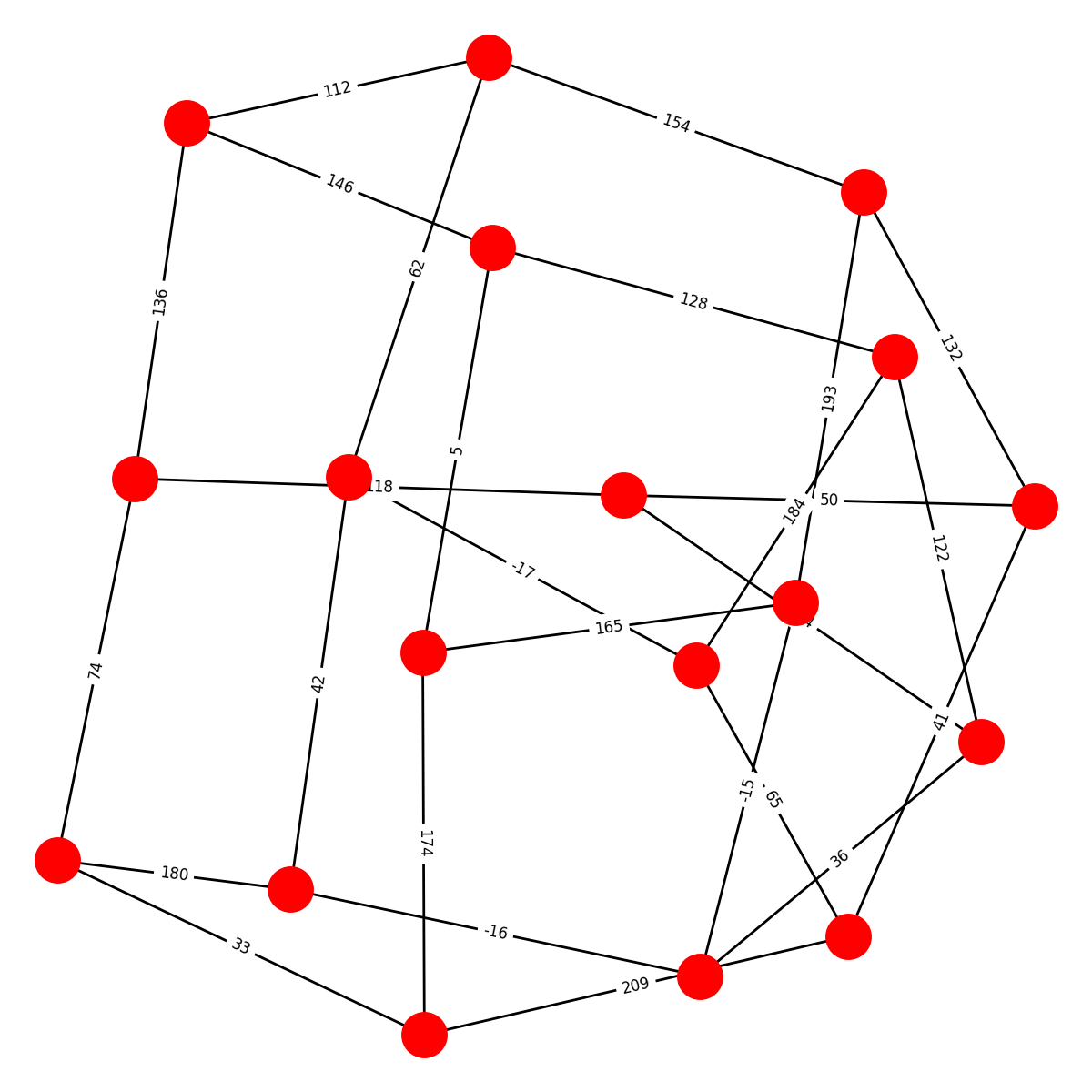
PETERSEN
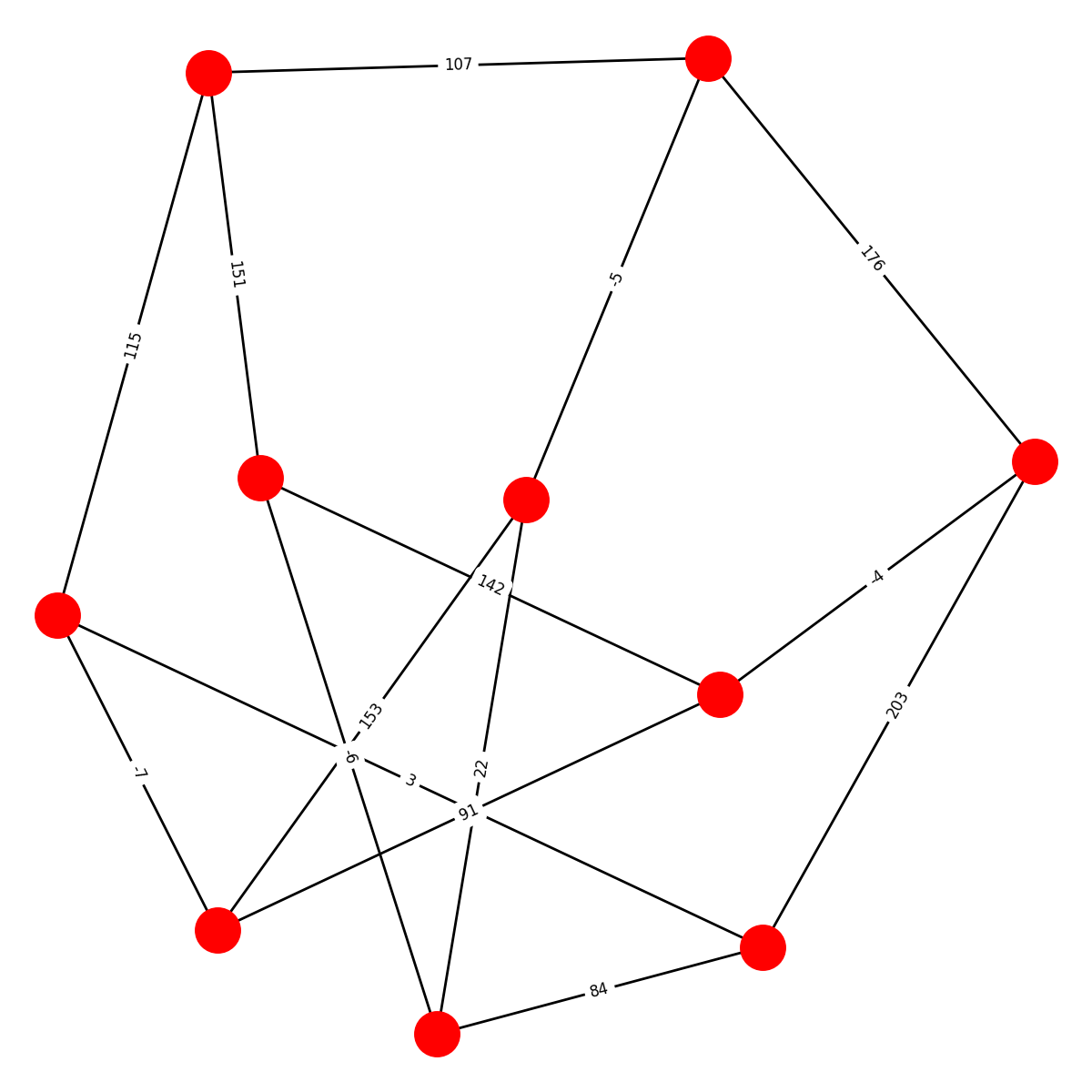
WAGNER
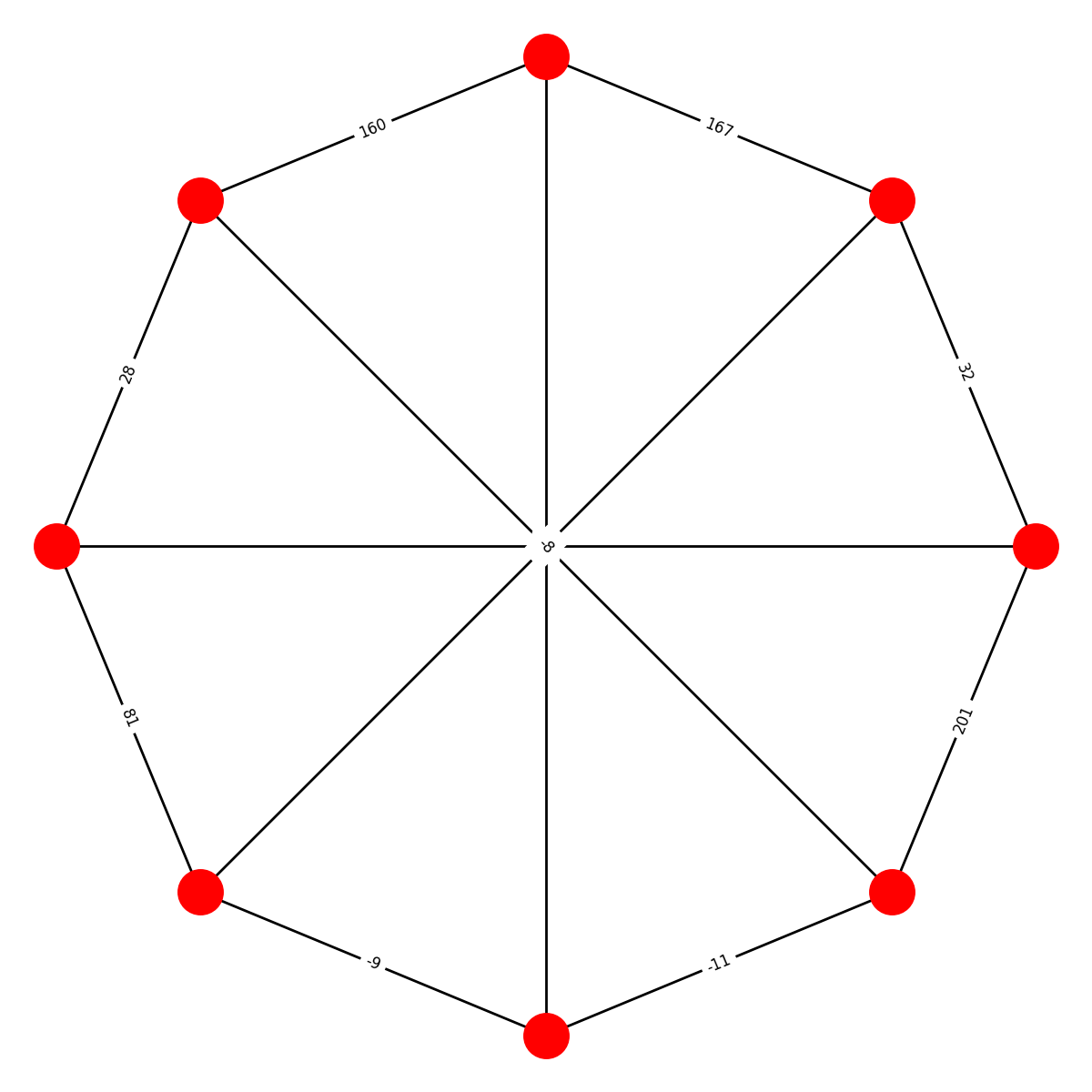
Now what? Solvers need to observe that while the set of positive roots associated with each graph look pretty random, the negative roots are always consecutive integers. Solvers can tally the negative roots used in each graph and order by the range of negative integers. Then solvers can use the count of negative roots as an index into the name of the corresponding graph to extract a letter:
| Order | Graph Name | Negative Roots | # of Negative Roots | Letter |
|---|---|---|---|---|
| 1 | COXETER | -1 to -3 | 3 | X |
| 2 | PETERSEN | -4 to -7 | 4 | E |
| 3 | WAGNER | -8 to -11 | 4 | N |
| 4 | MOBIUS-KANTOR | -12 to -13 | 2 | O |
| 5 | PAPPUS | -14 to -17 | 4 | P |
| 6 | HEAWOOD | -18 | 1 | H |
| 7 | MARKSTROM | -19 to -26 | 8 | O |
| 8 | BIDIAKIS CUBE | -27 | 1 | B |
| 9 | FRANKLIN | -28 to -34 | 7 | I |
| 10 | FRUCHT | -35 to -38 | 4 | C |
This yields the puzzle answer, XENOPHOBIC.
The following table identifies the roots of all of the polynomials, and the graphs to which they belong:
| Graph Name | Roots | Polynomial | ||
|---|---|---|---|---|
| BIDIAKIS CUBE | -27 | 13 | 30 | \(x^3-16x^2-771x+10530\) |
| BIDIAKIS CUBE | -27 | 34 | 197 | \(x^3-204x^2+461x+180846\) |
| BIDIAKIS CUBE | 12 | 14 | 123 | \(x^3-149x^2+3366x-20664\) |
| BIDIAKIS CUBE | 12 | 52 | 157 | \(x^3-221x^2+10672x-97968\) |
| BIDIAKIS CUBE | 13 | 94 | 177 | \(x^3-284x^2+20161x-216294\) |
| BIDIAKIS CUBE | 14 | 58 | 197 | \(x^3-269x^2+14996x-159964\) |
| BIDIAKIS CUBE | 30 | 45 | 76 | \(x^3-151x^2+7050x-102600\) |
| BIDIAKIS CUBE | 34 | 52 | 76 | \(x^3-162x^2+8304x-134368\) |
| BIDIAKIS CUBE | 45 | 134 | 157 | \(x^3-336x^2+34133x-946710\) |
| BIDIAKIS CUBE | 58 | 156 | 177 | \(x^3-391x^2+46926x-1601496\) |
| BIDIAKIS CUBE | 94 | 113 | 134 | \(x^3-341x^2+38360x-1423348\) |
| BIDIAKIS CUBE | 113 | 123 | 156 | \(x^3-392x^2+50715x-2168244\) |
| COXETER | -3 | 23 | 93 | \(x^3-113x^2+1791x+6417\) |
| COXETER | -3 | 56 | 110 | \(x^3-163x^2+5662x+18480\) |
| COXETER | -2 | 73 | 171 | \(x^3-242x^2+11995x+24966\) |
| COXETER | -2 | 119 | 189 | \(x^3-306x^2+21875x+44982\) |
| COXETER | -1 | 4 | 73 | \(x^3-76x^2+215x+292\) |
| COXETER | -1 | 150 | 206 | \(x^3-355x^2+30544x+30900\) |
| COXETER | 2 | 27 | 125 | \(x^3-154x^2+3679x-6750\) |
| COXETER | 2 | 38 | 63 | \(x^3-103x^2+2596x-4788\) |
| COXETER | 4 | 166 | 173 | \(x^3-343x^2+30074x-114872\) |
| COXETER | 18 | 24 | 137 | \(x^3-179x^2+6186x-59184\) |
| COXETER | 18 | 67 | 166 | \(x^3-251x^2+15316x-200196\) |
| COXETER | 23 | 102 | 194 | \(x^3-319x^2+26596x-455124\) |
| COXETER | 24 | 27 | 126 | \(x^3-177x^2+7074x-81648\) |
| COXETER | 38 | 54 | 206 | \(x^3-298x^2+21004x-422712\) |
| COXETER | 39 | 67 | 124 | \(x^3-230x^2+15757x-324012\) |
| COXETER | 39 | 110 | 133 | \(x^3-282x^2+24107x-570570\) |
| COXETER | 54 | 72 | 191 | \(x^3-317x^2+27954x-742608\) |
| COXETER | 56 | 63 | 145 | \(x^3-264x^2+20783x-511560\) |
| COXETER | 72 | 119 | 133 | \(x^3-324x^2+33971x-1139544\) |
| COXETER | 78 | 102 | 117 | \(x^3-297x^2+29016x-930852\) |
| COXETER | 78 | 137 | 191 | \(x^3-406x^2+51751x-2041026\) |
| COXETER | 93 | 126 | 171 | \(x^3-390x^2+49167x-2003778\) |
| COXETER | 106 | 117 | 170 | \(x^3-393x^2+50312x-2108340\) |
| COXETER | 106 | 145 | 173 | \(x^3-424x^2+58793x-2659010\) |
| COXETER | 124 | 144 | 159 | \(x^3-427x^2+60468x-2839104\) |
| COXETER | 125 | 141 | 144 | \(x^3-410x^2+55929x-2538000\) |
| COXETER | 141 | 170 | 189 | \(x^3-500x^2+82749x-4530330\) |
| COXETER | 150 | 159 | 194 | \(x^3-503x^2+83796x-4626900\) |
| FRANKLIN | -34 | -29 | 9 | \(x^3+54x^2+419x-8874\) |
| FRANKLIN | -34 | -28 | 21 | \(x^3+41x^2-350x-19992\) |
| FRANKLIN | -33 | -32 | -28 | \(x^3+93x^2+2876x+29568\) |
| FRANKLIN | -33 | -30 | 90 | \(x^3-27x^2-4680x-89100\) |
| FRANKLIN | -32 | 116 | 185 | \(x^3-269x^2+11828x+686720\) |
| FRANKLIN | -31 | 9 | 127 | \(x^3-105x^2-3073x+35433\) |
| FRANKLIN | -31 | 116 | 186 | \(x^3-271x^2+12214x+668856\) |
| FRANKLIN | -30 | 104 | 185 | \(x^3-259x^2+10570x+577200\) |
| FRANKLIN | -29 | 68 | 104 | \(x^3-143x^2+2084x+205088\) |
| FRANKLIN | 21 | 68 | 183 | \(x^3-272x^2+17715x-261324\) |
| FRANKLIN | 90 | 127 | 172 | \(x^3-389x^2+48754x-1965960\) |
| FRANKLIN | 172 | 183 | 186 | \(x^3-541x^2+97506x-5854536\) |
| FRUCHT | -38 | 70 | 202 | \(x^3-234x^2+3804x+537320\) |
| FRUCHT | -38 | 168 | 178 | \(x^3-308x^2+16756x+1136352\) |
| FRUCHT | -37 | 46 | 69 | \(x^3-78x^2-1081x+117438\) |
| FRUCHT | -37 | 70 | 168 | \(x^3-201x^2+2954x+435120\) |
| FRUCHT | -36 | -35 | 139 | \(x^3-68x^2-8609x-175140\) |
| FRUCHT | -36 | 82 | 182 | \(x^3-228x^2+5420x+537264\) |
| FRUCHT | -35 | 202 | 208 | \(x^3-375x^2+27666x+1470560\) |
| FRUCHT | 44 | 69 | 178 | \(x^3-291x^2+23150x-540408\) |
| FRUCHT | 44 | 89 | 182 | \(x^3-315x^2+28122x-712712\) |
| FRUCHT | 46 | 114 | 179 | \(x^3-339x^2+33884x-938676\) |
| FRUCHT | 82 | 89 | 114 | \(x^3-285x^2+26792x-831972\) |
| FRUCHT | 139 | 179 | 208 | \(x^3-526x^2+91025x-5175248\) |
| HEAWOOD | -18 | 71 | 96 | \(x^3-149x^2+3810x+122688\) |
| HEAWOOD | -18 | 103 | 207 | \(x^3-292x^2+15741x+383778\) |
| HEAWOOD | 11 | 100 | 101 | \(x^3-212x^2+12311x-111100\) |
| HEAWOOD | 11 | 105 | 149 | \(x^3-265x^2+18439x-172095\) |
| HEAWOOD | 25 | 61 | 196 | \(x^3-282x^2+18381x-298900\) |
| HEAWOOD | 25 | 66 | 131 | \(x^3-222x^2+13571x-216150\) |
| HEAWOOD | 26 | 101 | 199 | \(x^3-326x^2+27899x-522574\) |
| HEAWOOD | 26 | 192 | 196 | \(x^3-414x^2+47720x-978432\) |
| HEAWOOD | 55 | 96 | 199 | \(x^3-350x^2+35329x-1050720\) |
| HEAWOOD | 55 | 131 | 175 | \(x^3-361x^2+39755x-1260875\) |
| HEAWOOD | 61 | 71 | 149 | \(x^3-281x^2+23999x-645319\) |
| HEAWOOD | 66 | 100 | 103 | \(x^3-269x^2+23698x-679800\) |
| HEAWOOD | 97 | 105 | 175 | \(x^3-377x^2+45535x-1782375\) |
| HEAWOOD | 97 | 192 | 207 | \(x^3-496x^2+78447x-3855168\) |
| MARKSTROM | -26 | -20 | 121 | \(x^3-75x^2-5046x-62920\) |
| MARKSTROM | -26 | 29 | 109 | \(x^3-112x^2-427x+82186\) |
| MARKSTROM | -25 | -24 | 6 | \(x^3+43x^2+306x-3600\) |
| MARKSTROM | -25 | -19 | 20 | \(x^3+24x^2-405x-9500\) |
| MARKSTROM | -24 | 20 | 95 | \(x^3-91x^2-860x+45600\) |
| MARKSTROM | -23 | 6 | 158 | \(x^3-141x^2-2824x+21804\) |
| MARKSTROM | -23 | 111 | 205 | \(x^3-293x^2+15487x+523365\) |
| MARKSTROM | -22 | 53 | 79 | \(x^3-110x^2+1283x+92114\) |
| MARKSTROM | -22 | 88 | 140 | \(x^3-206x^2+7304x+271040\) |
| MARKSTROM | -21 | 47 | 59 | \(x^3-85x^2+547x+58233\) |
| MARKSTROM | -21 | 51 | 111 | \(x^3-141x^2+2259x+118881\) |
| MARKSTROM | -20 | 86 | 88 | \(x^3-154x^2+4088x+151360\) |
| MARKSTROM | -19 | 1 | 130 | \(x^3-112x^2-2359x+2470\) |
| MARKSTROM | 1 | 19 | 148 | \(x^3-168x^2+2979x-2812\) |
| MARKSTROM | 10 | 53 | 148 | \(x^3-211x^2+9854x-78440\) |
| MARKSTROM | 10 | 60 | 83 | \(x^3-153x^2+6410x-49800\) |
| MARKSTROM | 19 | 130 | 158 | \(x^3-307x^2+26012x-390260\) |
| MARKSTROM | 29 | 187 | 188 | \(x^3-404x^2+46031x-1019524\) |
| MARKSTROM | 47 | 60 | 155 | \(x^3-262x^2+19405x-437100\) |
| MARKSTROM | 51 | 188 | 205 | \(x^3-444x^2+58583x-1965540\) |
| MARKSTROM | 59 | 109 | 187 | \(x^3-355x^2+37847x-1202597\) |
| MARKSTROM | 79 | 140 | 195 | \(x^3-414x^2+53765x-2156700\) |
| MARKSTROM | 83 | 155 | 195 | \(x^3-433x^2+59275x-2508675\) |
| MARKSTROM | 86 | 95 | 121 | \(x^3-302x^2+30071x-988570\) |
| MOBIUS-KANTOR | -13 | -12 | 8 | \(x^3+17x^2-44x-1248\) |
| MOBIUS-KANTOR | -13 | 43 | 87 | \(x^3-117x^2+2051x+48633\) |
| MOBIUS-KANTOR | -12 | 108 | 147 | \(x^3-243x^2+12816x+190512\) |
| MOBIUS-KANTOR | 7 | 16 | 152 | \(x^3-175x^2+3608x-17024\) |
| MOBIUS-KANTOR | 7 | 85 | 198 | \(x^3-290x^2+18811x-117810\) |
| MOBIUS-KANTOR | 8 | 16 | 161 | \(x^3-185x^2+3992x-20608\) |
| MOBIUS-KANTOR | 35 | 75 | 163 | \(x^3-273x^2+20555x-427875\) |
| MOBIUS-KANTOR | 35 | 77 | 92 | \(x^3-204x^2+12999x-247940\) |
| MOBIUS-KANTOR | 43 | 85 | 98 | \(x^3-226x^2+16199x-358190\) |
| MOBIUS-KANTOR | 48 | 49 | 169 | \(x^3-266x^2+18745x-397488\) |
| MOBIUS-KANTOR | 48 | 87 | 138 | \(x^3-273x^2+22806x-576288\) |
| MOBIUS-KANTOR | 49 | 147 | 200 | \(x^3-396x^2+46403x-1440600\) |
| MOBIUS-KANTOR | 75 | 108 | 198 | \(x^3-381x^2+44334x-1603800\) |
| MOBIUS-KANTOR | 77 | 98 | 200 | \(x^3-375x^2+42546x-1509200\) |
| MOBIUS-KANTOR | 92 | 138 | 152 | \(x^3-382x^2+47656x-1929792\) |
| MOBIUS-KANTOR | 161 | 163 | 169 | \(x^3-493x^2+80999x-4435067\) |
| PAPPUS | -17 | 42 | 62 | \(x^3-87x^2+836x+44268\) |
| PAPPUS | -17 | 65 | 184 | \(x^3-232x^2+7727x+203320\) |
| PAPPUS | -16 | -15 | 36 | \(x^3-5x^2-876x-8640\) |
| PAPPUS | -16 | 42 | 180 | \(x^3-206x^2+4008x+120960\) |
| PAPPUS | -15 | 165 | 193 | \(x^3-343x^2+26475x+477675\) |
| PAPPUS | -14 | 36 | 122 | \(x^3-144x^2+2180x+61488\) |
| PAPPUS | -14 | 50 | 118 | \(x^3-154x^2+3548x+82600\) |
| PAPPUS | 5 | 128 | 146 | \(x^3-279x^2+20058x-93440\) |
| PAPPUS | 5 | 165 | 174 | \(x^3-344x^2+30405x-143550\) |
| PAPPUS | 33 | 74 | 180 | \(x^3-287x^2+21702x-439560\) |
| PAPPUS | 33 | 174 | 209 | \(x^3-416x^2+49005x-1200078\) |
| PAPPUS | 41 | 50 | 132 | \(x^3-223x^2+14062x-270600\) |
| PAPPUS | 41 | 65 | 209 | \(x^3-315x^2+24819x-556985\) |
| PAPPUS | 62 | 112 | 154 | \(x^3-328x^2+33740x-1069376\) |
| PAPPUS | 74 | 118 | 136 | \(x^3-328x^2+34844x-1187552\) |
| PAPPUS | 112 | 136 | 146 | \(x^3-394x^2+51440x-2223872\) |
| PAPPUS | 122 | 128 | 184 | \(x^3-434x^2+61616x-2873344\) |
| PAPPUS | 132 | 154 | 193 | \(x^3-479x^2+75526x-3923304\) |
| PETERSEN | -7 | 3 | 115 | \(x^3-111x^2-481x+2415\) |
| PETERSEN | -7 | 91 | 153 | \(x^3-237x^2+12215x+97461\) |
| PETERSEN | -6 | 22 | 84 | \(x^3-100x^2+1212x+11088\) |
| PETERSEN | -6 | 142 | 151 | \(x^3-287x^2+19684x+128652\) |
| PETERSEN | -5 | 22 | 153 | \(x^3-170x^2+2491x+16830\) |
| PETERSEN | -5 | 107 | 176 | \(x^3-278x^2+17417x+94160\) |
| PETERSEN | -4 | 91 | 142 | \(x^3-229x^2+11990x+51688\) |
| PETERSEN | -4 | 176 | 203 | \(x^3-375x^2+34212x+142912\) |
| PETERSEN | 3 | 84 | 203 | \(x^3-290x^2+17913x-51156\) |
| PETERSEN | 107 | 115 | 151 | \(x^3-373x^2+45827x-1858055\) |
| WAGNER | -11 | -10 | -9 | \(x^3+30x^2+299x+990\) |
| WAGNER | -11 | -8 | 201 | \(x^3-182x^2-3731x-17688\) |
| WAGNER | -10 | 160 | 167 | \(x^3-317x^2+23450x+267200\) |
| WAGNER | -9 | 81 | 204 | \(x^3-276x^2+13959x+148716\) |
| WAGNER | -8 | 28 | 160 | \(x^3-180x^2+2976x+35840\) |
| WAGNER | 28 | 40 | 81 | \(x^3-149x^2+6628x-90720\) |
| WAGNER | 32 | 40 | 201 | \(x^3-273x^2+15752x-257280\) |
| WAGNER | 32 | 167 | 204 | \(x^3-403x^2+45940x-1090176\) |