Back to Dmytro Taranovsky's home page
View as Microsoft Word document

Dmytro Taranovsky

Date Started: March 16, 2001

Last Modified: May 21, 2001

Applications of General Relativity

This paper continues the discussion on the structure of general relativity and presents the most relevant applications such as gravitational waves. The paper does not cover all applications, and does not cover electromagnetism. Its style is informal. Reading it requires understanding of General Relativity by Dmytro Taranovsky or an equivalent.

Section 1: Additional Basic Concepts

The choice of 8π in

G=8πT

defines what is meant by mass of amount 1. It is selected so that the gravitational constant is equal 1. For fast unit conversion, you may want to note that 1=G/c²≈7.425*10^-28 m/kg.

(Meter is abbreviated 'm', kilogram--'kg', second--'s').

Some physicists believe that space has an inherent stress energy tensor: Λg, where Λ is cosmological constant. Λ is very close to 0. Cosmological constant is important primarily for the second derivative of the size of the universe.

A generalized Lorentz transformation is transformation under which if g=η before the transformation, then g=η after the transformation. It can be viewed as a rotation in space-time.

Contravariant derivatives are written like covariant except that they appear as superscripts rather than subscripts; they are obtained through raising the index in the contravariant derivative:

a^,u≡g^uv*a_,v.

Metric is often represented as space-time interval in terms of the coordinate changes. For example, in

ds²=‑dt²+dx²+dy²+dz²,

ds² represents the metric for the locally normal frame of reference. Note: When coordinates are distinguished by name rather than index, superscripts are in most cases interpreted as powers.

Two manifolds are called physically equivalent if a one-to-one transformation exists between the manifolds that preserves continuity and metric. Geometry of space-time is whether space-time is physically equivalent to a particular manifold.

Symbol '<<' means in many times smaller. In daily life, most velocities are <<1≈3*10⁸m/s. That is why speed is often expressed in terms of m/s as opposed to a real number.

4-dimensional Laplacian is defined by the equation

⃞f≡f_,u^,u.

(Symbol ∇² is usually used instead of ⃞; however, in a locally inertial frame of reference, ∇² is sometimes used as ∂²/∂(x¹)²+∂²/∂(x²)²+∂²/∂(x³)²).

For a non-interacting particle, rest mass is conserved.

A trajectory is called:

time-like if ||u||<0,

light-like if u is undefined and

space-like if ||u||>0.

No time-like or light-like trajectories are closed--no travel back in time. Lack of closure allows defining time: a continuous function T (event→real number) that if A causes B, then T(A)<T(B). (If travel back in time would be possible, then the following object could be set up: The object receives signal 0 or 1 and sends itself (back in time) the opposite signal: If the object receives 0, it sends 1, and thus receives 1--a contradiction; if it receives 1, it sends 0, and receives 0--a contradiction. Since such object is contradictory, it does not exist, and travel back in time is impossible.) All objects of nonzero rest mass follow time-like trajectories. All objects of zero rest mass (light has zero rest mass) follow light-like trajectories.

Section 2: Linearization and Newtonian Approximation

A coordinate system is called nearly Lorentz if

g=η+h where h_ab<<η_ab.

h_ab transforms like a tensor of rank (0, 2) in a generalized Lorentz transformation. Solar system can be described accurately by a nearly Lorentz coordinate system. For a nearly Lorentz coordinate system,

R_abuv ≈½*(h_av,bu + h_bu,av - h_au,bv - h_bv,au).

h^u_b ≡ η_ua* h_ab; h^uv ≡ η^vb * h^u_b;

. (Schutz 204)

Coordinates can always be selected to adhere to the Lorenz gauge condition:

(do not forget the summation). The linear approximation to Einstein field equation is

⃞=-16πT (Schutz 205)

in such coordinates. The equation, being linear in terms of the metric, is more computationally friendly then the exact equation. Its use requires almost Cartesian coordinates system and thus absence of strong gravity.

When velocities are <<1 (such as one thousand kilometers per second), ⁰⁰ is the dominant term of and mass density (which is approximately rest mass density),

ρ=T⁰⁰,

is the dominant part of the stress-energy tensor.

⃞=(-∂²/∂t²+∇²).

∂/∂t=∂/∂xⁱ*∂xⁱ/∂t= v∇.

Since v<<1, -∂²/∂t²=v²∇² can be ignored. Thus,

∇²⁰⁰=-16πρ. (Schutz 206)

Gravitational potential (a real number),

φ≡-⁰⁰/4.

Thus, the non-relativistic equation for gravity is

∇²φ=4πρ.

Through substitution, the metric can be shown to be

ds²=-(1+2φ)dt²+(1-2φ)(dx²+dy²+dz²). (Schutz 206)

For a spherically symmetric object with radius R<r,

φ=-M/r.

Thus, by linearity, for a continuous mass distribution,

.

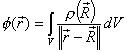Non-interacting particles move so that

dpⁱ/dt= ‑p⁴∂φ/∂xⁱ

(the equation does not assume that 3-velocity is small) where p is 4-momentum.

Section 3: Metric for static spherically symmetric cases

In such cases, the field equation can often be solved exactly. The cases occur in non-rotating stars, heavy compact objects (such as white dwarfs and neutron stars), and black holes. The coordinates chosen are usually t (time), r (radius, whose value is derived from the formula for area of the sphere), and Ω (that covers the two angle coordinates on a sphere: dΩ²=dθ²+sin²θ dφ²). Then, the metric is

ds²=-f(r)dt²+g(r)dr²+ r²dΩ². (Schutz 254)

If the entire mass (M) is at the origin,

f(R)=(1-2M/R) and

g(R)=1/(1-2M/R). (Schutz 258)

If R<2M (f(R)<0 and g(r)<0), then all objects (including light) must move inward. Such objects are soon destroyed; all that remains for external observation is total mass, total electric charge, and total angular momentum. Such object is called a black hole. A black hole (whose mass is millions of times larger than that of the sun) is located in the center of most galaxies including Milky Way (the galaxy in which Earth resides).

Section 4: Gravitational Waves

The field equation allows wavelike solutions in empty space. Since gravitational waves have not been detected (as of 2001), the waves passing through the Earth are very weak. Weakness of gravitational waves allows linear approximation. Gravitational waves are created through acceleration of heavy objects, such as when two stars rotate around each other at a small distance.

In free space, the linearized equation (⃞=-16πT) has a general solution that is (an infinite but converging) sum of plane waves. For best examination of gravitational waves, a nearly Lorentz frame of reference satisfying Lorenz gauge condition and h^a_a=0 is used. A plane wave has

,

where g^abk_ak_b=0.

Note: g^abk_ak_b=||k||=(k₁)²+(k₂)²+(k₃)²-(k₄)².

Its phase is φ, angular frequency--k₄, frequency--k₄/(2π), and its wavelength:

λ=sqrt((k₁)²+(k₂)²+(k₃)²),

which is equal its frequency.

For , let x, y, and z be coordinates of space such that the wave travels in z direction. Then,

A_xx=-A_yy, A_xy=A_yx, (Schutz 217)

and other components are zero. (Note: Here coordinate names rather than indexes identify the components.)

Using the coordinate system selected, gravitational waves do not change locations of non-interacting objects at rest. Instead, they distort distance between objects through change in the metric. (Distance squared for locations that are not far apart and that are separated by (∆x, ∆y, ∆z) is (∆x)²+(∆y)²+(∆z)²+h_xx∆x∆x+ h_yy∆y∆y+ h_zz∆x∆x+ 2h_xy∆x∆y+2h_xz∆x∆z+2h_yz∆y∆z). Note that gravitational waves do not affect interval in time in the chosen coordinate system.

By selectively choosing x and y coordinates, A_xy can be made to equal 0. The relative value of A_xx and A_xy is called polarization of the wave. Polarization states whether the oscillation is along the coordinate axes or the diagonals.

Gravitational waves can be detected by measuring oscillations in proper distance (based on the metric) of objects. They can also be measured by holding proper distance fixed (by, say, using a rod) and measuring the forces--to maintain fixed proper distance, objects have to accelerate.

Since gravitational waves cause force, they carry energy. Energy flux per unit of area of a plane gravitational plane wave is (in the direction of propagation)

F=Ω²<h_uvh^uv>/(32π), (Schutz 238)

Where Ω is frequency, and '<...>' indicates average over time.

Radiation of energy through gravitational waves causes binary stars to increase period of revolution through decreased distance. Such increase in period was detected.

Section 5: Additional Applications

Item 1: Gravitational Red shift.

In approximation in which gravitational potential is defined, light frequency changes approximately according to

υ′=(φ-φ′+1)υ,

that is as light escapes from gravity, its frequency decreases. Its energy is proportional to frequency. The frequency is also dependent on the coordinate system:

υ′=sqrt((1+v)/(1-v))υ,

where υ is frequency in the initial coordinate system, υ′ is frequency in the new coordinate system, and v is the component of 3-velocity of the new coordinate system towards the old. Historically, one of the confirmations of general relativity was that light of heavy stars had lower frequency than predicted from the dynamics of the stars.

Item 2: Cosmology:

Cosmology is the theory about the development of the universe as a whole, and it is based on solving Einstein Field Equation for the entire universe with certain simplistic assumptions. Combined with observational data, the solutions tell that as time increase, the size of the universe increases; the universe has a finite size in space; and at certain time (12-15 billion years ago) the space was only one point. Like other models, cosmology is relevant not because it suggests the past, but because it allows for better analysis of the data about the present and because it suggests the future.

According to observations, on the scale comparable to the size of the universe, matter is homogenous and isotropic (no preferred direction or position). The metric is approximately,

ds²=-dt²+R²(t)*(dr²/(1-k*r²)+r²dΩ²), (Schutz 324)

where R(t) is size of universe at time t and where k depends only on time.

Unfortunately, much of the cosmology is uncertain, so the information in this item is subject to change.

Item 3: Miscellaneous Applications

Frame dragging: When a body rotates, incoming objects are pressured to rotate with the body, even if the incoming objects are in vacuum.

General Positioning System (GPS) consists of satellites that send electromagnetic signals. The signals arrive with delay because speed of light is 1, not infinity. The delay allows the receiver to calculate its location up to 10meters. General theory of relativity is needed in these calculations.

Galaxies sometimes act as gravitational lenses for faraway objects. (Because of non-Euclidean geometry due to galaxies, angular size and intensity of the object as viewed from Earth can be increased because of the galaxy.)

As predicted by classical gravity, a planet rotates around a star in an ellipse. As general relativity shows, however, the axis of the ellipse slowly rotates.

Section 6: Preface to Quantum Mechanics

Much of the universe is described in terms of tensor fields. Can these fields be split up into independent elements indefinitively? As was discovered in the 20^th century, no: All fields are quantized. The quantization is essential for the structure of the universe. It is described by quantum field theory and the standard model (to be covered in a later paper).

Section 7: Exercises

Please note: The exercises have not been tested for difficulty to the readers, and are not sufficient for some readers.

1. Fill in the missing steps in derivation of

ds²=-(1+2φ)dt²+(1-2φ)(dx²+dy²+dz²).

.
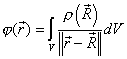2. The coordinate system used for black holes does not work when R=2M. Find and justify a coordinate system that covers the surface R=2M as well. (Note: If you cannot solve this difficult problem, you can find such a coordinate system in Schutz (292).)
3. For the black holes, prove that no coordinate system can include a point at R=0. Thus, R=0 is not part of the manifold--it is a singularity.

4. a) Show that a plane wave is a solution of the linear field equation for free space (⃞=0).
b) Show that polarization so that A_xy=0 can be obtained through rotation along z-axis.

Section 8: Readings about General Relativity

Introduction to Tensor Calculus and Continuum Mechanics by Heinbockel provides an excellent introduction to the mathematical background: conventions, definition of tensors, tensor operations, metric, covariant differentiation, Riemann Christoffel tensor, and other topics.

A First Course in General Relativity provides a good introduction to general relativity. Almost half of the book develops needed mathematical background. Applications--gravitational waves, stars, black holes, and cosmology--are included. The book is easy to read (but still requires careful studying and solving problems).

The author used the following sources in learning general relativity:

Baez, John. General Relativity Tutorial. 1996-1997. Online. Internet. Accessed: February 7,

2001. Available: http://mat.ucr.edu/home/baez/gr/gr.html.

Dunsby, Peter. Tensors and Relativity. 1996-2000. Online. Internet. Accessed: February 22,

2001. Available: http://vishnu.mth.uct.ac.za/omei/gr.

Heinbockel, John H. Introduction to Tensor Calculus and Continuum Mechanics. 1997.

Online. Internet. Accessed: February 12, 2001. Available:

http://www.math.odu.edu/~jhh/counter2.html.

Misner, Charles W., Thorne, Kip S., Wheeler, John Archibald. Gravitation. W. H. Freeman and

Company: San Francisco, 1973.

Schutz, Bernand F. A First Course in General Relativity. Cambridge University Press:

Cambridge MA, 1986.

Waner, Stefan. Introduction to Differential Geometry and General Relativity. 1998. Online.

Internet. Accessed: February 27, 2001. Available:

http://147.4.150.5/~matscw/diff_geom/tc.html.

Acknowledgement: Jay Fogleman spent several hours with me to help me understand the theory and to make my paper easy to read.

Notation specifications: Comma (not semicolon) is used for contravariant derivatives. Metric is selected so that ||U||=-1.