Back to Dmytro Taranovsky's home page
View as Microsoft Word document
Dmytro Taranovsky
Date Started: February 12, 2001
Last Modified: January 4, 2002
General Relativity
The paper presents non-quantum physics with emphasis on the general theory of relativity. The entire theory but not many applications or approximation techniques are included. Required mathematics is rigorously developed.
Part I: Mathematical Background
Section 1: Special Mathematical Notation
To keep formulas simple, special notation is used. When a statement has free indexes (superscripts and subscripts that are variable and not assigned a particular value), the statement is assumed true for all values of the indexes. For example, "xi=cit where i can be 1, 2, or 3" means "x1=c1t, x2=c2t, and x3=c3t". Because of the extensive need for indexes, superscripts of variables are typically interpreted as indexes instead of powers. Instead, use parenthesis to express power. For example, x2≠x*x=(x)2. Sequences are denoted as follows: x1, x2, ..., xn is x1, x2, ..., xn‑1, xn if n>1, is x1 if n=1, and is nothing when n=0.
Summation
convention states that when an index variable appears twice in an
expression, summation over the allowed values of the index is assumed. For
example, the chain rule simplifies to![]() . To avoid using the summation
convention, state "no summation" or enclose the indexes in parenthesis. The
expression must be expanded before applying the summation: (xi+yi)*(xi+yi)=xixi+2xiyi+yiyi=(x1+y1)2+(x2+y2)2
with i=1, 2. The summation is not assumed when the indexes (after the
expression is expanded) are separated by addition or subtraction: ai+bi
is not summed up over all i. The summation occurs as close to the
indexes as reasonable: (xiyi)2
with i=1, 2 is (x1y1+x2y2)2.
When manipulating expressions using the summation convention, you can usually ignore
implicit summation sign.
. To avoid using the summation
convention, state "no summation" or enclose the indexes in parenthesis. The
expression must be expanded before applying the summation: (xi+yi)*(xi+yi)=xixi+2xiyi+yiyi=(x1+y1)2+(x2+y2)2
with i=1, 2. The summation is not assumed when the indexes (after the
expression is expanded) are separated by addition or subtraction: ai+bi
is not summed up over all i. The summation occurs as close to the
indexes as reasonable: (xiyi)2
with i=1, 2 is (x1y1+x2y2)2.
When manipulating expressions using the summation convention, you can usually ignore
implicit summation sign.
Section 2: Tensors and Tensor Operations
A tensor T is defined as
an ordered collection of its components: ![]() where each of the i and each of
the j can assume any integer value from 1 to N and all
components are real numbers. N is called dimension, m is
contravariant order, n is covariant order, and (m, n) is rank of T.
(The total number of components is Nm+n.) Tensor field
assigns a tensor to every point in a space. Tensors are often referred by
their components.
where each of the i and each of
the j can assume any integer value from 1 to N and all
components are real numbers. N is called dimension, m is
contravariant order, n is covariant order, and (m, n) is rank of T.
(The total number of components is Nm+n.) Tensor field
assigns a tensor to every point in a space. Tensors are often referred by
their components.
Definition: Let T be the
value of a tensor field at a certain point. Let T have components ![]() in
coordinates x1, x2, ..., xN. Then in the
coordinates
in
coordinates x1, x2, ..., xN. Then in the
coordinates ![]() the
components of T are
the
components of T are 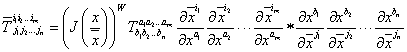 where W is a real number
(often a fraction or an integer) that is dependent only on the tensor field.
(Do not forget to use the summation convention on every a and every b.)
If W=0, the tensor is said to be absolute, otherwise the tensor is a
relative tensor of weight W. Unless stated otherwise, W=0.
where W is a real number
(often a fraction or an integer) that is dependent only on the tensor field.
(Do not forget to use the summation convention on every a and every b.)
If W=0, the tensor is said to be absolute, otherwise the tensor is a
relative tensor of weight W. Unless stated otherwise, W=0.
Theorem: The definition is non-contradictory for arbitrary tensor fields and coordinates provided that the expression is defined and the Jacobian is not zero.
Tensors are added, multiplied by a scalar, and subtracted
component by component: C=A+B means![]() ; B=c*A means
; B=c*A means![]() ; -B=-1*B; A-B=A+-B.
The operations above are undefined if there is a mismatch in rank or
dimension. Outer product, C=A⊗B, means
; -B=-1*B; A-B=A+-B.
The operations above are undefined if there is a mismatch in rank or
dimension. Outer product, C=A⊗B, means![]() . Contraction is
setting a subscript equal to a superscript and invoking the summation
convention. For example,
. Contraction is
setting a subscript equal to a superscript and invoking the summation
convention. For example, ![]() . (The covariant and contravariant
orders are decreased by 1.) Inner product is an outer product followed
by contraction(s). Addition, subtraction, multiplication by a scalar,
contraction, outer product, and thus inner product of tensors can be shown to
transform under coordinate change as tensors would by the definition. For example,
C=A⊗B⇔
. (The covariant and contravariant
orders are decreased by 1.) Inner product is an outer product followed
by contraction(s). Addition, subtraction, multiplication by a scalar,
contraction, outer product, and thus inner product of tensors can be shown to
transform under coordinate change as tensors would by the definition. For example,
C=A⊗B⇔![]() where the bars indicate a
new coordinate system. Tensor differentiation and integration, if done
component by component, does not transform properly: often,
where the bars indicate a
new coordinate system. Tensor differentiation and integration, if done
component by component, does not transform properly: often, ![]() . Section 6
describes how to differentiate tensors.
. Section 6
describes how to differentiate tensors.
When a quantity with proper components is defined in multiple coordinate systems or in terms of tensors, the quantity is said to be a tensor if it always obeys the transformation equation. Tensors are usually preferred over "nontensors" because a tensor needs to be defined in only one coordinate system and because change of tensor components under coordinate transformations is predictable and depend only on the coordinates and the nature of the tensor.
Section 3: Examples of Tensors
Kronecker
delta, also called identity tensor, δij=δij=δij=1
if i=j and 0 otherwise. Generalized delta tensor has components![]() . Each component
is 0 if ai=aj or bi=bj
for some unequal i and j. Otherwise, if a1a2...an
is an even permutation of b1b2...bn, the
component is one, odd permutation--the component is -1. Otherwise (that is if ∃i (1≤i≤n) ∀j
(1≤j≤n) aj≠bi), the
component is zero. T is called is symmetric with respect to ix
and iy (x≠y)
if exchange of values of ix and iy does not
affect any of the components, and anti-symmetric if the exchange
multiplies every component by -1. (Both ix and iy
must be either subscripts or superscripts.) For example, δij
is a symmetric tensor;
. Each component
is 0 if ai=aj or bi=bj
for some unequal i and j. Otherwise, if a1a2...an
is an even permutation of b1b2...bn, the
component is one, odd permutation--the component is -1. Otherwise (that is if ∃i (1≤i≤n) ∀j
(1≤j≤n) aj≠bi), the
component is zero. T is called is symmetric with respect to ix
and iy (x≠y)
if exchange of values of ix and iy does not
affect any of the components, and anti-symmetric if the exchange
multiplies every component by -1. (Both ix and iy
must be either subscripts or superscripts.) For example, δij
is a symmetric tensor; ![]() is an anti-symmetric tensor with respect
to any subscripts or superscripts. Note that if T is anti-symmetric with
respect to ix and iy, then the value of
every component where ix=iy is zero. Permutation
tensor, e, is anti-symmetric with respect to any two components, and
e12..n=e12..n=1. Weight of eij..k,
eij..k, δij, and δij
is not zero.
is an anti-symmetric tensor with respect
to any subscripts or superscripts. Note that if T is anti-symmetric with
respect to ix and iy, then the value of
every component where ix=iy is zero. Permutation
tensor, e, is anti-symmetric with respect to any two components, and
e12..n=e12..n=1. Weight of eij..k,
eij..k, δij, and δij
is not zero.
A tensor of rank (0, 0) is called a scalar and has only one component. A tensor of rank (1, 0) is called contravariant vector or simply vector. For example, position and velocity are vectors. A contravariant vector can be displayed as a sequence such as (a1, a2, ..., an). The transformation equation implies that in smaller coordinates vector components are larger. A tensor of rank (0, 1) is called covariant vector or a 1-form. Covariant vectors can be interpreted as assigning for each contravariant vector a real number in a linear way through a dot product. The transformation equation implies that larger coordinates cause larger components.
Let EiEj...EkElEm...En
be defined such that (EiEj...EkElEm...En)![]() =1 and other
components are zero. EiEj...EkElEm...En
form a basis since an arbitrary tensor A=
=1 and other
components are zero. EiEj...EkElEm...En
form a basis since an arbitrary tensor A=![]() EiEj...EkElEm...En (The summation is over all components.)
(Visualization of 1-forms: xiEi as a set of yiEi
such that xiyi=1.)
EiEj...EkElEm...En (The summation is over all components.)
(Visualization of 1-forms: xiEi as a set of yiEi
such that xiyi=1.)
A multilinear form is a function that takes n vectors and returns a scalar in a linear way with respect to each of the vectors. For example, f(cE1, E2) = cf(E1, E2), f(E1, E2+E3) = f(E1, E2)+f(E1, E3). Multilinear forms are, informally, essentially tensors of rank (0, n). That is Tij...k*uivj...wk=f(u, v, ..., w) for an appropriate absolute tensor T.
Note: Determinant
of a square matrix A, det A=![]() .
.
Section 4: Metric Tensor
An inner product between two
vectors u and v, a real number <u, v>, is defined
such that <u, v> = <v, u>, <u + w,
v> = <u, v> + <w, v>, u≠0⇒∃w <u,
w>≠0. Metric
tensor, g≡<Ei,
Ej>EiEj. Conjugate metric tensor, g, is
such that gijgjk=![]() . Metric is
a smooth (that is infinitely differentiable) tensor field made of metric
tensors. Geometry of any space with inner product--including distance, angles,
and curvature--is entirely determined by the metric. Length squared, ||u||2≡<u, u>.
Note that for some spaces ||u||2 can be zero or even negative
for nonzero u. Metric is called positive definitive if in all
cases <u, u> ≤
0. An associate tensor to tensor T is a tensor to which T can be transformed
through inner product(s) with metric tensor and/or conjugate metric tensor. Example:
gabTa=Tb.
. Metric is
a smooth (that is infinitely differentiable) tensor field made of metric
tensors. Geometry of any space with inner product--including distance, angles,
and curvature--is entirely determined by the metric. Length squared, ||u||2≡<u, u>.
Note that for some spaces ||u||2 can be zero or even negative
for nonzero u. Metric is called positive definitive if in all
cases <u, u> ≤
0. An associate tensor to tensor T is a tensor to which T can be transformed
through inner product(s) with metric tensor and/or conjugate metric tensor. Example:
gabTa=Tb.
Note: Outside of relativity, inner product is defined so that <u, u> ≥ 0.
Theorem: (a) gab is an absolute tensor of rank (0, 2); (b) gab=gba; (c) if metric tensor exists, conjugate metric tensor also exists; (d) gabuavb = <u, v>. (e) For every symmetric tensor g such that the matrix gij is invertible, there exists an inner product such that gabuavb = <u, v>. (f) If metric is positive definitive, <u, u> = 0⇔u=0.
Section 5: Manifolds
Definition: n-dimensional smooth manifold is a set of points combined with a set of coordinate systems such that:
1. Every coordinate system (also called smooth chart) consists of a subset R of the manifold and (x1, x2, ..., xn) for each point in R. All xi are real numbers.
2. In every coordinate system, different points have different coordinates.
3. Every coordinate system is open and connected. Open means that for each (x1, x2, ..., xn) in the system there exists r>0 such that every (y1, y2, ..., yn) belongs to the coordinate system provided that (xi-yi)*(xi-yi)<r*r. Connected means that for every pair of coordinates y=(y1, y2, ..., yn) and z=(z1, z2, ..., zn), there exists a continuous function f(t)= (x1, x2, ..., xn)(t) (where 0≤t≤1, and each (x1, x2, ..., xn) are valid coordinates for the coordinate system) such that f(0)=y and f(1)=z.
4. Union of all R is the set of points that make up the manifold.
5. For every 2 coordinate systems that share some of the points, the transformation between the coordinate systems must be smooth (that is infinitely differentiable) and thus have a nonzero Jacobian.
6. For every 2 points A and B, there exists A1, A2, ..., An such that A1=A, An=B, and for every integer i (0<i<n) there exists a coordinate system such that Ai and Ai+1 belong to the system. In other words, the manifold is connected.
Manifold is, informally, a generalization of a smooth surface or a space. Once a manifold is defined, more coordinate systems can be added provided that the Jacobian of all coordinate transformations exists and is nonzero at all points where the coordinates apply. Two manifolds are called topologically equivalent if there is a one-to-one transformation between the manifolds that preserves continuity. For example, all 2-dimensional ellipsoids are topologically equivalent, but a sphere is not topologically equivalent to a torus. Tensor field on a manifold is specified by specifying the field for every coordinate system such that the tensors obey the transformation equation.
Definition: Pseudo-Riemannian manifold is a smooth
manifold with a metric.
Definition: Riemannian manifold is a pseudo-Riemannian manifold whose
metric is positive definitive.
Section 6: Covariant Differentiation and Curvature
The actual change with location of a quantity depends not only on the change its coordinate components but also on the change of nature (size) of coordinates with location. For example, decrease of length of x1 (derived from g11) with increasing x2 can give incorrect results because ∂x1/∂x2=0 despite the change in lengths. Therefore, tensor differentiation is adjusted for the coordinates:
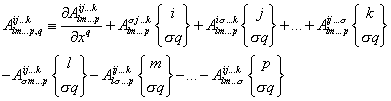
where Christoffel symbol of the
second kind, 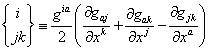 =gia
*[jk, a] and Christoffel symbol of the first kind, [ac, b]
≡
=gia
*[jk, a] and Christoffel symbol of the first kind, [ac, b]
≡![]() . Covariant (the
adjusted differentiation is called covariant) derivative of an absolute tensor
of rank (m, n) is an absolute tensor of rank (m, n+1). The
derivatives are denoted by adding a comma after the last subscript (such as Ai,j)
and placing the number of the axis/coordinate after the comma. Second and
higher derivatives do not require additional commas: Ai,jk.
The derivative is a linear operator. Covariant derivative, especially of a
scalar, is sometimes called gradient: B=∇A
means Bi=A,i. Theorem: gij,k=0.
The theorem confirms that derivatives are adjusted for the change in coordinate
size--that is the metric.
. Covariant (the
adjusted differentiation is called covariant) derivative of an absolute tensor
of rank (m, n) is an absolute tensor of rank (m, n+1). The
derivatives are denoted by adding a comma after the last subscript (such as Ai,j)
and placing the number of the axis/coordinate after the comma. Second and
higher derivatives do not require additional commas: Ai,jk.
The derivative is a linear operator. Covariant derivative, especially of a
scalar, is sometimes called gradient: B=∇A
means Bi=A,i. Theorem: gij,k=0.
The theorem confirms that derivatives are adjusted for the change in coordinate
size--that is the metric.
A smooth curve
is defined by a smooth function r(t)=(x1(t), x2(t),
..., xn(t)). The curve is called normalized if ||dr/dt||=1 or
||dr/dt||=-1 for every t on an open interval. Intrinsic derivative along
a curve, ![]() and
is used instead of the non-adjusted derivative to compensate for the change of
coordinate sizes and angles.
and
is used instead of the non-adjusted derivative to compensate for the change of
coordinate sizes and angles.
Curvature (more precisely intrinsic
curvature of the manifold) at a point is fully described by the Riemann
Christoffel Tensor: ![]() .
.
Rabcd≡gauRubcd. Theorem: Rabcd =-Rbacd=Rdcba; Rabcd+Radbc+Racdb=0; Rabcd,e+ Rabec,d+ Rabde,c=0.
Theorem: For every point in every pseudo-Riemannian manifold, there exists a coordinate system (called geodesic coordinate system) for which ∂gij/∂xk (and thus all of the Christoffel symbols) are zero at the point.
Part II: General Theory of Relativity
Section 1: Geometry of space-time.
Our world is modeled by a 4-dimensional pseudo-Riemannian manifold called space-time. For every point, there exists a frame of reference, that is a coordinate system, such that in the frame at that point, the metric, g=η where η≡E1E1+E2E2+E3E3-E4E4. Such frame of reference is called locally normal. If g=η and ∂gab/∂xc=0, the frame of reference (for each point, such frame can be proven to exist) is called locally inertial. MCRF is a locally normal frame of reference where the point object is currently at rest.
To be a complete theory, the mathematical model must be related to human perception. If g= η, x4=A4E4 refers to a point in time and AiEi = (x1, x2, x3) (i=1, 2, 3) refers to a location in space. Let an observer be at rest in a locally inertial frame of reference. The observer will locally define distance in space between (x1, x2, x3) and (y1, y2, y3) as √((x1-y1)2+(x2-y2)2+(x3-y3)2) and interval in time between x4 and y4 as |x4-y4|. Observers disagreeing on who is at rest may disagree about distance in space and interval in time. An observer at time t tends to consider space at time T>t as the future (and not yet occurring), space at T=t to be the present real world, and space at T<t as the past (what has already happened) provided that the direction of time is positive; otherwise, reverse '<' and '>'.
If g→η at xi and d→0, then V(R)/(d)3→1, where V(R) is volume in space of all points ri such that xi<ri<xi+d (i=1, 2, 3). For a property F based on a region of space, its density is dF/dV.
Section 2: Dynamics of Point Objects
A point object is a useful approximation for objects whose size that is small compared to the distance between the objects. It is described by its smooth curve: r(t). (t is a parameter, r4 is time; two curves r(s) and R(t) are equivalent if and only if there exists invertible s(t) such that r(s(t))=R(t).) Four-velocity, u≡dr/dt where r(t) is normalized. Observation shows that when u exists, ||u||=-1: Objects cannot move in space faster than they move forward in time. 4-velocity is undefined if the curve cannot be normalized. 4-velocity is used because objects move not only in space but also in time. Note: If g=η, 3‑velocity, v=(u1, u2, u3)/u4. Theorem: (1) MCRF exists unless u is undefined (2) u is a contravariant vector with value (0, 0, 0, 1) in any MCRF.
For a normalized curve, acceleration (a) is the intrinsic derivative of the velocity. When a particle does not interact, its a is 0, and it is said to move on a geodesic. (If the curve cannot be normalized, a=0 when for an appropriate invertible s(t), δr(s(t))/δs=0.) Light has undefined 4-velocity and zero acceleration. Since an event cannot cause itself, for every smooth curve r(s) with ||u||=-1 at all points, s≠t ⇒ r(s)≠r(t).
Rest mass (an absolute scalar m0) is mass in MCRF. 4-momentum, p ≡ m0u. p is a contravariant vector; ||p||2=-(m0)2. If g=η, the first 3 components form the usual momentum and the 4th component is energy (energy is relativistic mass). 4‑momentum for a set of non-intersecting objects is defined as the sum of 4-momentums for all objects in the set--p is additive. Force is intrinsic derivative of the momentum (assuming that the curve is normalized). When acceleration is zero, force is zero.
Section 3: Relativistic Fluids
Since all objects have sizes, point objects are impossible. Instead, the universe is modeled by tensor fields (sometimes called fluids) such as the stress-energy tensor (Tab). If a part of the world is modeled by tensor field A and A is sum of Bs, then each B is called an element of A. Thus, each tensor field is additive for all of its elements. Let 4-momentum density in space (a vector) be denoted P. For a uniform element of 4-velocity U, T=U⊗P (caution: elements of P do not match with elements of T); ‑gabTab is rest mass density. For an element, the force density, Fa=Tab,b (spatial components are pressure and the time component is density of power). Force density is based on area in space on which the force is acting. The task in non-quantum physics is to use some information about tensor fields to obtain more information.
Section 4: Gravitation and the Foundations of Relativity
Gravitation is represented by curvature of space-time. Ricci's tensor, Rbd = Rabad; Rab=gaugbvRuv. Einstein's tensor is Gab=Rab-½gabgcdRcd.
(Postulate) Einstein's Field Equation: G=8πT.
Theorem: (a) Gab=Gba; (b) Gab,b=0.
Corollary: (a) Tab=Tba; (b) Tab,b=0.
Interpretation of part (b) of the corollary:
1. Locally, energy and momentum are conserved.
2. Whenever two elements interact, the change of T for element A due to element B is exactly opposite to the change of T for element B due to element A.
General relativity is a template model--it specifies how interactions can be described but does not state all equations for all interactions. An interaction is specified by stating the type of tensor fields matter and the interaction have, the equations for the tensor fields, stress-energy tensor of the interaction field, and force density on the element by the field. All equations are expressed in terms of the tensors (including the metric g) through addition, contraction, products, covariant differentiation, and operations derived from these operations. Index variables but not specific index values may be used, and no variable in an expression may appear twice as a subscript or a superscript (except when separated by '+' in the expanded form).
Theorem: (It is stated informally. It is also called Principle of Equivalence)
1. Physical laws are the same in all frames of reference.
2. Other operations on tensors may not be included in the equations
3. Physical laws are local (no actions at a distance)
Justification of part (1): The expressions transform as the appropriate tensors do.
An implication of part (2): Riemann Christoffel tensor (derived from the metric through non-adjusted differentiation and other operations) cannot be included.
Section 5: Laws of Electromagnetism
Let ji be electric current density in i direction where xi are coordinates of space where g=η; and let electric charge density, dq/dV=ρq. Then, 4-current, J = (j1, j2, j3, ρq), is a contravariant vector. For a uniform element, J=uρq. Electromagnetic field is characterized by Faraday's tensor: Fab. (Note: Fav=gvbFab; Fuv=guaFav.) The field obeys Fuv=-Fvu, Fuv,v=4πk*Ju and Fuv,w+ Fvw,u+ Fwu,v= 0, has stress-energy tensor Tuv = (FuaFva-guvFabFab/4)/(4πk), and force density on an element is Fc = FcaJa.
Note: Coulomb's constant, k=0.007297...ħc/e2= c2*10‑7(kilogram*meter)/(coulomb)2.
Theorem: Ja,a=0. Interpretation: Electric charge can move but cannot be created or destroyed.
Section 6: Concluding Remarks
A non-quantum physical model is called complete if, given an initial state of the system, its development in time can be (theoretically) fully predicted. Theorem: Gravitation and electromagnetism, as presented above, are complete. In addition to electromagnetism, user-defined interactions can be added to avoid using quantum mechanics: Such interactions usually describe macroscopic predictions of quantum mechanics. If the result of a calculation is in different units than you want the result to be, multiply and/or divide by the following conversion constants: c = 299792458 meter/second, G ≈ 6.67259*10‑11 (meter)3/(kilogram*(second)2). From this paper, you have learned the entire non-quantum physics in the sense that the knowledge that is not part of the paper can be derived from knowledge that is. However, theorems, relevant approximations in real-world situations, and practice are required to effectively solve problems.
Exercises
1. Show that C=A*B⇔Cik=AijBjk for all matrices A, B, and C.
2. For a tensor of rank (l, m) and weight W in n-dimensional space increase of coordinates in 'a' times increases the tensor components in 'b' times. Prove: W = (l-m+logba)/n.
3. How does coordinate change affect
(a) scalars (b) contravariant
vectors (c) covariant vectors
(d) tensors of rank (0, 2) (e) tensors of rank (2, 0) (f)
tensors of rank (1, 1).
4. Prove that (a) ![]() =det A where Aij=
=det A where Aij=![]() (b)
(b)![]() .
.
5. Show that ||u + v||2 = ||u||2 + ||v||2
+ 2 <u, v>.
6. In parts (a) and (b), show that the space is a Riemannian manifold.
(a) Euclidian n-dimensional space with metric gij=δij.
(b) The set of all x (0≤x<1)
such that coordinate system 1: 0<x<1, y1=x, and system 2:
0≤x<½, y2=x,
or ½<x<1, y2=x-1. For metric, g11=1 in both
coordinate systems.
Note: The manifold can be represented as a circle of circumference 1.
(c) Show that no appropriate coordinate system
can span the entire manifold in part (b).
7. For tensors in problem 3, find (a) covariant
derivative (b) intrinsic derivative.
8. For an arbitrary 2-dimensional orthogonal (g12=0)
coordinate system find
(a) All of the Christoffel symbols.
(b) Riemann Christoffel tensor in terms of the
metric.
Hint: Use symmetry in the equations to save time.
9. Lorentz transformation (of coordinates) is
(x1, x2, x3, x4)→((x1-vx4)/√(1-(v)2),
x2, x3, (x4-v*x1)/ √ (1-(v)2))
where ‑1<v<1.
(a) Show how Lorentz transformation affects tensors of rank (0, 2).
(b) Use your answer to (a) to prove that if g=η, then g=η after a Lorentz transformation.
10. Find T for a uniform element of momentum density
(px, 0, 0, E) where g=η.
11. Find Einstein's tensor (a) for metric in problem 7
(b) for an
arbitrary locally inertial (4-dimensional) coordinate system.
Note: Part (b) may be omitted because it may require a long
calculation.
Appendix: Preliminary Mathematics
Let x1,
x2, ..., xn be independent variables related to y1,
y2, ..., yn. Then, ![]() is the rate of change of yi
divided by rate of change of xj assuming that the other x
are held constant. ∂f/∂x is sometimes
denoted fx. Jacobian, J(x/y), is determinant of the
matrix whose cell of index ij is ∂xi/∂yj.
When coordinates work properly, the Jacobian is not zero.
is the rate of change of yi
divided by rate of change of xj assuming that the other x
are held constant. ∂f/∂x is sometimes
denoted fx. Jacobian, J(x/y), is determinant of the
matrix whose cell of index ij is ∂xi/∂yj.
When coordinates work properly, the Jacobian is not zero.
Let a space have
a measure based on a region (length, area (A(R)), and volume (V(R)) are
measures), m(R); and an additive function whose argument is a region:
F(R). Then, f(r) = dF/dm=limit as size of R→0 of F(R)/m(R) when
such limit exists, such that r always belongs to R. Then,![]() . Properties of
measure: m(R)≥
0; measure is additive, that is measure of two non-intersecting regions is sum
of measures of the regions. Note: dF/dm is sometimes called F
density. F(x) is continuous if as change in x→0, change in f(x)→0. df/dt ≡
f′(t) ≡ limit of (f(t+a)-f(t))/a
as a→0 for any
f(t) for which the limit exists. dn+1f/dtn+1=(dnf/dtn)/dt
with d0f/dt0=f(t). Function f is smooth if
for all positive integers n, dnf/dtn
exists. In phrases such as "a→b,
c→d",
symbol '→' means 'approaches
arbitrarily close to'.
. Properties of
measure: m(R)≥
0; measure is additive, that is measure of two non-intersecting regions is sum
of measures of the regions. Note: dF/dm is sometimes called F
density. F(x) is continuous if as change in x→0, change in f(x)→0. df/dt ≡
f′(t) ≡ limit of (f(t+a)-f(t))/a
as a→0 for any
f(t) for which the limit exists. dn+1f/dtn+1=(dnf/dtn)/dt
with d0f/dt0=f(t). Function f is smooth if
for all positive integers n, dnf/dtn
exists. In phrases such as "a→b,
c→d",
symbol '→' means 'approaches
arbitrarily close to'.
'√' is a symbol for square root. |x|=√(x)2. a≡b means a is defined to be equal to b.
π ≡ 1/1-1/3+1/5-1/7+1/9-.... ∃x means 'there exists x such that'. ∀x means 'for all x'. When ∃ or ∀ are used, parenthesis after the variable, if present, indicate restrictions on the values of the variable. 0 is a zero vector (or matrix or tensor), that is a vector whose all components are zero. A permutation is any rearrangement (including no rearrangement at all). Permutation is called even if it can be done using an even number of interchanges and odd if it can be done using an odd number of interchanges. Theorem: no permutation is both even and odd.
'A⇒B' means 'A implies B', and 'A⇔B' means 'A⇒B and B⇒A'.