5 Troubleshooting

5.0.0.1 pw.x says 'error while loading shared libraries' or 'cannot open shared object file' and does not start

Possible reasons:

• If you are running on the same machines on which the code was compiled, this is a library configuration problem. The solution is machine-dependent. On Linux, find the path to the missing libraries; then either add it to file /etc/ld.so.conf and run ldconfig (must be done as root), or add it to variable LD_LIBRARY_PATH and export it. Another possibility is to load non-shared version of libraries (ending with .a) instead of shared ones (ending with .so).
• If you are not running on the same machines on which the code was compiled: you need either to have the same shared libraries installed on both machines, or to load statically all libraries (using appropriate configure or loader options). The same applies to Beowulf-style parallel machines: the needed shared libraries must be present on all PCs.

5.0.0.2 errors in examples with parallel execution

If you get error messages in the example scripts - i.e. not errors in the codes - on a parallel machine, such as e.g.: run example: -n: command not found you may have forgotten to properly define PARA_PREFIX and PARA_POSTFIX.

5.0.0.3 pw.x prints the first few lines and then nothing happens (parallel execution)

If the code looks like it is not reading from input, maybe it isn't: the MPI libraries need to be properly configured to accept input redirection. Use pw.x -i and the input file name (see Sec.4.4), or inquire with your local computer wizard (if any). Since v.4.2, this is for sure the reason if the code stops at Waiting for input....

5.0.0.4 pw.x stops with error while reading data

There is an error in the input data, typically a misspelled namelist variable, or an empty input file. Unfortunately with most compilers the code just reports Error while reading XXX namelist and no further useful information. Here are some more subtle sources of trouble:

• Out-of-bound indices in dimensioned variables read in the namelists;
• Input data files containing ^M (Control-M) characters at the end of lines, or non-ASCII characters (e.g. non-ASCII quotation marks, that at a first glance may look the same as the ASCII character). Typically, this happens with files coming from Windows or produced with "smart" editors.

Both may cause the code to crash with rather mysterious error messages. If none of the above applies and the code stops at the first namelist (&CONTROL) and you are running in parallel, see the previous item.

5.0.0.5 pw.x mumbles something like cannot recover or error reading recover file

You are trying to restart from a previous job that either produced corrupted files, or did not do what you think it did. No luck: you have to restart from scratch.

5.0.0.6 pw.x stops with inconsistent DFT error

As a rule, the flavor of DFT used in the calculation should be the same as the one used in the generation of pseudopotentials, which should all be generated using the same flavor of DFT. This is actually enforced: the type of DFT is read from pseudopotential files and it is checked that the same DFT is read from all PPs. If this does not hold, the code stops with the above error message. Use - at your own risk - input variable input_dft to force the usage of the DFT you like.

5.0.0.7 pw.x stops with error in cdiaghg or rdiaghg

Possible reasons for such behavior are not always clear, but they typically fall into one of the following cases:

• serious error in data, such as bad atomic positions or bad crystal structure/supercell;
• a bad pseudopotential, typically with a ghost, or a USPP giving non-positive charge density, leading to a violation of positiveness of the S matrix appearing in the USPP formalism;
• a failure of the algorithm performing subspace diagonalization. The LAPACK algorithms used by cdiaghg (for generic k-points) or rdiaghg (for $\Gamma$ - only case) are very robust and extensively tested. Still, it may seldom happen that such algorithms fail. Try to use conjugate-gradient diagonalization (diagonalization='cg'), a slower but very robust algorithm, and see what happens.
• buggy libraries. Machine-optimized mathematical libraries are very fast but sometimes not so robust from a numerical point of view. Suspicious behavior: you get an error that is not reproducible on other architectures or that disappears if the calculation is repeated with even minimal changes in parameters. Known cases: HP-Compaq alphas with cxml libraries, Mac OS-X with system BLAS/LAPACK. Try to use compiled BLAS and LAPACK (or better, ATLAS) instead of machine-optimized libraries.

5.0.0.8 pw.x crashes with no error message at all

This happens quite often in parallel execution, or under a batch queue, or if you are writing the output to a file. When the program crashes, part of the output, including the error message, may be lost, or hidden into error files where nobody looks into. It is the fault of the operating system, not of the code. Try to run interactively and to write to the screen. If this doesn't help, move to next point.

5.0.0.9 pw.x crashes with segmentation fault or similarly obscure messages

Possible reasons:

• too much RAM memory or stack requested (see next item).
• if you are using highly optimized mathematical libraries, verify that they are designed for your hardware.
• If you are using aggressive optimization in compilation, verify that you are using the appropriate options for your machine
• The executable was not properly compiled, or was compiled on a different and incompatible environment.
• buggy compiler or libraries: this is the default explanation if you have problems with the provided tests and examples.

5.0.0.10 pw.x works for simple systems, but not for large systems or whenever more RAM is needed

Possible solutions:

• Increase the amount of RAM you are authorized to use (which may be much smaller than the available RAM). Ask your system administrator if you don't know what to do. In some cases the stack size can be a source of problems: if so, increase it with command limits or ulimit).
• Reduce nbnd to the strict minimum (for insulators, the default is already the minimum, though).
• Reduce the work space for Davidson diagonalization to the minimum by setting diago_david_ndim=2; also consider using conjugate gradient diagonalization (diagonalization='cg'), slow but very robust, which requires almost no work space.
• If the charge density takes a significant amount of RAM, reduce mixing_ndim from its default value (8) to 4 or so.
• In parallel execution, use more processors, or use the same number of processors with less pools. Remember that parallelization with respect to k-points (pools) does not distribute memory: only parallelization with respect to R- (and G-) space does.
• If none of the above is sufficient or feasible, you have to either reduce the cutoffs and/or the cell size, or to use a machine with more RAM.

5.0.0.11 pw.x crashes with error in davcio

davcio is the routine that performs most of the I/O operations (read from disk and write to disk) in pw.x; error in davcio means a failure of an I/O operation.

• If the error is reproducible and happens at the beginning of a calculation: check if you have read/write permission to the scratch directory specified in variable outdir. Also: check if there is enough free space available on the disk you are writing to, and check your disk quota (if any).
• If the error is irreproducible: your might have flaky disks; if you are writing via the network using NFS (which you shouldn't do anyway), your network connection might be not so stable, or your NFS implementation is unable to work under heavy load
• If it happens while restarting from a previous calculation: you might be restarting from the wrong place, or from wrong data, or the files might be corrupted. Note that, since QE 5.1, restarting from arbitrary places is no more supported: the code must terminate cleanly.
• If you are running two or more instances of pw.x at the same time, check if you are using the same file names in the same temporary directory. For instance, if you submit a series of jobs to a batch queue, do not use the same outdir and the same prefix, unless you are sure that one job doesn't start before a preceding one has finished.

5.0.0.12 pw.x crashes in parallel execution with an obscure message related to MPI errors

Random crashes due to MPI errors have often been reported, typically in Linux PC clusters. We cannot rule out the possibility that bugs in QUANTUM ESPRESSO cause such behavior, but we are quite confident that the most likely explanation is a hardware problem (defective RAM for instance) or a software bug (in MPI libraries, compiler, operating system).

Debugging a parallel code may be difficult, but you should at least verify if your problem is reproducible on different architectures/software configurations/input data sets, and if there is some particular condition that activates the bug. If this doesn't seem to happen, the odds are that the problem is not in QUANTUM ESPRESSO. You may still report your problem, but consider that reports like it crashes with...(obscure MPI error) contain 0 bits of information and are likely to get 0 bits of answers.

5.0.0.13 pw.x stops with error message the system is metallic, specify occupations

You did not specify state occupations, but you need to, since your system appears to have an odd number of electrons. The variable controlling how metallicity is treated is occupations in namelist &SYSTEM. The default, occupations='fixed', occupies the lowest (N electrons)/2 states and works only for insulators with a gap. In all other cases, use 'smearing' ('tetrahedra' for DOS calculations). See input reference documentation for more details.

5.0.0.14 pw.x stops with internal error: cannot bracket Ef

Possible reasons:

• serious error in data, such as bad number of electrons, insufficient number of bands, absurd value of broadening;
• the Fermi energy is found by bisection assuming that the integrated DOS N(E ) is an increasing function of the energy. This is not guaranteed for Methfessel-Paxton smearing of order 1 and can give problems when very few k-points are used. Use some other smearing function: simple Gaussian broadening or, better, Marzari-Vanderbilt 'cold smearing'.

5.0.0.15 pw.x yields internal error: cannot bracket Ef message but does not stop

This may happen under special circumstances when you are calculating the band structure for selected high-symmetry lines. The message signals that occupations and Fermi energy are not correct (but eigenvalues and eigenvectors are). Remove occupations='tetrahedra' in the input data to get rid of the message.

5.0.0.16 pw.x runs but nothing happens

Possible reasons:

• in parallel execution, the code died on just one processor. Unpredictable behavior may follow.
• in serial execution, the code encountered a floating-point error and goes on producing NaNs (Not a Number) forever unless exception handling is on (and usually it isn't). In both cases, look for one of the reasons given above.
• maybe your calculation will take more time than you expect.

5.0.0.17 pw.x yields weird results

If results are really weird (as opposed to misinterpreted):

• if this happens after a change in the code or in compilation or preprocessing options, try make clean, recompile. The make command should take care of all dependencies, but do not rely too heavily on it. If the problem persists, recompile with reduced optimization level.
• maybe your input data are weird.

5.0.0.18 FFT grid is machine-dependent

Yes, they are! The code automatically chooses the smallest grid that is compatible with the specified cutoff in the specified cell, and is an allowed value for the FFT library used. Most FFT libraries are implemented, or perform well, only with dimensions that factors into products of small numbers (2, 3, 5 typically, sometimes 7 and 11). Different FFT libraries follow different rules and thus different dimensions can result for the same system on different machines (or even on the same machine, with a different FFT). See function allowed in Modules/fft_scalar.f90.

As a consequence, the energy may be slightly different on different machines. The only piece that explicitly depends on the grid parameters is the XC part of the energy that is computed numerically on the grid. The differences should be small, though, especially for LDA calculations.

Manually setting the FFT grids to a desired value is possible, but slightly tricky, using input variables nr1, nr2, nr3 and nr1s, nr2s, nr3s. The code will still increase them if not acceptable. Automatic FFT grid dimensions are slightly overestimated, so one may try very carefully to reduce them a little bit. The code will stop if too small values are required, it will waste CPU time and memory for too large values.

Note that in parallel execution, it is very convenient to have FFT grid dimensions along z that are a multiple of the number of processors.

5.0.0.19 pw.x does not find all the symmetries you expected

pw.x determines first the symmetry operations (rotations) of the Bravais lattice; then checks which of these are symmetry operations of the system (including if needed fractional translations). This is done by rotating (and translating if needed) the atoms in the unit cell and verifying if the rotated unit cell coincides with the original one.

Assuming that your coordinates are correct (please carefully check!), you may not find all the symmetries you expect because:

• the number of significant figures in the atomic positions is not large enough. In file PW/eqvect.f90, the variable accep is used to decide whether a rotation is a symmetry operation. Its current value (10^-5 ) is quite strict: a rotated atom must coincide with another atom to 5 significant digits. You may change the value of accep and recompile.
• they are not acceptable symmetry operations of the Bravais lattice. This is the case for C₆₀ , for instance: the I_h icosahedral group of C₆₀ contains 5-fold rotations that are incompatible with translation symmetry.
• the system is rotated with respect to symmetry axis. For instance: a C₆₀ molecule in the fcc lattice will have 24 symmetry operations (T_h group) only if the double bond is aligned along one of the crystal axis; if C₆₀ is rotated in some arbitrary way, pw.x may not find any symmetry, apart from inversion.
• they contain a fractional translation that is incompatible with the FFT grid (see next paragraph). Note that if you change cutoff or unit cell volume, the automatically computed FFT grid changes, and this may explain changes in symmetry (and in the number of k-points as a consequence) for no apparent good reason (only if you have fractional translations in the system, though).
• a fractional translation, without rotation, is a symmetry operation of the system. This means that the cell is actually a supercell. In this case, all symmetry operations containing fractional translations are disabled. The reason is that in this rather exotic case there is no simple way to select those symmetry operations forming a true group, in the mathematical sense of the term.

5.0.0.20 Warning: symmetry operation # N not allowed

This is not an error. If a symmetry operation contains a fractional translation that is incompatible with the FFT grid, it is discarded in order to prevent problems with symmetrization. Typical fractional translations are 1/2 or 1/3 of a lattice vector. If the FFT grid dimension along that direction is not divisible respectively by 2 or by 3, the symmetry operation will not transform the FFT grid into itself. Solution: you can either force your FFT grid to be commensurate with fractional translation (set variables nr1, nr2, nr3 to suitable values), or set variable use_all_frac to .true., in namelist &SYSTEM. Note however that the latter is incompatible with hybrid functionals and with phonon calculations.

5.0.0.21 Self-consistency is slow or does not converge at all

Bad input data will often result in bad scf convergence. Please carefully check your structure first, e.g. using XCrySDen.

Assuming that your input data is sensible :

1. Verify if your system is metallic or is close to a metallic state, especially if you have few k-points. If the highest occupied and lowest unoccupied state(s) keep exchanging place during self-consistency, forget about reaching convergence. A typical sign of such behavior is that the self-consistency error goes down, down, down, than all of a sudden up again, and so on. Usually one can solve the problem by adding a few empty bands and a small broadening.
2. Reduce mixing_beta to 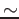$\sim$ 0.3 ÷ 0.1 or smaller. Try the mixing_mode value that is more appropriate for your problem. For slab geometries used in surface problems or for elongated cells, mixing_mode='local-TF' should be the better choice, dampening "charge sloshing". You may also try to increase mixing_ndim to more than 8 (default value). Beware: this will increase the amount of memory you need.
3. Specific to USPP: the presence of negative charge density regions due to either the pseudization procedure of the augmentation part or to truncation at finite cutoff may give convergence problems. Raising the ecutrho cutoff for charge density will usually help.

5.0.0.22 I do not get the same results in different machines!

If the difference is small, do not panic. It is quite normal for iterative methods to reach convergence through different paths as soon as anything changes. In particular, between serial and parallel execution there are operations that are not performed in the same order. As the numerical accuracy of computer numbers is finite, this can yield slightly different results.

It is also normal that the total energy converges to a better accuracy than its terms, since only the sum is variational, i.e. has a minimum in correspondence to ground-state charge density. Thus if the convergence threshold is for instance 10^-8 , you get 8-digit accuracy on the total energy, but one or two less on other terms (e.g. XC and Hartree energy). It this is a problem for you, reduce the convergence threshold for instance to 10^-10 or 10^-12 . The differences should go away (but it will probably take a few more iterations to converge).

5.0.0.23 Execution time is time-dependent!

Yes it is! On most machines and on most operating systems, depending on machine load, on communication load (for parallel machines), on various other factors (including maybe the phase of the moon), reported execution times may vary quite a lot for the same job.

5.0.0.24 Warning : N eigenvectors not converged

This is a warning message that can be safely ignored if it is not present in the last steps of self-consistency. If it is still present in the last steps of self-consistency, and if the number of unconverged eigenvector is a significant part of the total, it may signal serious trouble in self-consistency (see next point) or something badly wrong in input data.

5.0.0.25 Warning : negative or imaginary charge..., or ...core charge ..., or npt with rhoup< 0 ... or rho dw< 0 ...

These are warning messages that can be safely ignored unless the negative or imaginary charge is sizable, let us say of the order of 0.1. If it is, something seriously wrong is going on. Otherwise, the origin of the negative charge is the following. When one transforms a positive function in real space to Fourier space and truncates at some finite cutoff, the positive function is no longer guaranteed to be positive when transformed back to real space. This happens only with core corrections and with USPPs. In some cases it may be a source of trouble (see next point) but it is usually solved by increasing the cutoff for the charge density.

5.0.0.26 Structural optimization is slow or does not converge or ends with a mysterious bfgs error

Typical structural optimizations, based on the BFGS algorithm, converge to the default thresholds ( etot_conv_thr and forc_conv_thr ) in 15-25 BFGS steps (depending on the starting configuration). This may not happen when your system is characterized by "floppy" low-energy modes, that make very difficult (and of little use anyway) to reach a well converged structure, no matter what. Other possible reasons for a problematic convergence are listed below.

Close to convergence the self-consistency error in forces may become large with respect to the value of forces. The resulting mismatch between forces and energies may confuse the line minimization algorithm, which assumes consistency between the two. The code reduces the starting self-consistency threshold conv thr when approaching the minimum energy configuration, up to a factor defined by upscale. Reducing conv_thr (or increasing upscale) yields a smoother structural optimization, but if conv_thr becomes too small, electronic self-consistency may not converge. You may also increase variables etot_conv_thr and forc_conv_thr that determine the threshold for convergence (the default values are quite strict).

A limitation to the accuracy of forces comes from the absence of perfect translational invariance. If we had only the Hartree potential, our PW calculation would be translationally invariant to machine precision. The presence of an XC potential introduces Fourier components in the potential that are not in our basis set. This loss of precision (more serious for gradient-corrected functionals) translates into a slight but detectable loss of translational invariance (the energy changes if all atoms are displaced by the same quantity, not commensurate with the FFT grid). This sets a limit to the accuracy of forces. The situation improves somewhat by increasing the ecutrho cutoff.

5.0.0.27 pw.x stops during variable-cell optimization in checkallsym with non orthogonal operation error

Variable-cell optimization may occasionally break the starting symmetry of the cell. When this happens, the run is stopped because the number of k-points calculated for the starting configuration may no longer be suitable. Possible solutions:

• start with a nonsymmetric cell;
• use a symmetry-conserving algorithm: the Wentzcovitch algorithm (cell dynamics='damp-w') should not break the symmetry.