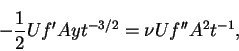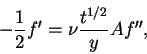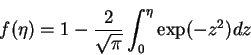Next: About this document ...
Up: No Title
Previous: No Title
We consider a flat plate of infinite extent which starts to move impulsively at t = 0 with a constant velocity U through fluid initially at rest. This is one of the simplest viscous flows which allows an exact solution as we will see. As the plate starts impulsively moving with constant speed U, due to the no slip condition at the plate surface, the fluid speed at the plate surface matches the plate speed U, but as we move away from the plate, the fluid velocity decreases towards zero (fluid at rest). Vorticity is generated at the plate surface and is diffused away from the plate. The change in the fluid velocity is confined to a layer close to the plate surface, which is called a boundary layer. As we are going to show, the boundary-layer thickness is proportional to
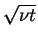 ,
where
,
where 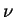 is the fluid kinematic viscosity, and it grows at a rate proportional to
is the fluid kinematic viscosity, and it grows at a rate proportional to
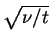 .
.
The equation of motion for this flow are the Navier-Stokes equations
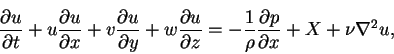 |
(1) |
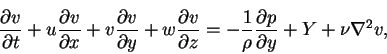 |
(2) |
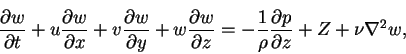 |
(3) |
and the continuity equation
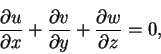 |
(4) |
where u,v and w are the flow velocity components, respectively, in the x,y and z directions. X,Y and Z are body forces, respectively, in the x,y and z directions. The fundamental difficulty in solving the Navier-Stokes equations (either exactly or approximately) is the non-linearity introduced by the convection terms in the momentum equations (1.1), (1.2) and (1.3). When the convective terms vanish, the resulting equations can be solved, which is the case for the present problem.
We consider that the plate lies in the plane y=0 and that the plate speed U is in the x direction. If we also assume v = w =0, an immediate consequence of the continuity equation (1.4) is that
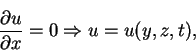 |
(5) |
so u is independent of x, and it then follows that all convection terms in equations (1.1), (1.2) and (1.3) vanishes. Assuming that any external force may be accounted for by measuring the pressure p from its hydrostatic value, the equations (1.1), (1.2) and (1.3) become
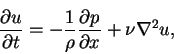 |
(6) |
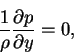 |
(7) |
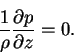 |
(8) |
Since, u is independent of x, we see that
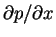 must be a function of t alone. This pressure gradient may be prescribed as an arbitrary function of t, then u(y,z,t) is determined by solving the linear equation (1.6). It should be noted that (1.6) is identical with the equation for heat conduction in two dimensions if the term
must be a function of t alone. This pressure gradient may be prescribed as an arbitrary function of t, then u(y,z,t) is determined by solving the linear equation (1.6). It should be noted that (1.6) is identical with the equation for heat conduction in two dimensions if the term
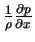 is interpreted as a uniform distribution of heat sources. Thus, known solutions in the theory of heat conduction may be taken over directly and interpreted as fluid flows. For the present problem, there is no prescribed pressure gradient and to simplify further we assume the flow two dimensional with x and y coordinates only. Now
u = u(y,t), and it satisfies the equation
is interpreted as a uniform distribution of heat sources. Thus, known solutions in the theory of heat conduction may be taken over directly and interpreted as fluid flows. For the present problem, there is no prescribed pressure gradient and to simplify further we assume the flow two dimensional with x and y coordinates only. Now
u = u(y,t), and it satisfies the equation
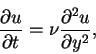 |
(9) |
with the initial condition
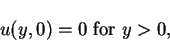 |
(10) |
and boundary condition
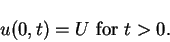 |
(11) |
To solve the initial boundary value problem we are going to obtain a similarity solution. The dependent variable is a function of two coordinates (x and t) and, moreover, they can be so chosen they are functions of a single elementary function of the coordinates. Then the unknown satisfy an ordinary differential equation. The existence of similarity solutions is often recognized by physical considerations, and in particular from deductions as to the forms of solutions which are possible dimensionally when the physical parameters in the problem do not provide both a fundamental length and a fundamental time. The emphasis is on these two units since, if such quantities appear, the unit of mass can always be derived from the density.
There is also a rather general method of testing for similarity solutions; it is most conveniently demonstrated by an example. For the present problem, in applying this method, we look for a one-parameter transformation of variables y,t and u under which the equations are invariant. a particularly useful transformation is
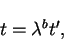 |
(12) |
where 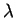 is the parameter. If we substitute the transformation (1.12) into equation (1.9), we obtain
is the parameter. If we substitute the transformation (1.12) into equation (1.9), we obtain
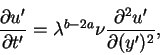 |
(13) |
and the requirement of invariance implies that
From the initial condition (1.11) we have that
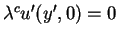 ,
and from the boundary condition (1.10) we have that
,
and from the boundary condition (1.10) we have that
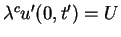 .
These two identities imply that
.
These two identities imply that
and the final transformation is
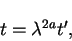 |
(16) |
Then, we can say that there exists a solution in which u is function of
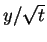 since each of this quantities is invariant in the transformation. We take
since each of this quantities is invariant in the transformation. We take
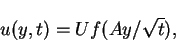 |
(17) |
and if we substitute this in equation (1.9), we obtain
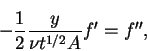 |
(18) |
and we chose
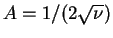 ,
and we define
,
and we define
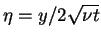 ,
such that we can write equation (1.18) in the form
,
such that we can write equation (1.18) in the form
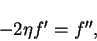 |
(19) |
which has solution of the form
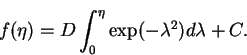 |
(20) |
In the limit
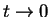 ,
we have
,
we have
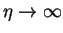 (consider y > 0), and the limit
(consider y > 0), and the limit
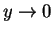 implies
implies
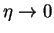 (consider t > 0). Then equation (1.10) implies that
(consider t > 0). Then equation (1.10) implies that
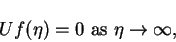 |
(21) |
and equation (1.11) implies that
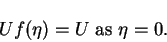 |
(22) |
If we impose these conditions to the solution given by equation (1.20), we obtain from equation (1.22) that
and from equation (1.21), we obtain that
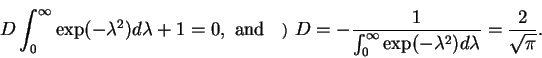 |
(24) |
Finally, we have
with
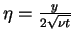 .
The final expression for u(y,t) is
.
The final expression for u(y,t) is
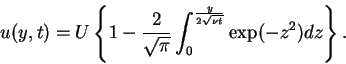 |
(25) |
From this equation for u(y,t), and if we define the boundary-layer thickness as the distance in which u drops to a given small fraction of U, we realize that the boundary-layer thickness is proportional to
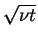 ,
and its growth rate is proportional to
,
and its growth rate is proportional to
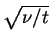 .
.
We provide an animation to illustrate the velocity profile given by equation (1.25) as function of y and t. In each frame of the animation we have a plot of u(y,t) for 0 < y <1 and t fixed. From frame to frame, we vary t from zero to a value t* such that
u(1,t) = 0.9U. This animation illustrates how the velocity profile varies as momentum is diffused away from the plate to the fluid.



Next: About this document ...
Up: No Title
Previous: No Title
Karl P Burr
2003-03-12
![]() ,
where
,
where ![]() is the fluid kinematic viscosity, and it grows at a rate proportional to
is the fluid kinematic viscosity, and it grows at a rate proportional to
![]() .
.