A Different Approach to Obtain $d\Gamma/dt$.

To proof Kelvin's theorem, we need to evaluate $d\Gamma/dt$, and in the proof above the representation of the integral as the limit of a finite sum was used to obtain the expression for $d\Gamma/dt$. Here we discuss how to obtain this expression using the definition of the derivative. We write

$$\frac{d\Gamma}{dt} = \lim_{\Delta t \rightarrow 0}\frac{\int_... ...x} -\int_{C(t)}\vec{v}(t,\vec{x}(t))\cdot d\vec{x}}{\Delta t}.$$ (9)

For a fluid particle at position $\vec{x}(t+\Delta t)$ (a point over the material contour $C(t+\Delta t)$), we can write in the limit $\Delta t \rightarrow 0$ that

$$\vec{x}(t+\Delta t) \approx \vec{x}(t)+\frac{d \vec{x}}{d t}(t)\Delta t + O((\Delta t)^{2}).$$ (10)

The speed $\vec{v}$ of a fluid particle at the position $\vec{x}$ is given by the equation

$$\frac{d\vec{x}}{dt}(t) = \vec{v}(t,\vec{x}(t)).$$ (11)

Therefore, equation (10) can be written in the form

$$\vec{x}(t+\Delta t) \approx \vec{x}(t)+\vec{v}(t,\vec{x}(t))\Delta t + O((\Delta t)^{2}).$$ (12)

This equation is illustrated in the figure below. In the limit $\Delta t \rightarrow 0$, the position $\vec{x}(t+\Delta t)$ (a point of the material contour $C(t+\Delta t)$) of a fluid particle at the instant $t+\Delta t$ can be approximated by its position $\vec{x}(t)$ (a point over the material contour C(t)) at instant t, plus what it has traveled during the time $\Delta t$. The distance traveled is given approximately by the vector $\vec{v}(t,\vec{x}(t))\Delta t$ with an error of order $O((\Delta t)^{2})$.

figure

 

Figure: Contours C(t) and $C(t+\Delta t)$. Illustration of the approximation for $\vec{x}(t+\Delta t)$.

According to equation (12), we can write

$$d\vec{x}(t+\Delta t) \approx d\vec{x}(t)+d\vec{v}(t,\vec{x}(t))\Delta t + O((\Delta t)^{2}).$$ (13)

The velocity vector $\vec{v}$ at the instant $t+\Delta t$ can be approximated in the same way as $\vec{x}(t+\Delta t)$ and $d\vec{x}(t+\Delta t)$. We can write

$$\vec{v}(t+\Delta t,\vec{x}(t+\Delta t)) \approx \vec{v}(t,\ve... ...{\partial t}(t,\vec{x}(t+\Delta t))\Delta t+O((\Delta t)^{2}).$$ (14)

If we substitute the approximate expression for $\vec{x}(t+\Delta t)$, given by equation (12), into equation (14), we obtain

$$\vec{v}(t+\Delta t,\vec{x}(t+\Delta t)) \approx \vec{v}(t,\ve... ...}(t)+\vec{v}(t,\vec{x}(t))\Delta t)\Delta t+O((\Delta t)^{2}).$$ (15)

Now we expand $\vec{v}$ in taylor series with respect to the second variable to obtain

$$\vec{v}(t+\Delta t,\vec{x}(t+\Delta t)) \approx \vec{v}(t,\ve... ...}\cdot\nabla \vec{v}(t,\vec{x}(t))\Delta t+ O((\Delta t)^{2}).$$ (16)

The expanssion above is illustrated in the figure below

According to equations (13) and (16), the integrand of the first integral in the right hand side of equation (9) can be approximated by the equation

$$\begin{split} \vec{v}(t+\Delta t,\vec{x}(t+\Delta t))\cdot d\... ...t d\vec{v}(t,\vec{x}(t))\Delta t+O((\Delta t)^{2}). \end{split}$$ (17)

Notice that the approximated form of the integrand of the first integral in the right hand side of equation (9), given above by equation (17), is now being evaluated over the contour C(t) instead of the contour $C(t+\Delta t)$. Therefore, we can write

$$\begin{split} \int_{C(t+\Delta t)}\vec{v}(t+\Delta t,\vec{x}(... ...c{v}(t,\vec{x}(t))\Delta t \\ & +O((\Delta t)^{2}). \end{split}$$ (18)

Now we can replace the first integral in the right hand side of equation (9) by the expression given in the equation (18). Therefore, the time derivative of the circulation is

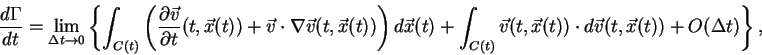$$\frac{d\Gamma}{dt} = \lim_{\Delta t \rightarrow 0}\left\{\int... ...t,\vec{x}(t))\cdot d\vec{v}(t,\vec{x}(t))+O(\Delta t)\right\},$$ (19)

and after the limit process is taking into account, we obtain

$$\frac{d\Gamma}{dt} = \int_{C(t)}\left(\frac{\partial \vec{v}}... ...+\int_{C(t)}\vec{v}(t,\vec{x}(t))\cdot d\vec{v}(t,\vec{x}(t)),$$ (20)

which is exactly the equation (7) we obtained using the previous approach.