Solution: 2D dipole with orientation angle .

Next: Solution: 3D dipole at Up: Dipole (doublet flow) Previous: Dipole (doublet flow)

Solution: 2D dipole with orientation angle $\alpha$ .

We derive the expression for a 2D dipole from the superposition of a source and a sink with the same strength and located a distance appart from each other. The superposition of the source and sink follows:

$\begin{displaymath}\phi(x,y) = \frac{m}{2\pi }\left[ \ln\sqrt {(x - a\cos\alpha)... ...\sqrt {(x + a\cos\alpha)^2 + (y+a\sin\alpha)^2} \right] \notag \end{displaymath}$

We take the limit $a \rightarrow 0$ . To preserve a finite effect from the two singularities as they are brought togheter, their strength must increase at the same time, for otherwise they will cancel out in the limit when they coincide. Thus it is necessary to make the product $\mu = 2ma$ a constant, with the result

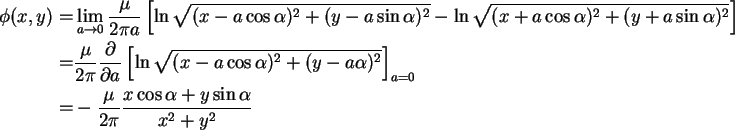
$\begin{align}\phi(x,y) = & \lim_{a \to 0} \frac{\mu}{2\pi a}\left[ \ln\sqrt {(x ... ...frac{\mu}{2\pi}\frac{x\cos \alpha + y\sin \alpha }{x^2 + y^2} \notag \end{align}$

NOTE: dipole $= \mu \frac{\partial }{\partial \xi }$ (unit source)