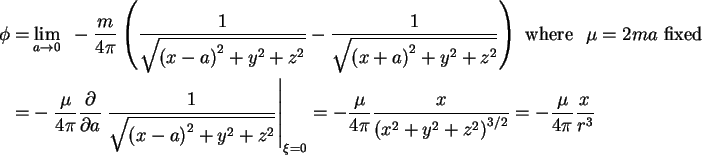We proceed the same way we did for the 2D dipole. We first write the superposition of a sorce and sink with the same strength ![]() and a distance
and a distance ![]() appart from each other. Then, we take the limit
appart from each other. Then, we take the limit
![]() .
In this limit process we keep the
.
In this limit process we keep the ![]() constant, otherwise the the source and sink cancel out in the limit.
constant, otherwise the the source and sink cancel out in the limit.