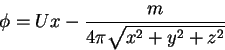Next: Solution: Position of the
Up: 3.7 - Simple Potential
Previous: Solution: 3D dipole at
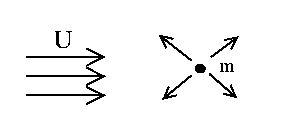
It is the superposition of a uniform
stream of constant speed 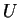 and a source of strength
and a source of strength
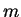 .
.
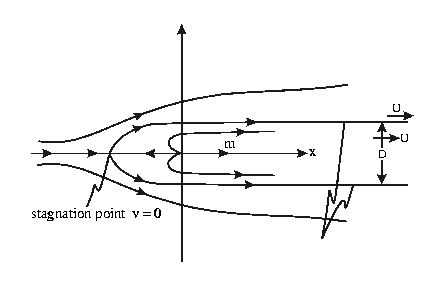
2D rankine half-body:
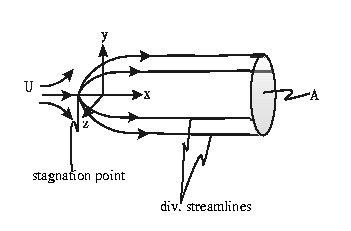
3D Rankine half-body:
- 1.
- Question: find the position
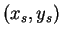 of the flow field stagnation point for the 2D Rankine half-body.
of the flow field stagnation point for the 2D Rankine half-body.
- (a)
- Hint: at the stagnation point
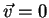 .
.
- (b)
- Hint: obtain the expression for
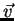 and set it equal to
and set it equal to 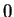 ,
and solve for
,
and solve for 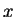 and
and 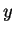 .
.
- 2.
- Question: evaluate the width
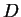 of the 2D rankine half-body.
of the 2D rankine half-body.
- (a)
- Hint: mass conservation
- 3.
- Question: find the position
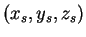 of the flow field stagnation point for the 3D Rankine half-body.
of the flow field stagnation point for the 3D Rankine half-body.
- (a)
- Hint: at the stagnation point
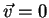 .
.
- (b)
- Hint: obtain the expression for
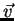 and set it equal to
and set it equal to 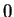 ,
and solve for
,
and solve for 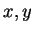 and
and 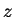 .
.
- 4.
- Question: evaluate the cross-sectional area
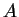 of the 3D rankine half-body.
of the 3D rankine half-body.
- (a)
- Hint: mass conservation
Keyword Search



Next: Solution: Position of the
Up: 3.7 - Simple Potential
Previous: Solution: 3D dipole at
![]() and a source of strength
and a source of strength
![]() .
.