From the expression for the potential, it is obvous that ![]() and
and ![]() .
So, we need to find
.
So, we need to find ![]() .
First, we obtain the
.
First, we obtain the ![]() component of the velocity vector.
component of the velocity vector.
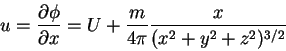
Now we set ![]() and solve for
and solve for ![]() .
We already know that
.
We already know that
![]() ,
so we set
,
so we set ![]() in the expression for
in the expression for ![]() to obtain
to obtain ![]() .
.
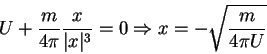 |
Therefore,
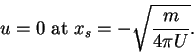 |