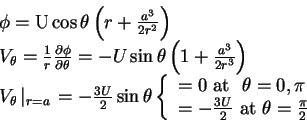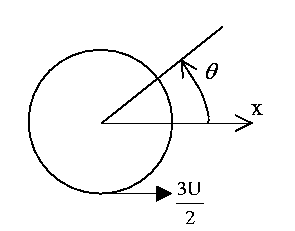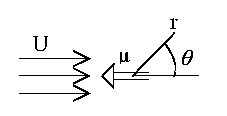
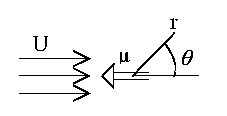
2D:
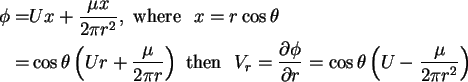
So ![]() on
on
![]() (which is the K.B.C. for a stationary
circle radius a) or choose
(which is the K.B.C. for a stationary
circle radius a) or choose
![]() .
.
Steady flow past a circle (U,a):
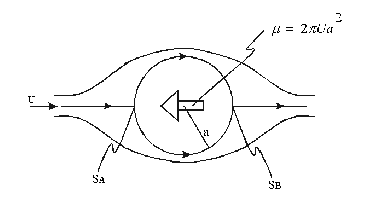
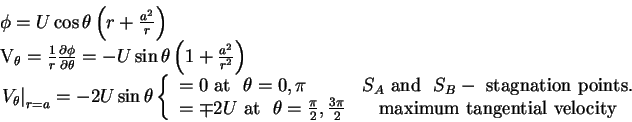 |
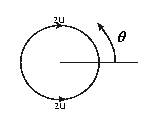
Illustration of the points where the flow reaches
maximum speed around the circle.
3D:
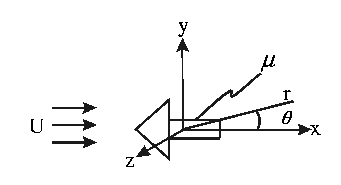
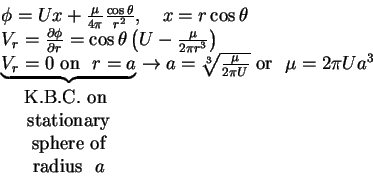
Steady flow past a sphere (U, a):