Next: 3.8 - Method of
Up: 3.7 - Simple Potential
Previous: Stream + Dipole: circles
Potential function:
Stream function:
Velocity vector components (polar coordinates):
- 1.
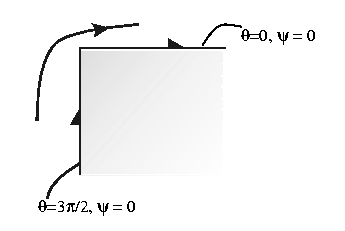
- interior corner flow - stagnation point origin:
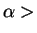 1.
1.
e.g. 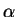 = 1,
= 1,
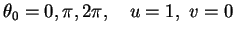
- 2.
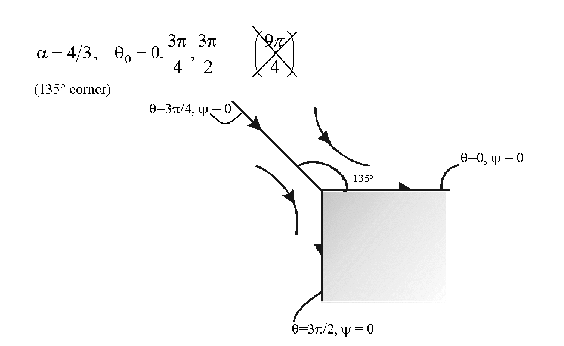
- Exterior corner flow,
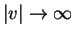 at origin:
at origin:
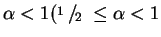 ).
).
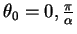 only. Since we
need
only. Since we
need
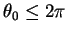 ,
we therefore require
,
we therefore require
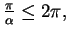 i.e.
i.e.
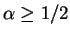 only.
only.
e.g.
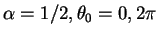 (
(
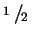 infinite plate,
flow around a tip)
infinite plate,
flow around a tip)
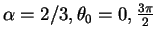 (
(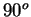 exterior corner)
exterior corner)
Keyword Search
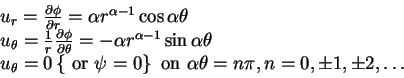
![]() = 1,
= 1,
![]()
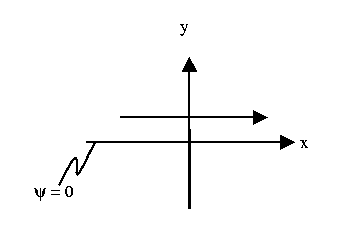
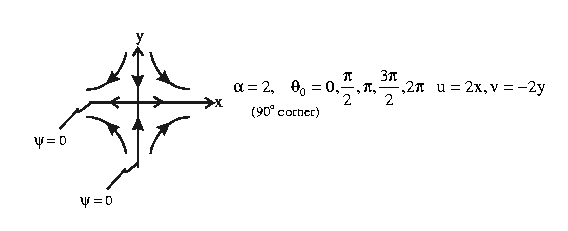
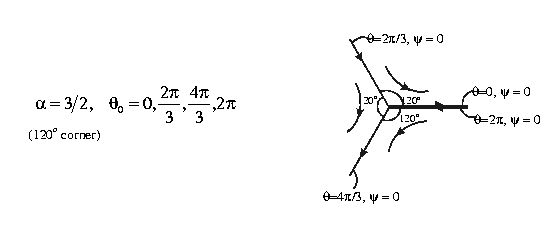
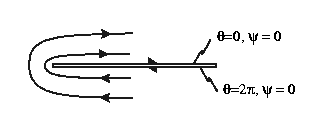
![]() (
(![]() exterior corner)
exterior corner)