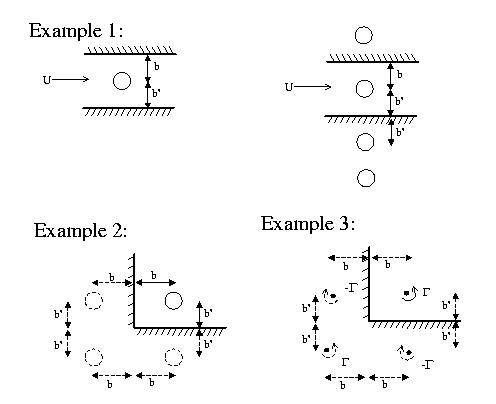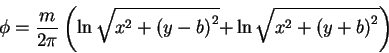
- 1.
- Question: verify that the boundary condition of no flux on the wall is satisfied.
- (a)
- Hint: no flux trough the wall
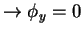 on
on 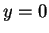 .
.
- (b)
- Hint: evaluate
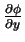 .
.
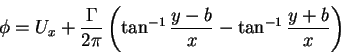
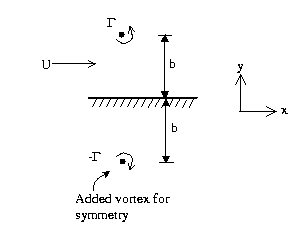
- 1.
- Question: verify that the boundary condition of no flux on the wall is satisfied.
- (a)
- Hint: no flux trough the wall
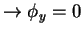 on
on 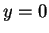 .
.
- (b)
- Hint: evaluate
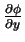 .
.
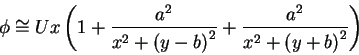
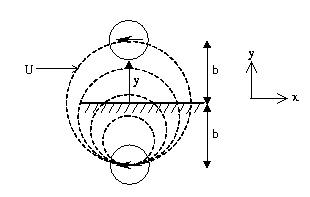
This solution satisfies the boundary condition on the
wall (
![]() ), and the degree it
satisfies the boundary condition of no flux through the circle
boundary increases as the ratio
), and the degree it
satisfies the boundary condition of no flux through the circle
boundary increases as the ratio ![]() ,
i.e., the velocity due
to the image dipole small on the real circle for
,
i.e., the velocity due
to the image dipole small on the real circle for ![]() .
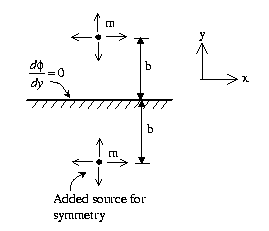
For a
2D dipole,
.
For a
2D dipole,
![]()
- 1.
- Question: verify the boundary condition of no flux at the wall.
- (a)
- Hint: evaluate the component of the velocity vector in the
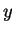 direction.
direction.
- (b)
- Hint: set
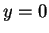 in the expression for the velocity vector in the
in the expression for the velocity vector in the 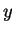 direction.
direction.
- More than one wall: