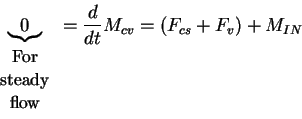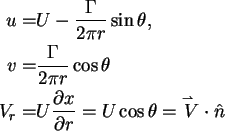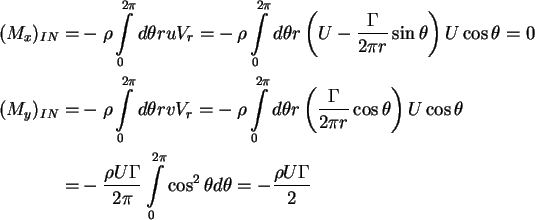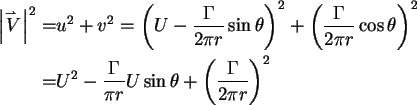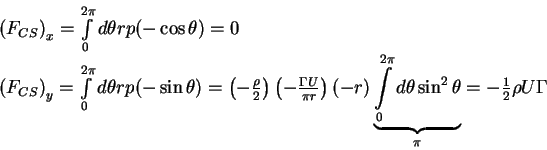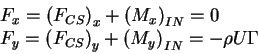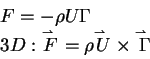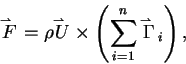Up: 3.8 - Method of
Previous: 3.9.2 Forces
Example: force on a vortex in a uniform
stream.
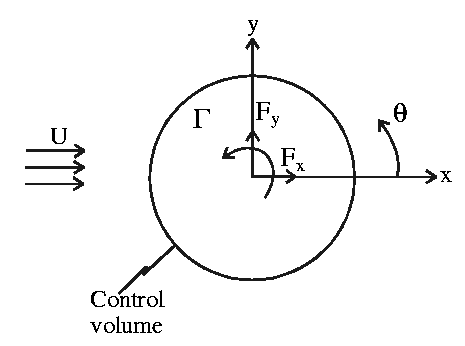
Consider a control surface in the form of a circle
radius R centered at the point vortex. Then according to Newton's
law:
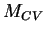 = Total (linear) momentum of control volume
= Total (linear) momentum of control volume
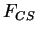 = Hydrodynamic force on CS by surrounding fluids
= Hydrodynamic force on CS by surrounding fluids
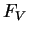 = Hydrodynamic force on CS by vortex = -(force on vortex
by fluid)
= Hydrodynamic force on CS by vortex = -(force on vortex
by fluid)
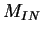 = net flux of momentum in CV through CS
= net flux of momentum in CV through CS
Therefore, force on vortex
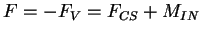 .
.
Momentum flux:
Evaluation of 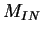 .
.
Pressure:
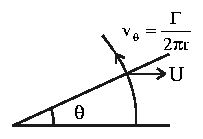
Velocity vector:
Force on the control surface - 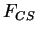 :
:
Finally,
i.e. the fluid exerts a downward force
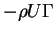 on the vortex
on the vortex
Kutta-Joukowski law:
Generalized Kutta-Joukowski Law:
where
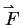 is the total force on a system of n vortices in a free
stream with speed
is the total force on a system of n vortices in a free
stream with speed 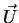 .
.
Keyword Search


Up: 3.8 - Method of
Previous: 3.9.2 Forces