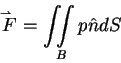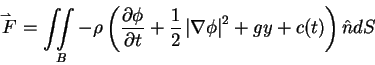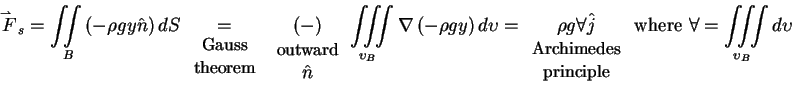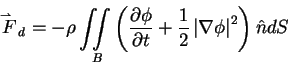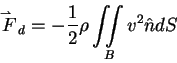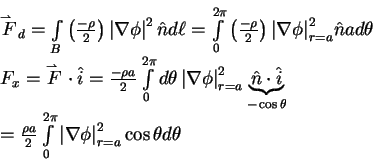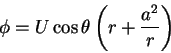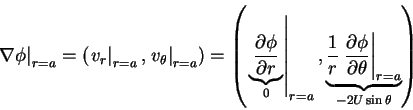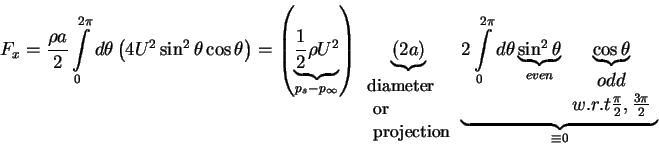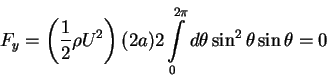Next: 3.10 Lift due to
Up: 3.9 Forces on a
Previous: 3.9.1 Fixed bodies &
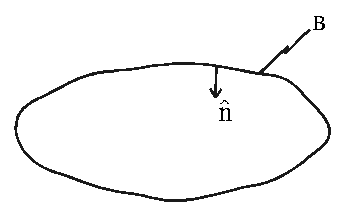
Total fluid force for
 flow:
flow:
For potential flow:
For the hydrostatic
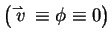 case:
case:
Hydrodynamic Force:
For steady
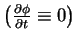 motion:
motion:
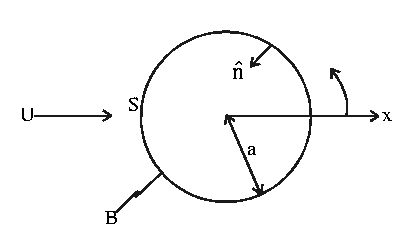
Example: Hydrodynamic force on 2D cylinder
in a steady uniform stream .
Potential function for the 2D cylinder:
Velocity vector on the 2D cylinder surface:
Square of the velocity vector on the 2D cylinder
surface:
Hydrodynamic force on the 2D cylinder:
Therefore, F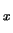 = 0 no forces ( symmetry fore-aft of
the streamlines). Similarly,
= 0 no forces ( symmetry fore-aft of
the streamlines). Similarly,
In fact, in general we find that
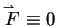 on any 2D or 3D body.
on any 2D or 3D body.
D'Alembert's ``paradox'':
No hydrodynamic force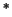 acts on a body moving
with constant translational velocity in an infinite, inviscid,
irrotational fluid.
acts on a body moving
with constant translational velocity in an infinite, inviscid,
irrotational fluid.
Note: The moment as measured in a local frame is not
necessarily zero.
Keyword Search



Next: 3.10 Lift due to
Up: 3.9 Forces on a
Previous: 3.9.1 Fixed bodies &

 flow:
flow: