We check if a 2D dipole oriented in the ![]() direction in a free stream of speed
direction in a free stream of speed ![]() plus its mirror image with respect to a wall at
plus its mirror image with respect to a wall at ![]() satisfy the no flux boundary condition at the wall. First, we obtain the
satisfy the no flux boundary condition at the wall. First, we obtain the
![]() ,
given by the equation
,
given by the equation
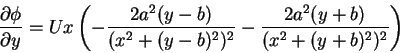 |
Next, we set ![]() ,
and
,
and
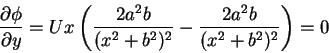 |