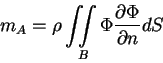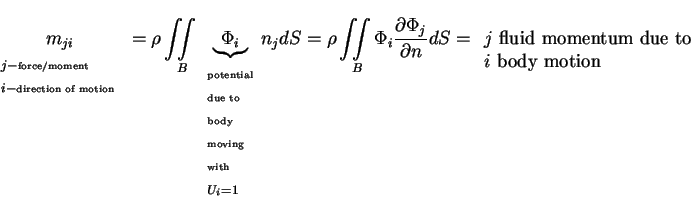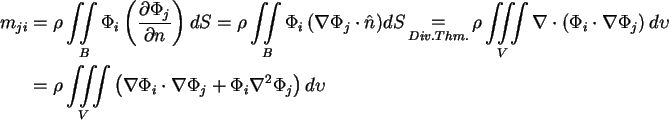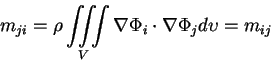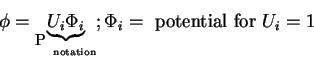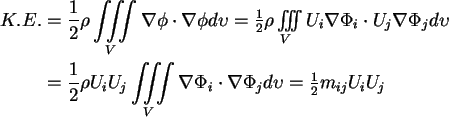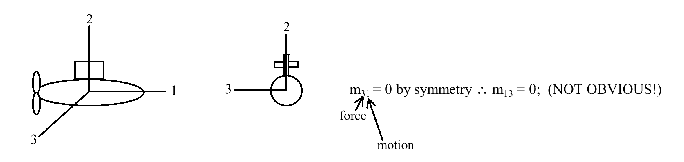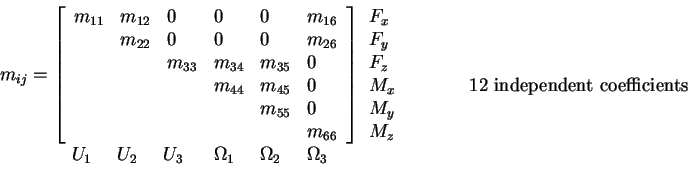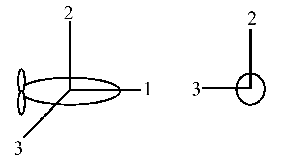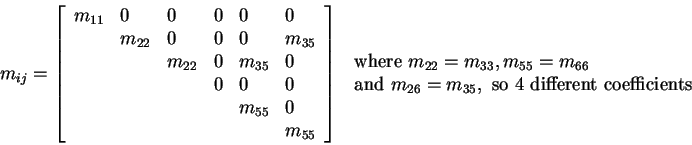Next: 3.12 - Slender body
13.021 - Marine Hydrodynamics, Fall 2003
Lecture 13
Copyright © 2003 MIT - Department of Ocean
Engineering,
All rights reserved.
13.021 - Marine Hydrodynamics
Lecture 13
Some Properties of Added-Mass Coefficients
- 1.
-
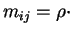 [function of geometry only]
[function of geometry only]
F, M = [linear function of 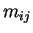 ]
]
 [function
of
[function
of

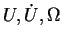 ]
]
- 2.
- Relationship to momentum of fluid:
Linear momentum
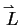 in
fluid:
in
fluid:
Force on fluid by body =
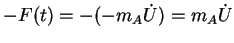 .
.
Therefore, 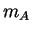 = total fluid momentum for body
moving at
= total fluid momentum for body
moving at 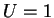 (regardless of how we get there from rest) =
fluid momentum per unit velocity of body.
(regardless of how we get there from rest) =
fluid momentum per unit velocity of body.
K.B.C.
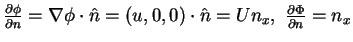 for
for 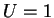 .
.
For general 6 DOF:
- 3.
- Symmetry of added mass matrix
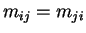 .
.
Therefore,
- 4.
- Relationship to kinetic energy of fluid. In general, for body motion
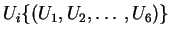 .
.
K.E. depends only on 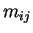 and instantaneous
and instantaneous 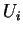 .
.
- 5.
- Use of symmetry to simplify
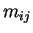 .
From 36
.
From 36
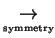 21
21 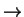 ?
Choose coordinate system so that some
?
Choose coordinate system so that some
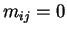 by symmetry.
e.g.
example 1: port-starboard symmetry (sym
w.r.t.
by symmetry.
e.g.
example 1: port-starboard symmetry (sym
w.r.t. 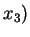
example 2: rotational (axi) sym. about
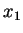
Exercise: How about 3 planes of symmetry (e.g.
a cuboid); a cube; a sphere?? Work out detail!



Next: 3.12 - Slender body
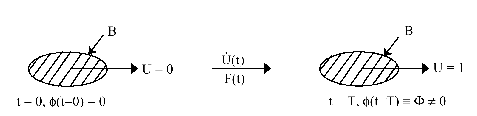
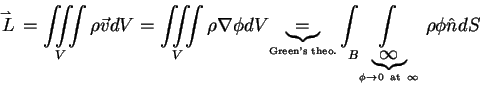
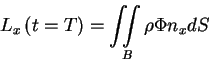
![\begin{displaymath}\int\limits_0^T {dt\left[ { - F\left( t \right)} \right]} = \...
...
{t = 0} \right) = \int\!\!\!\int\limits_B {\rho \Phi n_x dS}
\end{displaymath}](img11.gif)