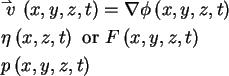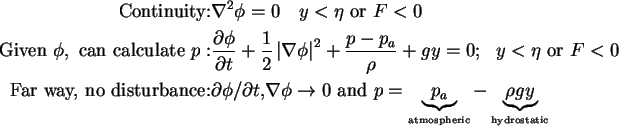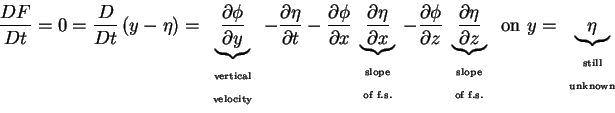Next: Linearized (Airy) Wave Theory
Up: Water Waves
Previous: Water Waves
assuming potential theory
Unknown variables:
Field equation:
Boundary Conditions:
- 1.
- On an impervious boundary
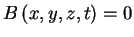 ,
we have KBC:
,
we have KBC:
Alternatively: a particle P on 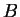 remains on
remains on 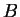 ,
i.e.
,
i.e.
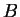 is a material surface; e.g. if P is on
is a material surface; e.g. if P is on 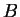 at
at 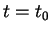 ,
i.e.
,
i.e.
so that, following P, 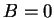 .
.
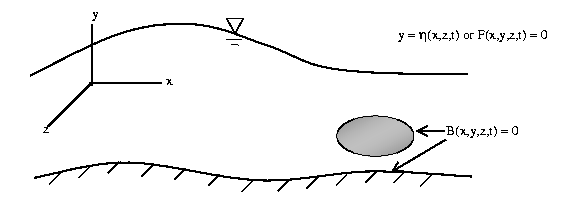
For example, flat bottom at 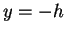 :
:
- 2.
- On the free surface,
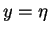 or
or
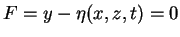 .
.
KBC: free surface is a material surface, no
perpendicular relative velocity to free surface, particle on free
surface remains on free surface:
DBC: 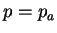 on
on 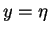 or
or 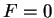 .
Apply
Bernoulli equation at
.
Apply
Bernoulli equation at 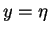 :
: