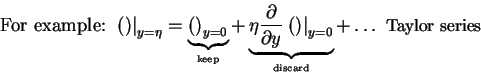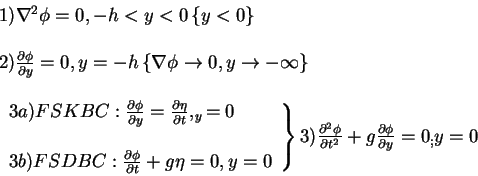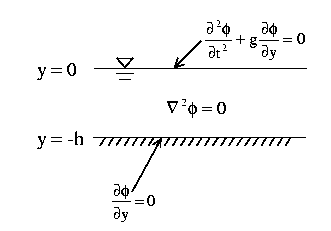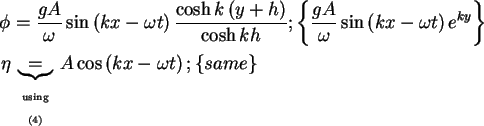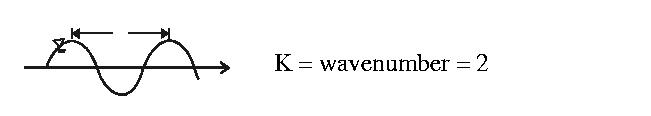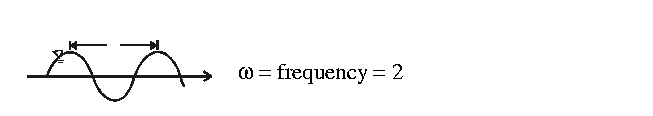Next: Dispersion Relationship
Up: Water Waves
Previous: Exact (nonlinear) governing equations
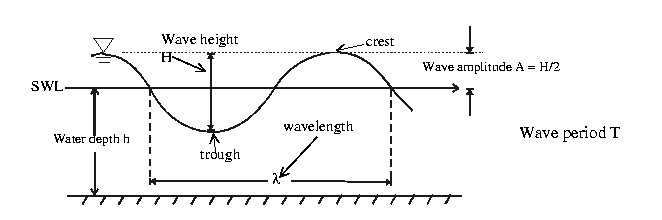
Consider small amplitude waves: (small free
surface slope)
Assume amplitude small compared to wavelength, i.e.,
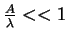 . Consequently:
. Consequently:
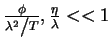 ,
and we keep only linear terms in
,
and we keep only linear terms in 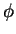 ,
,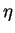 :
:
Finally:
Linear (Airy) Waves in constant finite
depth 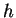 {infinite depth}
{infinite depth}
Given 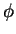 :
:
Solution of 2D Periodic Plane Progressive
Waves (using separation of variables)
Math ...(solve (1), (2),
(3))
Answer:
where 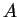 is the wave amplitude
is the wave amplitude 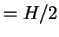 .
.
- 1.
- At
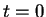 (say),
(say),
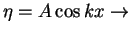 periodic in
periodic in 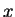 with
wavelength:
with
wavelength:
![$\lambda = 2\pi/k [L]$](img36.gif) figure
figure
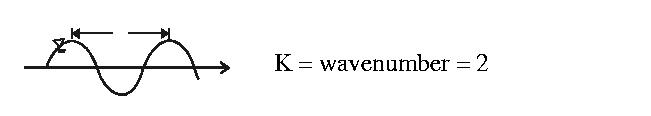
- 2.
- At
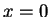 (say),
(say),
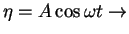 periodic in
periodic in
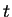 with period:
with period:
![$T = 2\pi/\omega [T]$](img41.gif) figure
figure
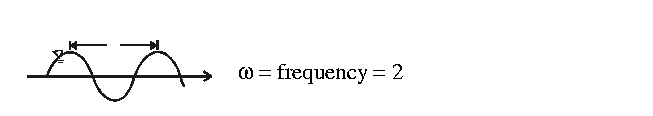
- 3.
-
![$\eta = A\cos \left[ {k\left( {x - \frac{\omega }{k}t}
\right)} \right]_ ;\frac{\omega }{k} = \left[ V \right]$](img43.gif)
Following a point with velocity
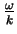 ,
i.e.
,
i.e.
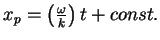 the
phase of
the
phase of 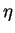 does not change:
does not change:
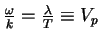 phase velocity.
phase velocity.