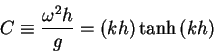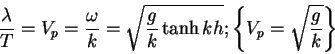Next: Solution of the Dispersion
Up: Water Waves
Previous: Linearized (Airy) Wave Theory
So far, any 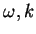 combination is allowed. Must
satisfy FSBC, substitute
combination is allowed. Must
satisfy FSBC, substitute 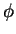 into equation (3):
into equation (3):
which gives
Given 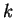 (and
(and 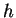 )
)
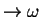 .
.
Given 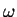 (and
(and 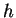 ), ...
), ...
From (6):
Dispersion Relationship (6) uniquely relates 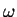 and
and 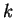 , given
, given 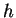 .
.
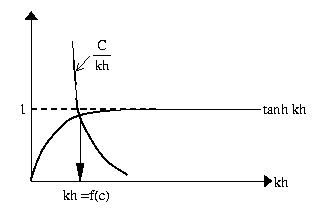
In general,
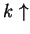 as
as
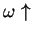 or
or
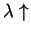 as
as
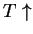 .
.
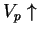 as
as
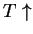 or
or
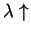 . For fixed
. For fixed 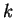 (or
(or 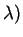 ,
,
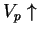 as
as
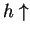 ( from shallow water)
( from shallow water)