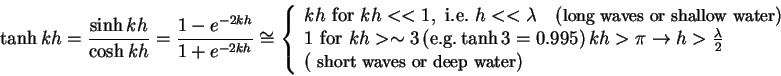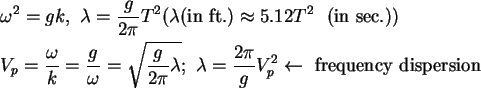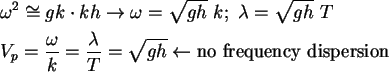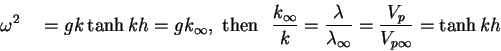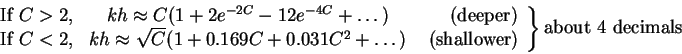Next: Characteristics of a Plane
Up: Dispersion Relationship
Previous: Dispersion Relationship
Property of 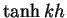 :
:
- 1.
- Deep water or short waves,
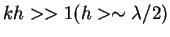
- 2.
- Shallow water or long waves,
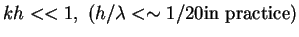
- 3.
- Intermediate depth or wavelength. Need to solve
given
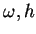 for
for 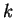 (given
(given 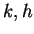 for
for 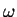 -
easy!)
-
easy!)
- (a)
- Use tables or graphs (e.g. JNN fig. 6.3)
- (b)
- Use numerical approximation (hand calculator)
- i.
- calculate
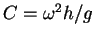 .
.
- ii.
-