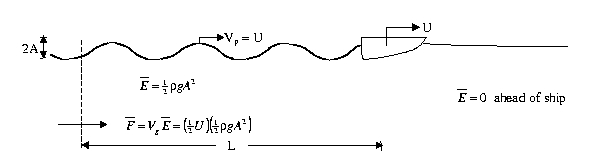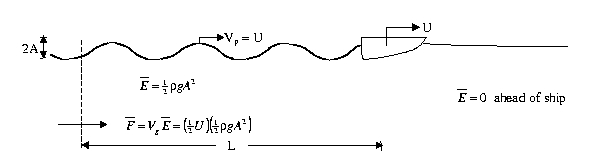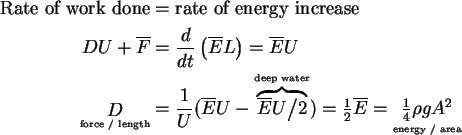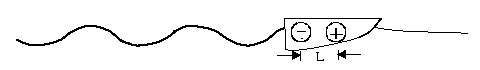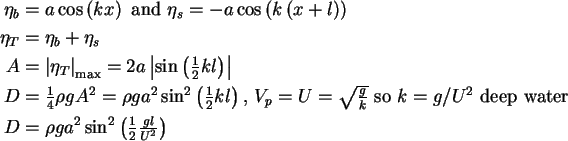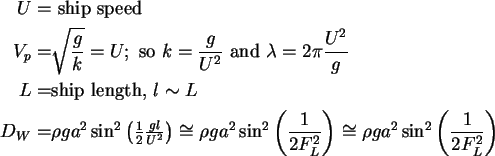Up: Free-surface waves: linear superposition,
Previous: Conservation of energy equation
Wave resistance drag on ship  .
.
Question: Amplitude A = ? (depends on U, geometry)
Superimpose a bow wave (
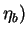 and a stern wave
(
and a stern wave
(
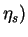 :
:
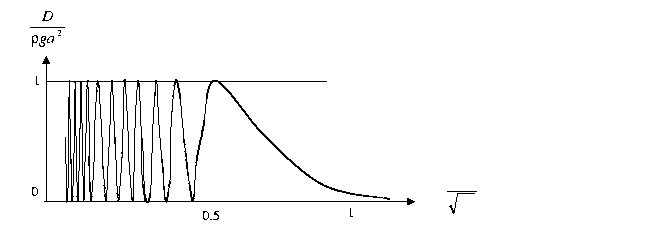
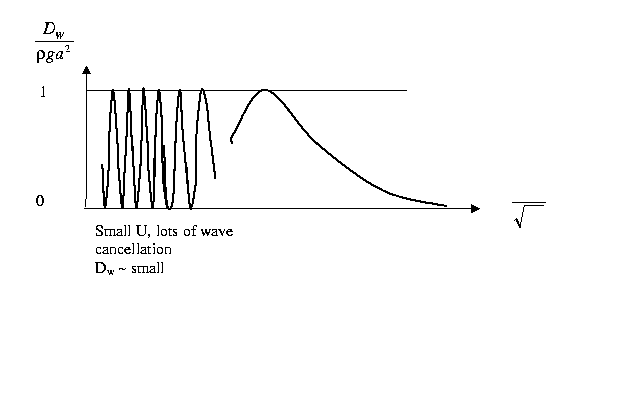
Steady ship waves (deep water)
Keyword Search