
| Vol.
XXX No.
4 March / April 2018 |
| contents |
| Printable Version |
Teach Talk
MIT Students and Deep Learning:
Perspectives and Suggestions
Abstract
In the September/October 2017 MIT Faculty Newsletter, Freeman et. al. (“How Deeply Are Our Students Learning?”) exhibit a number of apparently straightforward (to professors) problems that befuddle the vast majority of students who are doing well in the course that teaches the skills necessary to do that problem. This is taken as evidence that our teaching imparts the ability “to run the model” without imparting “deep learning.” My research group (RELATE.mit.edu) has found some additional troubling student difficulties including failing to check “solutions” for obvious flaws, starting problems without either a conceptual analysis or a coherent plan, and worsening attitudes towards learning science after taking 8.01 (Physics I). The main thrust of this article is that the education research literature provides many important insights into these – and that improving our educational outcomes forces us to bring this research (and research-developed instruments) to bear on these problems. In particular, literature on expert-novice differences, modeling-based pedagogy, and students’ epistemological approaches. Additionally, we urge departments to adopt standard MIT engineering design to reforming subjects in which learning outcomes and methods of assessing them are agreed upon first, and relevant contemporary knowledge is applied to reach the desired outcomes.
Introduction
The September/October 2017 FNL article contains a strong indictment of the results of our instructional process by a group of MIT teachers who are widely respected for their thoughtful devotion to educating MIT students: Dennis Freeman, Sanjoy Mahajan, Warren Hoburg, David Darmofal, Woodie Flowers, Gerald Sussman, and Sanjay Sarma (hereafter Freeman et. al.). They supply clear evidence that our students (and those at other top universities) have gaping holes in their “deep understanding.” They cannot “use Newton’s laws . . . to model the world,” and are unskilled at “making the model and interpreting the results.” What they are good at is “manipulation without understanding” and “running the model.”
Additional Troubling Deficiencies
Freeman et. al. is a description of multiple observed student deficiencies, but does not offer perspectives (e.g., from the education literature) that might illuminate the diagnosed difficulties, nor does it suggest how we might change our pedagogy so that students obtain deeper learning of skills and habits of mind that would enable them to overcome the aforementioned difficulties. I take these omissions as an invitation to respond to their article. Before sharing some perspectives on these student difficulties, let me first add some additional difficulties discovered by my group’s (RELATE.mit.edu) research on teaching introductory Newtonian mechanics: 8.01, 8.011, 8.01L, and a three-week Mechanics ReView taught over IAP to 8.01 students receiving a D that offers an opportunity to move on to 8.02 rather than repeat all of 8.01.
Student Attitudes About Learning Science
It is important to realize that students learning 8.01, 18.01, 6.002, etc. are young adults who have already developed both knowledge about many GIR subjects and personal beliefs about what constitutes learning them. Several Physics Education Research (PER) groups have addressed the problem of determining students’ personal epistemologies by constructing surveys that “measure student beliefs about physics and about learning physics” – quoting from the abstract of the latest such survey, the Colorado Learning Attitudes about Learning Science Survey [CLASS, (Adams et. al., 2006)]. The CLASS probes beliefs about personal enjoyment of the subject, perceptions of relevance of the subject to the world, and especially the conceptual thinking and self-confidence of students with respect to solving problems. Students are deemed more expert-like if they agree with statements similar to these:
- Physics comes from a few principles.
- When studying physics, I relate the important information to what I already know rather than just memorizing it the way it is presented.
- I am not satisfied until I understand why something works the way it does.
- I enjoy solving physics problems.
And disagree with these:
- After I study a topic in physics and feel that I understand it, I have difficulty solving problems on the same topic.
- If I don’t remember a particular equation needed to solve a problem on an exam, there’s nothing much I can do (legally!) to come up with it.
- A significant problem in learning physics is being able to memorize all the information I need to know.
The last time (2004) the CLASS was administered in 8.01 TEAL it revealed a ~ 7% decrease in learning expertise from pre- to post-survey that extended across all eight categories that CLASS probes. Faint comfort might arise because typical introductory physics courses in the U.S. lower the expertness of learning attitudes ~ 10% across these categories. Of particular concern is our additional finding for the D and F students in this class: their problem-solving self-confidence after taking this course was down ~ 30% (in all other categories their responses were indistinguishable from the ABC students).
I find this personally distressing: Newtonian Mechanics was the first science where mathematics was used to model the world based on a few fundamental assumptions – the prototypical model of most science and engineering that we teach at MIT; it is also the foundational science for several MIT majors. To teach our students that it is a pile of formulae unrelated to their world, their interest, and their future is a pedagogical travesty.
Algebra First vs. Planning a Solution
MIT professors want students to solve problems like an expert in that domain; often this means by starting with a solution plan based largely on conceptual reasoning. Yet 8.01 students typically start by writing an equation in which the given variables are already plugged into a fundamental equation (e.g., momentum conservation) – often remembered from a previous similar problem. To encourage this, part a) of several problems on the 8.01 final demanded written problem plansy research group found that just over half of our students couldn’t make a coherent plan (i.e., unambiguous, even if incorrect) – irrespective of whether their grade was A- or C (Barrantes & Pritchard, 2012). In individual discussions with ~ 20 of our students, all but one said they started those problems by seeking relevant formulae and solved algebraically, then went back and wrote the verbal plan (which was part a). They neither made a plan based on physical concepts, nor did they adduce physical reasons to buttress the applicability of the equations they started from. These findings demonstrate that neither high school nor MIT taught their students to make coherent plans for solving problems, nor even provided a learning environment where the “good” students learn such planning for themselves.
This serious divergence from faculty expectations stems from student vs. faculty differences in what they think the objective of answering the problem is: roughly “get the answer” vs. “understand how you got the solution” and what epistemological approaches should be used to reach this objective. Students’ tools were studied by closely observing small groups of students solving problems (Tuminaro & Redish, 2007), then cataloging the “epistemic games” they brought to bear on the problem. Their University of Maryland students used primarily six, including:
- Mapping Meaning to Mathematics: map the problem story (circumstances and givens) to mathematics.
- Mapping Mathematics to Meaning: Identify target variables, find equation relating target to given information (similar to “plug and chug”).
- Physical Mechanism Game: construct story about equations – often in terms of “phenomenological primitives” (DiSessa, 1988) such as a bigger object requires more force, more force à more velocity, gravity wins out in the end, etc.
The expert approach of “understand problem and plan solution starting from physical principles” was not observed. For example, when Mapping Meaning to Mathematics, “students often rely on their own conceptual understanding to generate this [mathematical representation] – not on fundamental physics principles” (Tuminaro & Redish, 2007).
We have made several efforts to teach students to write problem plans, including introducing “Tweet Sheets” that provide a framework for problem plans, space for ~ three lines of text and a small graphic and instruction on what constitutes a plan. Students can fill these in after doing group problems in class, then can bring them to the weekly quizzes. After the first few weeks, only about 15% of the students brought them to the quiz. When queried about this, most students said “I didn’t know what to write.” (About 10% of the students said “After I review the problem and write the tweet sheet, it is so easy to remember that I don’t need the sheet.”) My research group is still experimenting to find ways to help students learn to plan solutions. Tentatively we’ve concluded that they should have deliberate practice (Ericsson, 2009) of two important skills: first, determining which physical principles apply and why, and second, learning to decompose problems into sub-problems within which a unique subset of principles apply.
Perspectives for understanding these difficulties
The findings of Freeman et. al. together with our additions are all indications that our students lack “deep expert-like understanding”– in spite of their ability to score well on our final examinations. These findings include:
- Overreliance on the mathematical manipulations of the models they are trying to apply,
- Inability to create these models or to discover them,
- Inability to plan a solution, or even to state one retrospectively after answering correctly,
- Inability to make sense of, verify, and interpret the solution once it has been worked out, and
- Loss of self-confidence in problem-solving and decrease of perception that Newtonian mechanics is either relevant to their lives or intrinsically interesting.
Expert-Novice Studies
The novice-expert literature provides the best framework for understanding these difficulties, essentially providing a research-discovered list of “novice characteristics” that contain many items on the list above. The watershed paper in this field is Categorization and Representation of Physics Problems by Experts and Novices (Chi, Feltovich, & Glaser, 1981). This paper shows that novices categorize problems using surface features (pulley, block on inclined plane, collision, . . .) rather than according to fundamental domain principles as do experts. Thus students, when asked to classify problems on the basis of similarity of solution, classify a block sliding down a plane without friction as similar to a block on a plane with friction, rather than as similar to a mass on a pendulum (since both exemplify energy conservation – i.e., gain kinetic energy mgh after descending a height h).
Students classifying problems based on surface features need a huge mental library of solved problems to find one that’s sufficiently similar superficially to a given exam problem that the same solution principles also apply, as evidenced by our students’ increasing (on the post-test ) agreement with the novice-like question on the CLASS “If I want to apply a method used for solving one physics problem to another problem, the problems must involve very similar situations.”
Many of the 6000+ references to Chi’s paper expand the list of specific expert-novice differences: experts consider the problem conceptually and from different representations to plan their approach before starting to write equations, classify problems according to deep principles of the domain, have much more interconnected domain knowledge, and are able to retrieve and apply domain-specific models appropriately to unfamiliar problems (this is called strategic knowledge). When solving a problem, experts check that their solution process makes sense as they proceed, and importantly “make sense of” their answer using limiting cases, dimensional analysis, comparison with common sense, similarity to past problems, etc. Novices assume that manipulating the mathematical procedure for obtaining the answer will give a result that is correct without checking the result.
I would emphatically add “making sense of the answer” to the list of our students’ deficiencies. When I ask MIT freshmen how they’ll check their answer to a mechanics problem, they’ll most frequently say “I’d check the algebra.” I know that most physics faculty will acknowledge this deficiency: in our (Pritchard et. al., 2009) study What Else (besides the syllabus) Should Students Learn in Introductory Physics? sense-making was the top choice of the professors, and the second-lowest preference of the students. That’s understandable: students don’t get into good colleges by pausing on question 4 on a high stakes exam to consider ways to check the answer.
Many of my departmental colleagues express a strong desire to help undergraduate students “think like a physicist.” When pressed to be more specific about what this means, they typically say “check that what they do ‘makes sense’,” “organize their knowledge coherently,” “approach problems using concepts rather than algebra.” I suggest that “think like an expert” is a good description of the outcome that most MIT faculty really want for their students.
The list of expert qualities accords well with what we demand of students on our PhD candidacy exam. I find that classifying just one or two student responses to novel questions as novice vs. expert-like enables me to reliably predict whether the committee will pass or fail a student. The NAS study How Students Learn (Chi, Bassok, Lewis, Reimann, & Glaser, 1989)(Bransford, Brown, & Cocking, 2000) summarizes novice-expert differences and is a good place to start learning this valuable perspective.
| Back to top |
Modeling
David Hestenes (Hestenes, 1987) has convincingly argued that models form the everyday mental tools that most STEM professionals use. The word model appears 12 times in Freeman et. al. and I find it valuable in my professional and teaching life. Models and modeling are central to MIT and explicit in many upper division subjects, especially engineering: we use mathematics to make models of the structure and behavior of some well-specified system.
Yet in most GIRs, we fail to impart knowledge about models explicitly:
- None of the Science GIR subjects mention “model” – with the exception of 8.02.
- We recommend textbooks that don’t give a modeling perspective, e.g., the best-selling Young and Freedman (11th edition used in 8.01 & 8.02) mentions “model” briefly in the introduction and not again in the subsequent 1714 pages.
- We often provide “formula sheets” that list formulae without indicating what role each formula plays in which model (e.g., law of force, constraint, law by which state variables change, . . .), thereby encouraging the belief that “subject X is a pile of formulae” rather than imparting the view that the formulae are only one part of a particular model of reality in that subject.
The result is students who, at the end of introductory subjects, can manipulate the equations, i.e., “run the model” in Freeman et. al. – often without being able to name the model they are applying or knowing its limitations.
For example, in 8.01 the equations F=ma and F = mfriction* m*g are used in the same solution without knowledge of the very limited applicability of the second formula (fails for static friction, assumes that normal force is mg). Expert scientists and engineers are careful to check the applicability of the model as part of their solution process – the types of systems and circumstances under which the model containing these formulae applies, the model’s limitations, and whether its predictions make sense (NAS13).
Hestenes and collaborators have developed a pedagogy called “modeling Instruction” for physics that is explicitly designed to teach the ideas and procedures of modeling reality. In modeling instruction, students are guided to discover the basic models in laboratory, and to apply them to problems – a process called “modeling.” This pedagogy leads to very large improvements of students’ scores on both concept inventories and more problem-oriented tests; high school students start lower but finish higher than students taking traditional introductory courses at selective colleges (Hestenes, Wells, & Swackhamer, 1992). A recent review paper of ~ 50 different introductory physics courses (Madsen, McKagan, & Sayre, 2015) documents another benefit of modeling instruction: it uniformly improves the expertness of students’ learning attitudes as measured by the Colorado Learning Attitudes about Science Survey (CLASS ) – typically by ~ 11%.
Hestenes’ group started the American Modeling Teachers Association (modelinginstruction.org) that runs two-week workshops on modeling instruction which upwards of 10% of all U.S. high school physics teachers have attended, and this pedagogy is widely known among physics high school teachers. (This summer there will be a total of ~ 62 workshops for biology, chemistry, physical science, and physics teachers.) This is known by only a small percentage of college or university faculty – unfortunate because modeling pedagogy would give many MIT professors a valuable perspective on reforming their subjects.
As an example, in developing MIT’s three-week Mechanics ReView, my group has designed a modeling-based approach to categorizing domain knowledge and problem solving, and found that in addition to improving grades on the final exam by ~ 1.5 grades it improved their expert-thinking by ~ 11% as measured by CLASS. Importantly, these students also showed an improvement in their subsequent 8.02 performance relative to their peers who either did not take the ReView or who took another full semester of traditionally taught 8.01 (A. Pawl, Barrantes, & Pritchard, 2009; Rayyan, Pawl, Barrantes, Teodorescu, & Pritchard, 2010).
Cognitive
The MIT course catalog is based on a list of topics that are taught in each subject. A complementary perspective is to specify the cognitive skills that the student is supposed to learn. Indeed, a cognitive perspective is highly germane to understanding the student difficulties mentioned above. The figure below shows a cognitive hierarchy, and gives the teacher’s relationship with questions at each cognitive level (below).
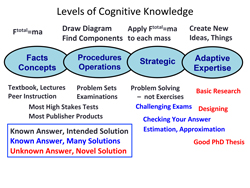
(click on image to enlarge)
The figure divides cognitive knowledge into four categories, shown as overlapping ovals with examples from Newtonian mechanics at the top. These start on the left with a foundation of facts, definitions, and simple concepts like how to define and measure acceleration. Built on this factual foundation (expressed by its oval overlapping) is knowledge of procedures and operations – these are the models. Confronted with an unfamiliar problem, an expert applies strategic knowledge to sort through the known procedures (models) to determine which might be relevant or helpful, then solves the problems using the relevant model(s). At the very right is Adaptive Expertise, the knowledge/ability to create something new. These categories are closely paralleled by cognitive taxonomies like those of Bloom and Marzano (Marzano & Kendall, 2007; Teodorescu, Bennhold, Feldman, & Medsker, 2013).
This perspective illuminates typical tasks assigned by teachers; these are presented (below the ovals) in different colors depending on whether the problem/task has a known answer, and whether the teacher who poses it intends the student to answer it in a particular way. Let’s categorize our current instructional approach (e.g., in 8.01) through this lens: list the topics in the syllabus, teach this material (mostly concepts and procedures) in serial order (energy one week, momentum the next, angular momentum later, . . .), and give lots of practice (homework) each week, concentrating on the topic of the week. Obviously, this pedagogy is focused on the two left-most ovals (facts and procedures). Such instruction doesn’t improve students’ strategic knowledge because they don’t need to learn how to determine whether momentum is a key to this problem when momentum is this week’s topic.
The facts & procedures-based instructional approach allows little opportunity for helping the students obtain strategic knowledge spanning the whole range of topics in that subject – the ability to organize their knowledge of different facts and procedures so that it can be fluently accessed when confronting an unfamiliar problem. Indeed, in my bookshelf of introductory physics textbooks, not one attempts explicitly to instill strategic knowledge, for example with a chapter whose title is something like “How to analyze a new problem to determine which of the previous 12 chapters can help you solve it.” It is not surprising that unfamiliar final exam problems involving several of the studied procedures are considered to be very difficult by our students. Many of the problems in Freeman et. al. don’t have a clear similarity to any of the weekly homework problems in the subject; hence they expose the students’ lack of strategic knowledge.
Other Helpful Perspectives
Several other useful (to me) perspectives are Kahneman’s Type 1 and Type 2 thinking (quick and reactive vs. thoughtful and logical) and its relevance to short concept questions vs. traditional long-form problems, the importance of quick association among relevant domain vocabulary as a measure of knowledge interconnectedness (Gerace, 2001), and defining “understand a concept” as “fluency with, and interrelating of, the representations commonly used with that concept.” (e.g., Motion with constant acceleration might be represented with a table of position vs. time, a formula for velocity vs. time, a strobe picture, or a graph of velocity vs. position.)
| Back to top |
Addressing These Deficiencies
Having broadened the list of troubling student deficiencies and offered some perspectives, I now turn to how individual departments can reform our subjects to help students overcome these difficulties.
Outcomes and Goals
Freeman et. al. and I are distressed that, having done well in our subjects, our students are not reaching the learning outcomes involving skills, habits, and attitudes that many faculty strongly believe are important. I put the blame on our system (shared by other colleges) that defines a subject as a syllabus of topics and subtopics that will be taught by an expert in that subject. This teacher-centered description lacks any specification of what is expected of students in terms of skills, habits, or abilities. Thus addressing these deficiencies starts with:
#1 Departments must specify subjects in terms of outcomes expected of students – both learning outcomes with respect to specific topics, and general skills.
Thus, where the current course description lists a topic, e.g., “momentum,” there would be a learning objective “identify when momentum is/is not conserved.” This has the advantage that a professor can write a problem that most other department members would agree assesses a particular learning objective. Importantly, learning objectives can address more general learning outcomes than topics – for example “learn to check their solutions using dimensions and limiting cases.” Specifying learning objectives would enable us to emphasize general skills and habits that are generally considered important in the 21st century such as the 4 C’s - collaboration, communication, critical thinking and problem solving, and creativity (p21.org, (NGSS Lead States, 2013)).
I also recommend that we move our instructional goals toward Strategic and Creative cognitive levels because smart phones and Internet search engines provide instant access to facts and integrated collections of procedures (like Wolfram alpha, the computational package r, Mathematica, etc.).
For example, we can remove “challenging” algebra-intensive problems the first time students are exposed to a topic, and add review problems later that explicitly require students to say which previously studied topics apply in a given physical situation and why – or give problems with multiple choice answers where the distractors can be eliminated by dimensional analysis or special cases. Given that freshmen will forget over half of what they learn but don’t use regularly by graduation (Ebbinghaus, Ruger, & Bussenius, 1913; Andrew Pawl, Barrantes, Pritchard, & Mitchell, 2010), but will improve on skills that they reuse, answer checking, dimensional analysis, and determining what’s conserved should receive more emphasis than they do now – especially when reforming subjects like GIRs where most students will major in another course.
Assessment
Given that the department has set the learning objectives and goals, it is important to realize that assessment sets the standard for student learning (and has strong influence on the instruction). So,
#2 Departments must adopt assessment instruments and develop calibrated question pools that accurately assess their learning goals.
This process should strongly consider incorporating some of the research-developed instruments. Examples might include instruments that evaluate students’ ability to reason from fundamental physical principles (Andrew Pawl et. al., 2012), assessments of general scientific reasoning (Lawson, 1978), and widely used instruments whose typical results are known for different institutions, e.g., the CLASS, Test of Understanding of Graphs (TUG), and discipline-based instruments like the venerable Force Concept Inventory that has transformed teachers’ views on the importance of conceptual reasoning. We should also consider making some instruments of our own – a good place to start would be to collect questions like those in Freeman et. al. This process will result in stable year-to-year assessments of student knowledge and learning. As a side benefit, these assessments can complement student evaluations of learning in assessing teacher performance.
DBER – Discipline-Based Education Research
The main thrust of this article is that the education research and cognitive science literature provides many important insights and remedies that address the serious student deficiencies identified by Freeman et. al. and in this article – and that improving the outcomes of our subjects forces us to bring this research (and research-developed assessment instruments) to bear on our efforts to improve our courses. This is a tremendous challenge due to the immensity of the possibly relevant literature. To put this in perspective, a typical faculty member is well acquainted with literature in a specialty like Atomic Physics Research for which a Google search will have ~ 0.1M hits, in comparison Physics Research will yield ~ 2.7M, and Education Research ~ 12.4M, a count that probably excludes much education-relevant research from fields like cognitive science, behavioral psychology, etc. Hence it is unrealistic to expect even our most dedicated professors to know the literature relevant to education – even the dedicated teacher-authors in Freeman et. al. believe that “researchers in STEM education [have not] . . . identified these problems and shown their solution.” I believe that the only realistic route to filtering through the voluminous education research to get beyond the “educational technology fix of the day” and to find what will truly help us improve our subjects is that:
#3 We must incorporate Discipline-Based Education Researchers into processes #1 and #2 above, as suggested in the recent National Research Study, (Singer, Nielsen, & Schweingruber, 2012).
Summary
The above three recommendations – set goals, agree on how to assess them, and incorporate relevant educational research – are consistently recommended by education reformers, and have been successfully implemented at two selective universities by Nobel prizewinner Carl Wieman (Wieman, 2017). Grant Wiggins has advocated them, calling the process “backward design” to contrast it with the topics first/assessment last approach that is typical in universities (Mctighe & Wiggins, 2012).
It should be easy for MIT faculty to adopt backward design because it is really the “forward design” that we practice in our professional lives: select goals, determine how we’ll measure them, build on relevant literature, experiment /fail/recycle until the goals are met, then publish or patent. Hopefully, we can adopt this familiar practice to systematically and scientifically improve MIT undergraduate education.
I acknowledge helpful comments by Lori Breslow, Sanjoy Mahajan, Leigh Royden, and Gerald Sussman.
I welcome comments on this (dpritch@mit.edu) and encourage further Faculty Newsletter articles on improving MIT education.
| Back to top |
References
Adams, W., Perkins, K., Podolefsky, N., Dubson, M., Finkelstein, N., & Wieman, C. (2006). New instrument for measuring student beliefs about physics and learning physics: The Colorado Learning Attitudes about Science Survey. Physical Review Special Topics - Physics Education Research, 2(1), 10101. http://doi.org/10.1103/PhysRevSTPER.2.010101
Barrantes, A., & Pritchard, D. (2012). Partial Credit Grading Rewards Partial Understanding. (unpublished – ask me for a copy)
Bransford, J. D., Brown, A. L., & Cocking, R. R. (2000). How people learn: Brain, mind, experience, and school: Expanded edition. Washington, DC: National …. Washington, D.C.: National Academy Press. Retrieved from http://www.eric.ed.gov/ERICWebPortal/recordDetail?accno=EJ652656
Chi, M. T. H., Bassok, M., Lewis, M. W., Reimann, P., & Glaser, R. (1989). How Students Study and Use Examples in Learning to Solve Problems, Cognitive Science, 182, 145–182.
Chi, M. T. H., Feltovich, P. J., & Glaser, R. (1981). Categorization and representation of physics problems by experts and novices. Cognitive Science, 5, 121–152. Retrieved from http://www.sciencedirect.com/science/article/pii/S0364021381800298
DiSessa, A. (1988). diS88 diSessa Phenomenological Primitives “knowledge in pieces”.pdf. In P. Forman, G. Pufall (Ed.), (p. 49).
Ebbinghaus, H., Ruger, H. A., & Bussenius, C. E. (1913). Memory: A contribution to experimental psychology., 1913. http://doi.org/10.1037/10011-000
Ericsson, K. A. (2009). Discovering deliberate practice activities that overcome plateaus and limits on improvement of performance. In A.Willamon, S.Pretty, & R.Buck (Eds.), Proceedings of the International Symposium on Performance Science (pp. 11–21). Utrecht, The Netherlands: Association Europienne des Conservatoires Academies de Musique et Musikhochschulen (AEC).
Gerace, W. J. (2001). Problem Solving and Conceptual Understanding. Proceedings of the 2001 Physics Education Research Conference, 2–5.
Hestenes, D. (1987). Toward a modeling theory of physics instruction. American Journal of Physics, 55(5), 440. Retrieved from http://scitation.aip.org/content/aapt/journal/ajp/55/5/10.1119/1.15129
Hestenes, D., Wells, M., & Swackhamer, G. (1992). Force concept inventory. The Physics Teacher, 30(3), 141. http://doi.org/10.1119/1.2343497
Lawson, A. E. (1978). The development and validation of a classroom test of formal reasoning. Journal of Research in Science Teaching, 15(1), 11–24. http://doi.org/10.1002/tea.3660150103
Madsen, A., McKagan, S. B., & Sayre, E. C. (2015). How physics instruction impacts students’ beliefs about learning physics: A meta-analysis of 24 studies. Physical Review Special Topics - Physics Education Research, 11(1), 1–19. http://doi.org/10.1103/PhysRevSTPER.11.010115
Marzano, R., & Kendall, J. (2007). The new taxonomy of educational objectives (2nd ed.). Thousand Oaks, CA: Corwin Press.
NGSS Lead States. (2013). Next Generation Science Standards: For States, By States. Washington, D.C.: The National Academies Press.
Pawl, A., Barrantes, A., Cardamone, C., Rayyan, S., Pritchard, D. E., Rebello, N. S., . . .Singh, C. (2012). Development of a mechanics reasoning inventory. In 2011 Physics Education Research Conference (Vol. 2, pp. 287–290). http://doi.org/10.1063/1.3680051
Pawl, A., Barrantes, A., & Pritchard, D. E. (2009). Modeling applied to problem solving. In AIP Conference Proceedings (Vol. 1179). http://doi.org/10.1063/1.3266752
Pawl, A., Barrantes, A., Pritchard, D. E., & Mitchell, R. (2010). What do Seniors Remember from Freshman Physics??
Pritchard, D. E., Barrantes, A., Belland, B. R., Sabella, M., Henderson, C., & Singh, C. (2009). What Else (Besides the Syllabus) Should Students Learn in Introductory Physics? In 2009 Physics Education Research Conference (pp. 43–46). http://doi.org/10.1063/1.3266749
Rayyan, S., Pawl, A., Barrantes, A., Teodorescu, R., & Pritchard, D. E. (2010). Improved student performance in electricity and magnetism following prior MAPS instruction in mechanics. In AIP Conference Proceedings (Vol. 1289). http://doi.org/10.1063/1.3515221
Singer, S. R., Nielsen, N. R., & Schweingruber, H. A. (2012). Discipline-Based Education Research: Understanding and Improving Learning in Undergraduate Science and Engineering. ( Committee on the Status, Contributions, and Future Directions of Discipline-Based Education Research; Board on Science Education; Division of Behavioral and Social Sciences, and Education, Eds.). The National Academies Press. Retrieved from https://www.nap.edu/catalog/13362/discipline-based-education-research-understanding-and-improving-learning-in-undergraduate
Teodorescu, R. E., Bennhold, C., Feldman, G., & Medsker, L. (2013). New approach to analyzing physics problems: A Taxonomy of Introductory Physics Problems. Physical Review Special Topics - Physics Education Research, 9(1), 10103. http://doi.org/10.1103/PhysRevSTPER.9.010103
Tuminaro, J., & Redish, E. F. (2007). Elements of a cognitive model of physics problem solving: Epistemic games, (January), 1–22. https://journals.aps.org/prper/abstract/10.1103/PhysRevSTPER.3.020101
Wieman, C. E. (2017). Improving How Universities Teach Science.
| Back to top | |
| Send your comments |
| home this issue archives editorial board contact us faculty website |