Cylinder-Plate geometry

H.B.G. Casimir and D. Polder, Phys. Rev. 73, 360 (1948)

"The Influence of Retardation on the London-van der Waals Forces"

For asymptotically large separations H, the attractive force between a sphere (radius R) and a plate is

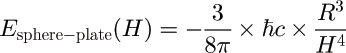
Sukenik, Boshier, Cho, Sandoghdar, and Hinds, Phys. Rev. Lett. 70, 560 (1993)

"Measurement of the Casimir-Polder force"

from deflection of sodium atoms passing through a cavity.

What is the force between a metallic cylinder (wire) and a plate?

 Analogy with parallel plates suggests an energy proportional to area:

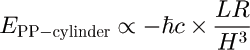
 Analogy with the Casimir-Polder results suggests (in the limit R << H ):

 Proximity force approximation (exact in the limit R >> H ) gives:

 We find the following exact results (in the limit R >> H ):

due to long wave-length charge fluctuations along the length of the cylinder.

  Emig,   Jaffe,  Kardar, & Scardicchio, Phys. Rev. Lett. 96, 080403 (2006).

Unexpected non-monotonicity due to three-body effects:

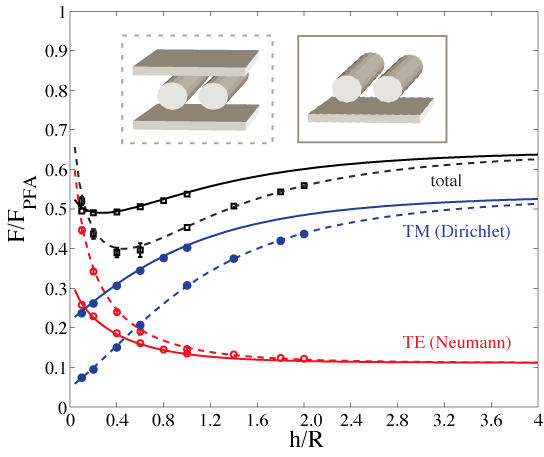
"Nonmonotonic effects of parallel sidewalls on Casimir forces between cylinders,"

Rahi, Rodriguez, Emig, Jaffe, Johnson,  & Kardar, Phys. Rev. A 77, 030101(R) (2008)