REMAKING THE NEURAL NET: A PERCEPTRON LOGIC UNIT. M. Van Alstyne.
Independent Project; MIT Lincoln Laboratory; Rm M209D; Box 73; Lexington,
MA 02173 USA.

A three node network to compute XOR is possible by using transcendental
functions. As the logistic function increases monotonically it cannot play
the same role as a sine in performing an intrinsically periodic operation.
While four node, hidden unit logistic solutions exist, none can achieve
a solution in three. The nonmonotonic network solution examined here, however,
learns to solve all eight binary operations and to discriminate even between
inputs 0,1 and 1,0, which the binary operators treat identically. Further,
it learns any such computation from the same initial state. In areas where
they coincide, average sine node networks require fewer than half the number
of training iterations required by logistic node networks.
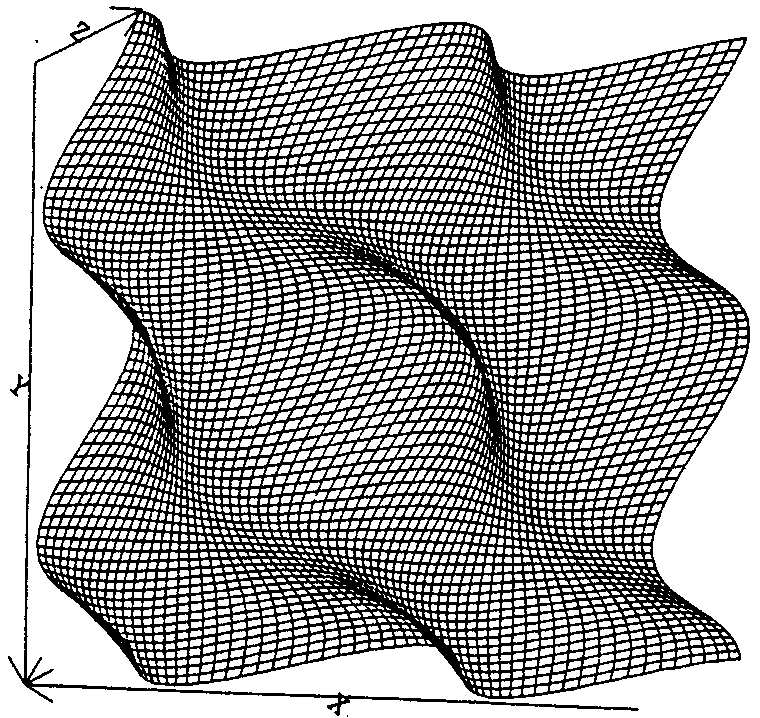
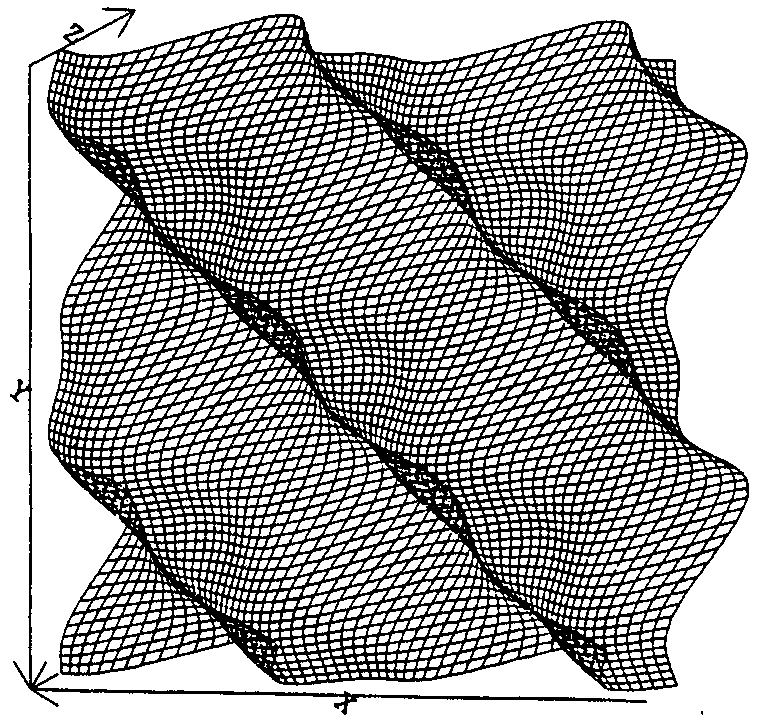
Figure 1, on the left, shows a linear error plot. Figure 2, on the right,
shows a squared error plot.
The paradigm, in achieving this uniform initial state, differs from standard
back propagation in its use of linear rather than quadratic error. A linear
error term results in a remarkably smooth error contour with an infinite
number of global minima. More interesting still, this contour is
basically the same irrespective of the operation being learned. Each binary
operation lies, under this representation, at a fairly constant distance
from other operations in error space. Learning takes place by "lifting"
and "shifting" the error contour to find an appropriate zero point
while deforming the original shape only slightly. A linear error contour
is depicted in Fig. 1 and a contrasting squared error contour is depicted
(for "AND" only) in Fig. 2.
Figure 3 gives a vector representation in spherical coordinates of solutions
to the eight binary operations. To achieve an exact solution, a resting
bias adds to the sine term bringing negative output values to zero and positive
values to one. Figure 1 shows the basic error as a function of two weights
from the input nodes with a resting bias of Pi/2. As the network learns
resting biases and connection weights this shape warps, but at a constant
bias it remains identical for all permutations on a three node network.
Figure 2 illustrates a second advantage of a linear error over an quadratic
error function by showing the comparatively more complicated shape of the
quadratic.
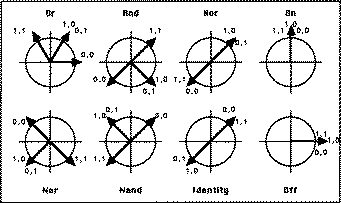
Figure 3 -- This shows vector representations of all eight logic operations.
Using a resting bias, this configuration has achieved error values as
low as le-15. A resting bias functions as a source of activation from a
node emitting a constant signal. It contributes to node output, however,
not to node input. Unlike the bias term of the logistic function, it therefore
requires a slightly modified learning rule a modest penalty for the additional
accuracy it contributes. While a sinusoidal activation function has the
biologically unusual property of periodicity, it can be restricted to one
phase by combining it with a multiplicative factor inversely proportional
to the magnitude of its connection weights.
If it can be shown that more difficult problems are similarly free of local
minima, a transcendental network would prove to be a powerful learning tool
as any continuous function may be approximated using sine waves. Simple
number, parity, and complement problems have proven tractable, and an experiment
to learn to recognize a digitized calculator display is ongoing.
References:
[1] Rumelhart, D.E., Hinton, G.E., and Williams, R. J; "Learning Internal
Representations by Error Propagation;" Parallel Distributed Processing,
Vol. I; ed. Rumelhart, D.E. and McClelland, J.L.; MIT Press, Cambridge,
MA.; 1986.
[2] Minsky M.L., and Papert, S.; Perceptrons, Expanded Edition; MIT Press,
Cambridge, MA. 1988.
[3] Burr, D.J.; "A Neural Network Digit Recognizer," Proc. IEEE,
International Conference on Systems, Man, and Cybernetics; October, 1986.
[4] Dym, H., and McKean, H.P. Fourier Series and Integrals; Academic Press,
New York; 1972.
