Patient Diagnoses
Diagnosing
Schizophrenia via CAT Scans
Out of 1000 random people:
15 are schizophrenic
985 are not
In a CAT scan, 30% of schizophrenics show atrophy (shrinkage) of
the brain. 30% of 15 = ~5
2% of nonschizophrenics show similar atrophy. 2% of 985 = ~20
Out of a total of 25 cases of brain atrophy in 1000 random people,
only one-fifth arise from schizophrenics.
Explanation: In making this determination, we must consider *both*
the higher rate of atrophy in schizophrenics *and* the rarity of
schizophrenia in the general population.
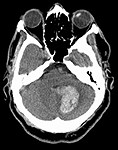
However, Hinckley was subjected to a CAT scan because he was already
suspected of being schizophrenic. The above calculation is only
true for a completely random sampling of people.
Text from Chapter:
In March 1981, John Hinckley shot President Reagan in an attempt
to assassinate him. At the subsequent trial, no one denied that
Hinckley had fired the shots that had wounded four people; the point
of contention was whether he was sane when he did so.
His lawyers asserted
that he was insane because he suffered from schizophrenia. To buttress
their case, they sought to introduce into evidence a CAT-scan of
Hinckley's brain that revealed it to be atrophied. Because such
atrophy is believed to be present in 30% of schizophrenics but only
2% of others, the attorneys depicted the test result as a powerful
indicator of Hinckley's deranged condition.
At least one mathematician
has suggested, however, that this argument represented a dreadful
abuse of statistics. The criticism--which takes note of official
estimates that 1.5% of Americans are schizophrenic--centers on the
answer to the question: if a randomly chosen American takes a CAT-scan
and it shows brain atrophy, what is the probability that he is schizophrenic?
Let us focus now on this question.
We define several events:
S: a randomly-chosen
participant in a national CAT-scan suffers from schizophrenia
S*: the complementary
event that this participant is not schizophrenic
A: the participant's
CAT-scan shows brain atrophy
In this notation, the mathematician's question above reduces to
a call for the calculation of P(S|A). The numbers available for
such an endeavor are:
P(S) = .015; P(S*) =1-.015 = .985; P(A|S)= .30; P(A|S) = .02.
Solution
From Bayes' Theorem, we know that
P(S A) = P(S) P(A|S)/
P(A) (14)
Given the numbers in the preceding paragraph, we already know that
P(S) = .015 and P(A|S) = .30. But P(A), the denominator of (14),
requires some further work. We first "break down" the
event A to
write:
P(A) = P(S and A) + P(S* and A) (15)
To understand (15), observe that A can occur in two ways: the
person chosen for the scan is schizophrenic and shows brain
atrophy (S and A), or the person chosen is not schizophrenic but
still shows atrophy (S* and A). Because these two possibilities
are mutually exclusive, (14) arises in consequence of the second
probability law.
Now we can twice employ
(IVB) to restate (15) as:
P(A) = P(S*)P(A|S*) + P(S)P(A|S)
and hence (14) as:
P(S A) = P(S) P(A
S)/[P(S) P(A S) + P(S*) P(A S*)
Because P(S)=.015, P(S*)
=.985 and P(A|S*) = .02, we
can write P(S A) = .186. In short, the person has better than a
4 in 5 chance of not being schizophrenic.
A relative frequency argument amplifies on the result. Out of every
1000 people tested, roughly 15 will be schizophrenic and the other
985 not so. On average, about 30% of the schizophrenics (i.e. about
15*.3, or about five) will show atrophy, as will 2% of the nonschizophrenics
(i.e. about 985*.02, or about 20). Thus, of the roughly 25 cases
of atrophy arising from these 1000 people, only about one-fifth
(5/25) arise from schizophrenics. What happens is that 2% of a large
number (985) dwarfs 30% of a small one (15).
The mathematician's concern was that Hinckley's lawyers were emphasizing
the higher rate of atrophy among schizophrenics
(30% vs. 2%) but ignoring the rarity of schizophrenia in the population.
Their evidence, he believed, would make it hard for jurors to recognize
that the CAT-scan finding in itself was a dubious signal of schizophrenia.
Discussion
The mathematician's argument is intriguing, and it suggests the
value of probabilistic thinking in preventing the neglect of important
information. One can, however, imagine another interpretation of
the numbers more favorable to the defendant. Even though our primary
interest is in statistics rather than criminal law, a brief statement
of an alternative viewpoint seems useful.
The Bayesian computation
makes clear that, among Americans chosen at random for CAT-scans,
only about one-fifth of those who showed brain atrophy would actually
be schizophrenic. But Hinckley's CAT-scan was not part of some national
sample; it was performed precisely because he was suspected of schizophrenia.
Given that circumstance, should Hinckley be assigned the same prior
probability of suffering the malady (1.5 percent) as a hypothetical
member of the population?
To consider another
perspective, suppose that a juror, after hearing psychiatric testimony
and other evidence, believes the probability is P that Hinckley
is schizophrenic. (P corresponds to the .015 in the national calculation.)
On learning the CAT-scan results, she should revise that probability
via Bayes' Theorem to the value Q that follows:
Q = .3P/ (.3P +.02(1-P)
(16)
When (16) is used to modify various values of P, the results are
most interesting. For P=.5 (which corresponds to the case of complete
indecision), Q takes on the far less equivocal value of .94. When
P=.75, Q=.98. And even when P is only 1/4, Q takes on the immensely
higher value of 5/6.
It appears, therefore,
that the CAT-scan results, even if not decisive in their own right,
could be potent in conjunction with the other elements of the case
(which have already raised P above the population average of .015).
. And this general situation is not unusual: often a strong case
consists of an accumulation of clues that, considered singly, would
not be compelling.
|

