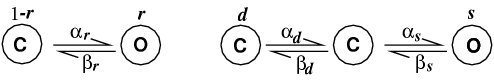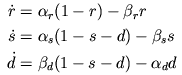A NEURON Programming Tutorial - part D
Introduction
Although our simulated neurons were given a characteristic
subthalamic nucleus projection neuron morphology in tutorial part C, they still only contain the
default Hodgkin and Huxley types of sodium and potassium ion
selective channels. We would like to make our neurons much more
electrophysiologically characteristic of subthalamic
nucleus neurons. There are many channel types we would want to
add, but for the tutorial we will add only one new type.
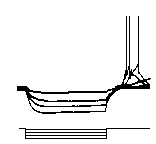 An important
electrophysiological feature of subthalamic neurons is the post
hyperpolarising response. When a neuron is hyperpolarised (e.g.
by current injection or inhibitory synaptic input), at the end
of the hyperpolarisation, a burst of activity is observed in
subthalamic projection neurons (see left). This response is
mediated by a low threshold calcium selective ion channel,
called the T-type calcium channel.
An important
electrophysiological feature of subthalamic neurons is the post
hyperpolarising response. When a neuron is hyperpolarised (e.g.
by current injection or inhibitory synaptic input), at the end
of the hyperpolarisation, a burst of activity is observed in
subthalamic projection neurons (see left). This response is
mediated by a low threshold calcium selective ion channel,
called the T-type calcium channel.
The current IT produced from the
T-type calcium channels was characterised within the
Hodgkin-Huxley framework by Wang et al. (1991):
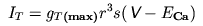
where gT(max) is the
maximum T-type calcium conductance, r is the
activation state variable, s is the
inactivation state variable, ECa is
the reversal potential for calcium and V is the
neuron membrane potential. The state variables
r and s are given by the
following kinetic systems:
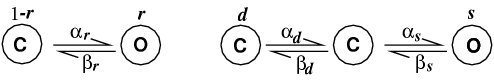
Here "C" refers to a closed state and "O" refers to an open
state. The α and β variables are the forward and
backward rate constants from one state to another; they are
voltage dependent functions specified in Wang et al.
(1991). Note that inactivation is a three state kinetic
process, with fast (s) and slow
(d) components).
The kinetic schemes translate to three differential
equations:
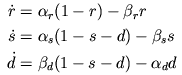
We would like to add this channel to our model. Sadly this
cannot be done with the programming language hoc that we have used in the previous tutorial
parts. Instead we have to learn the Model Description
Language (NMODL) provided for defining
additional distributed membrane mechanisms such as ion channels
and calcium pumps and point processes such as synapses. [Note,
in the future it is planned that NMODL
descriptions will be replaced by JAVA objects].
This tutorial shows you how to use NMODL
to create the T-type channel we need. This should be applicable
to other types of voltage-dependent channels too. NMODL is capable of much more, but that is outside
the scope of this tutorial; the document Expanding
NEURON's Repertoire of Mechanisms with NMODL by Mike
Hines and Ted Carnevale contains comprehensive description of
how to use NMDOL for different purposes. A shorter version of
this document is also available
(Hines & Carnevale, 2000).
NMODL and NEURON
A membrane mechanism description using NMODL is laid out in a text file. The NEURON interpreter cannot read this file directly as
it can with hoc files. Instead, the NMODL file has to be compiled into a
form that NEURON can use. Suppose that we
have created a file CaT.mod containing our
description of the T-type calcium channel in NMODL. How you incorporate this new mechanism into
NEURON depends on what operating system you
are using.
- UNIX or LINUX users:
-
UNIX and LINUX users should just change to the directory
that contains the CaT.mod file, and there type
the command
nrnivmodl
at the operating system prompt. Under Linux on a PC with an
Intel-compatible CPU, this creates a new NEURON executable called i386/special (the i386
subdirectory will be created automatically if it does not
already exist) whose library of mechanisms includes our T
current. To launch this new executable and have it load
your model file, just type
nrngui sthD.hoc
at the OS prompt in the directory that contains i386.
sthD.hoc is the file that contains our model
specification, and it is nearly identical to
sthC3.hoc from tutorial part C.
- MSWin users:
-
MSWin users should just launch
Start / Programs / Neuron / mknrndll
This brings up a directory browser that can be used to
navigate to the directory that contains the
CaT.mod file. When you get to the proper
directory, click on the button labelled "Make nrnmech.dll".
This compiles all the mod files in this directory and
creates a file called nrnmech.dll that contains the new
compiled mechanisms. nrnmech.dll will be automatically
loaded when you double click on a hoc
file in this directory.
- MacOS users:
- MacOS users only need to drag the directory that contains
CaT.mod and drop it onto the mknrndll icon. This
produces a nrnmech.dll file that is automatically loaded when
you double click on any hoc file in the
same directory.
Note, sthD.hoc differs from sthC3.hoc
from tutorial part C in that our soma
definition in the template now inserts our newly defined CaT
membrane mechanism:
soma {
nseg = 1
diam = 18.8
L = 18.8
Ra = 123.0
insert hh
gnabar_hh=0.25
gl_hh = .0001666
el_hh = -60.0
insert CaT
}
Why do we have to go through this cumbersome procedure every
time we want to create or modify a channel? The reason is that
membrane mechanisms are used on every time step, and therefore
need to be efficient. Converting the NMODL file to C-code and
then compiling this into a new NEURON
program or library (which is what nrnivmodl and
mknrndll do) leads to more efficient simulation.
A description of a membrane mechanism in NMODL is a text file divided into a number of
blocks. A block begins with a keyword defining the type of
block, then an open brace "{", followed by block
specific definitions, and finally, the block is ended with a
closing brace "}". The best way to learn to program new
membrane mechanisms using NMODL is by
following examples of already defined mechanisms. There are a
number of NMODL examples provided with the
NEURON package. Here we will go through,
step by step, an example of a new channel mechanism.
We will construct a NMODL file, called
CaT.mod to calculate the low threshold calcium
channel kinetics. As with hoc files we can
use our favourite text editor to create this file.
The TITLE and UNITS blocks
We start the NMODL file with some
standard definitions useful in most channel membrane
mechanisms:
TITLE Calcium T channel for Subthalamic Nucleus
UNITS {
(mV) = (millivolt)
(mA) = (milliamp)
}
- The TITLE keyword allows us to identify what
this file is describing, though it is not required.
- The UNITS block defines more convenient aliases
for the the units that will be used in this file. By default,
NMODL understands units in the UNIX units database (see file
/usr/share/units.dat or look at the units
command on LINUX machines). It uses these units to check that
that equations are consistent. In the above example we are
telling NMODL that we want to use mV as a shorthand
for millivolt and mA as a shorthand for
milliamp.
The NEURON block
The NEURON block is the public interface of the
mechanism. It tells the hoc interpreter how
to refer to the mechanism and what variables it can see or
change. The structure of the block is as follows:
NEURON {
SUFFIX suffix
USEION ions... READ vars... WRITE vars...
RANGE var,var,...
GLOBAL var,var,...
}
The first step is to identify this mechanism from all other
membrane mechanisms when referencing it from the hoc language. This is done through the
SUFFIX statement of the block. Access to all variables
in this mechanism from the hoc file is then
done using the suffix. For example, we will call this channel
mechanism "CaT", so to access variables in the mechanism from
hoc we use var_CaT (where var
is a variable in this mechanism).
The USEION statement specifies what ions this
channel mechanism uses. There are three ions NEURON knows about, na, k,
ca, however, others may also be defined via this
statement. NEURON can keep track
of the intracellular and extracellular concentrations of each
ion. (Typically, these are actually concentrations in small
shells around either side of the membrane.) Dealing with ions
is difficult, because more than one mechanism may affect a
particular ion. For example, we may have more than one calcium
channel mechanism. Therefore, when dealing with ions use
exactly the same name used in all other mechanisms.
The READ modifier lists ionic variables needed in
calculating the ionic channel current (usually the equilibrium
potential, or concentration). The WRITE modifier lists
what ionic variables are calculated in this mechanism (usually
the current). In our example we use:
USEION ca READ eca WRITE ica
eca is the equilibrium potential for ion
ca, and ica is the calcium current, to be
calculated in this mechanism.
You probably expect that since we have just introduced
ica, a calcium current, NEURON
will automatically adjust the intra- and extracellular calcium
concentrations. It doesn't (though it can; the box contains more details.) One way to
think about this is that in this tutorial, we have deliberately
chosen not to model calcium accumulation adjacent to the
membrane, either intracellularly or extracellularly.
Note on how NEURON deals with
ions
NEURON does not change the calcium
concentrations automatically. To do this, we would
need another mechanism defined in an NMODL file that would WRITE cai and/or
cao, the intra- and extracellular calcium
concentrations. However this mechanism would need to know the
total calcium current ica originating from our CaT
mechanism and any other mechanisms affecting calcium current.
NEURON provides a means of doing this,
but it is outside the scope of this tutorial.
The RANGE statement makes the following variables
visible to the NEURON interpreter and
specifies that they are be functions of position. For example,
the maximum channel conductance should be a RANGE
variable, since it can be different at different points on a
neuron.
The GLOBAL statement specifies variables that are
always the same for the mechanism. This mechanism does not have
any GLOBAL variables. Our final NEURON block now has
the form:
NEURON {
SUFFIX CaT
USEION ca READ eca WRITE ica
RANGE gmax
}
We have called the maximum channel conductance variable
gmax.
The PARAMETER block
The PARAMETER block specifies variables that:
- are not changed as a result of the calculations in the
mechanism;
- are (generally) constant throughout time; and
- can be changed by the user from the hoc interface or the GUI.
We can see from the equation:
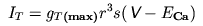
that in calculating this channel current our model will use
the voltage v, the maximum conductance we declared in
the NEURON block above, gmax and the calcium
equilibrium potential, eca. Of these only
gmax satisfies the conditions above; v is
calculated at every time step by NEURON
rather than being specified by the user, and eca may
also be calculated at each time step depending on the calcium
concentrations. The PARAMETER block is:
PARAMETER {
gmax = 0.002 (mho/cm2)
}
For each parameter, we specify the name of the parameter,
its default value and its units (in parentheses).
We change the value of gmax in a segment in which
CaT is inserted from hoc as follows:
soma gmax_CaT = 0.001
The ASSIGNED block
The ASSIGNED block declares variables that are either:
- calculated by the mechanism itself or
- computed by NEURON.
Variables that this mechanism will compute are the calcium
current ica, and variables for the rate equations
ralpha, rbeta, salpha etc. The
variables that the mechanism uses that are computed by NEURON are the membrane potential v
and the calcium equilibrium potential eca. The
ASSIGNED block is:
ASSIGNED {
v (mV)
eca (mV)
ica (mA/cm2)
ralpha (/ms)
rbeta (/ms)
salpha (/ms)
sbeta (/ms)
dalpha (/ms)
dbeta (/ms)
}
Note on equilibrium
potentials
As mentioned above eca is calculated by NEURON. How and when it is calculated depends on
the particular mechanisms dealing with ions that are inserted
in a section. In this tutorial, although there is a calcium
current ica, we have deliberately chosen not to
represent calcium accumulation adjacent to the membrane,
either intracellularly or extracellularly (see the Box: Note on how NEURON deals with ions). So in
our case NEURON use a built-in, i.e.
"default", eca. But NEURON's default
values for eca, ena, and ek are
not appropriate for our mammalian subthalamic nucleus. We
want to use typical mammalian values like the following (from
Johnston & Wu, 1999):
| Na |
K |
Ca |
| inside |
outside |
inside |
outside |
inside |
outside |
| 10 mM |
145 mM |
140 mM |
5 mM |
2e-4 mM |
2.5 mM |
| ena =
71.5 mV |
ek =
-89.1 mV |
eca =
126.1 mV |
where the equilibrium potentials ena,
ek, and eca are calculated at 37 degrees
Celsius according to the Nernst equation. We will set all of
these equilibrium potentials as our model has channels using
each of these ion species. These should be set after
the channel mechanisms are inserted into a section, and must
be set for each section that has channels using that ionic
species inserted. In our model, only the soma has such
channels. We can modify our SThcell template, adding
these equilibrium potential parameter values to the soma
block:
soma {
nseg = 1
diam = 18.8
L = 18.8
Ra = 123.0
insert hh
ena = 71.5
ek = -89.1
gnabar_hh=0.25
gl_hh = .0001666
el_hh = -60.0
insert CaT
eca = 126.1
}
Remember, if you insert channels into other sections, you
must modify the appropriate equilibrium potentials in that
section to make them consistent with the soma section.
The STATE block
The STATE block declares state variables. One type of state
variable are the variables that we are trying to solve for in
kinetic schemes. There are three state variables in our kinetic
channel model, r, s and d. The
STATE block is:
STATE {
r s d
}
The heart of the mechanism
We now come to the heart of the mechanism. We wish to
calculate the values of the variables r, s
and d in order to calculate the calcium current from
the above equation. These are given by the three kinetic
differential equations:
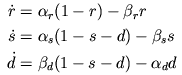
We must first calculate each of the functions
ralpha, rbeta, salpha,
sbeta, dalpha and dbeta. These
voltage dependent functions are specified by Wang et
al.. We can create a PROCEDURE to calculate these
functions. This allows us to calculate the equations at any
time by simply using our defined procedure. A procedure is
defined using the following format:
PROCEDURE name(vars) {
calculations...
}
In our case, we need a procedure that takes the current
voltage v and calculates values of the variables
ralpha, rbeta etc. We will call our procedure
settables. [Note the actual functions are taken from
Wang et al. (1991)]
PROCEDURE settables(v (mV)) {
LOCAL bd
ralpha = 1.0/(1.7+exp(-(v+28.2)/13.5))
rbeta = exp(-(v+63.0)/7.8)/(exp(-(v+28.8)/13.1)+1.7)
salpha = exp(-(v+160.3)/17.8)
sbeta = (sqrt(0.25+exp((v+83.5)/6.3))-0.5) *
(exp(-(v+160.3)/17.8))
bd = sqrt(0.25+exp((v+83.5)/6.3))
dalpha = (1.0+exp((v+37.4)/30.0))/(240.0*(0.5+bd))
dbeta = (bd-0.5)*dalpha
}
As these functions will need to be reevaluated at each time
step (as the voltage is changing), it is more computationally
efficient to create a table of values calculated at closely
spaced voltages at the start of a simulation, and use table
lookup with linear interpolation based on the current voltage
(memory is cheaper than computation). This can be done by
simply adding a TABLE line to the procedure. The
TABLE command has the form:
TABLE funcs DEPEND vars FROM lowest TO highest WITH steps
Where funcs, are the variables representing the
functions to create tables for (e.g. the alpha and beta
function variables) and vars are the variables, that if
they change value then all tables must be recalculated. In our
case, lowest and highest are the lowest and
highest values of the voltage we make the tables over, with
steps steps between them. Our procedure now looks
like:
PROCEDURE settables(v (mV)) {
LOCAL bd
TABLE ralpha, rbeta, salpha, sbeta, dalpha, dbeta
FROM -100 TO 100 WITH 200
ralpha = 1.0/(1.7+exp(-(v+28.2)/13.5))
rbeta = exp(-(v+63.0)/7.8)/(exp(-(v+28.8)/13.1)+1.7)
salpha = exp(-(v+160.3)/17.8)
sbeta = (sqrt(0.25+exp((v+83.5)/6.3))-0.5) *
(exp(-(v+160.3)/17.8))
bd = sqrt(0.25+exp((v+83.5)/6.3))
dalpha = (1.0+exp((v+37.4)/30.0))/(240.0*(0.5+bd))
dbeta = (bd-0.5)*dalpha
}
Now, to calculate all the alpha and beta functions we simply
call the procedure settables. The alpha and beta
functions are used by our differential equations:
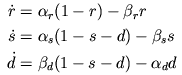
These equations can be directly specified in a
DERIVATIVE block. The DERIVATIVE block
requires a name, and we will call ours states.
DERIVATIVE states {
settables(v)
r' = ((ralpha*(1-r)) - (rbeta*r))
d' = ((dbeta*(1-s-d)) - (dalpha*d))
s' = ((salpha*(1-s-d)) - (sbeta*s))
}
Each time NEURON calculates the
differential equations, the alpha and beta variables must be
updated, so the first line calls our procedure
settables with the current voltage v. Then
each differential equation is specified.
Our BREAKPOINT is the top level mechanism
calculation block that simply solves the differential equations
and calculates the calcium current.
BREAKPOINT {
SOLVE states METHOD cnexp
ica = gmax*r*r*r*s*(v-eca)
}
The current is calculated directly from the equation:
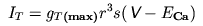
The SOLVE statement refers to the states
defined in our DERIVATIVE block. The METHOD
cnexp part of the line tells NEURON to
use the "cnexp" method of integration. This method is suitable
for mechanisms of the form
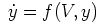
where f is linear in y and involves no other states.
Hodgkin-Huxley-type equations fall into this category.
The final block we must specify is the INITIAL
block. This block is used to set the state variables
r, d and s to to their initial
values. Usually these are the values of the state variables at
equilibrium. The INITIAL block first calls the
procedure settables with the present voltage to
calculate the values of the alpha and beta functions. These in
turn are then used to calculate the initial state variables.
The INITIAL block is:
INITIAL {
settables(v)
r = ralpha/(ralpha+rbeta)
s = (salpha*(dbeta+dalpha) - (salpha*dbeta))/
((salpha+sbeta)*(dalpha+dbeta) - (salpha*dbeta))
d = (dbeta*(salpha+sbeta) - (salpha*dbeta))/
((salpha+sbeta)*(dalpha+dbeta) - (salpha*dbeta))
}
Note the values for r, d and s
are derived from the differential equations at equilibrium.
Putting it all together
The final and complete NMODL
specification for the low threshold calcium T-type channel is
given in the file CaT.mod and is listed below.
TITLE Calcium T channel for Subthalamic Nucleus
UNITS {
(mV) = (millivolt)
(mA) = (milliamp)
}
NEURON {
SUFFIX CaT
USEION ca READ eca WRITE ica
RANGE gmax
}
PARAMETER {
gmax = 0.002 (mho/cm2)
}
ASSIGNED {
v (mV)
eca (mV)
ica (mA/cm2)
ralpha (/ms)
rbeta (/ms)
salpha (/ms)
sbeta (/ms)
dalpha (/ms)
dbeta (/ms)
}
STATE {
r s d
}
BREAKPOINT {
SOLVE states METHOD cnexp
ica = gmax*r*r*r*s*(v-eca)
}
INITIAL {
settables(v)
r = ralpha/(ralpha+rbeta)
s = (salpha*(dbeta+dalpha) - (salpha*dbeta))/
((salpha+sbeta)*(dalpha+dbeta) - (salpha*dbeta))
d = (dbeta*(salpha+sbeta) - (salpha*dbeta))/
((salpha+sbeta)*(dalpha+dbeta) - (salpha*dbeta))
}
DERIVATIVE states {
settables(v)
r' = ((ralpha*(1-r)) - (rbeta*r))
d' = ((dbeta*(1-s-d)) - (dalpha*d))
s' = ((salpha*(1-s-d)) - (sbeta*s))
}
UNITSOFF
PROCEDURE settables(v (mV)) {
LOCAL bd
TABLE ralpha, rbeta, salpha, sbeta, dalpha, dbeta
FROM -100 TO 100 WITH 200
ralpha = 1.0/(1.7+exp(-(v+28.2)/13.5))
rbeta = exp(-(v+63.0)/7.8)/(exp(-(v+28.8)/13.1)+1.7)
salpha = exp(-(v+160.3)/17.8)
sbeta = (sqrt(0.25+exp((v+83.5)/6.3))-0.5) *
(exp(-(v+160.3)/17.8))
bd = sqrt(0.25+exp((v+83.5)/6.3))
dalpha = (1.0+exp((v+37.4)/30.0))/(240.0*(0.5+bd))
dbeta = (bd-0.5)*dalpha
}
UNITSON
One final note, you may notice the commands UNITSON
and UNITSOFF in the file. These activate the units
checking (e.g. mV, mA etc.) and deactivate it respectively.
Now if we inject a hyperpolarising current in one of our
neurons, we now observe a post-hyperpolarising T-type
response:
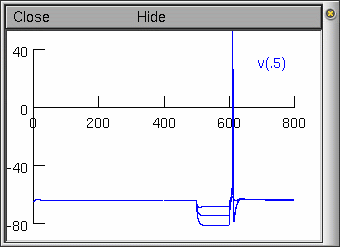
With current injections at -0.1, -0.2, and -0.3 nA.
Note: The action potential is unrealistic for
mammalian subthalamic cells (it is still based on our HH squid
axon channels). We leave it to the reader to go on and develop
channels to underlie an action potential more characteristic of
the mammalian subthalamic projection neuron.
In part E of this tutorial, we will
look at ways of getting data out of neuron, and methods of speeding
up simulations.
References
Hines, M. L. and Carnevale, N. T. (2000)
"Expanding NEURON's repertoire of mechanisms with NMODL"
Neural Computation 12: 839-851
Johnston, D. and Wu, S. (1995) Foundations
of Cellular Neurophysiology. MIT Press, Cambridge,
Massachusetts.
Wang, X., Rinzel, J. and Rogawski, M. (1992) "A
model of the T--type calcium current and the low threshold
spike in thalamic neurons". J. Neurophys.
66: 839-850
Andrew Gillies (andrew@anc.ed.ac.uk)
David Sterratt (dcs@anc.ed.ac.uk)
with the assistance of Ted Carnevale and Michael Hines
Last modified on
 An important
electrophysiological feature of subthalamic neurons is the post
hyperpolarising response. When a neuron is hyperpolarised (e.g.
by current injection or inhibitory synaptic input), at the end
of the hyperpolarisation, a burst of activity is observed in
subthalamic projection neurons (see left). This response is
mediated by a low threshold calcium selective ion channel,
called the T-type calcium channel.
An important
electrophysiological feature of subthalamic neurons is the post
hyperpolarising response. When a neuron is hyperpolarised (e.g.
by current injection or inhibitory synaptic input), at the end
of the hyperpolarisation, a burst of activity is observed in
subthalamic projection neurons (see left). This response is
mediated by a low threshold calcium selective ion channel,
called the T-type calcium channel.